Теоретические сведения

В авиационных газотурбинных двигателях (ГТД) ротор представляет собой сложную конструкцию, состоящую из барабанно-дисковых элементов компрессора и турбины, собственно вала и цапф.

При работе двигателя вал испытывает нагрузки, приводящие к возникновению деформаций кручения, изгиба, растяжения и сжатия. Кроме того, на статические напряжения накладываются напряжения, возникающие вследствие динамического нагружения, возникающего в результате действия периодических сил, вызываемых неравномерностью газового потока и/или дисбалансом ротора данного ГТД. По мере приближения к критической частоте вращения прогиб ротора непрерывно и быстро увеличивается, вследствие чего лопатки ротора могут задевать корпус двигателя.

Величину критических оборотов можно определить, рассмотрев модель простейшего ротора, состоящего из вала и одного диска с массой (рис. 6).

 

Рис. 6. Изменение прогиба вала в связи с изменением частоты (угловой скорости) вращения ротора

 

При вращении центробежная сила, действующая на диск ротора, равна

(4)

где у - прогиб вала; е - эксцентриситет центра масс диска; - угловая скорость вращения ротора.

На установившихся оборотах центробежная сила равна силе упругого противодействия (у. п.) вала, то есть:

(5)

где с - изгибная жесткость ротора.

Решая совместно уравнения (4) и (5), можно установить связь между прогибом ротора у и угловой скоростью:

(6)

При равенстве квадрата угловой скорости величине знаменатель в уравнении (6) превращается в нуль, а прогиб у стремится к бесконечности.

Угловая скорость, при которой ее квадрат равен , называется критической угловой скоростью , то есть:

(7)

Критические обороты ротора п_кр соответственно будут равны:

(8)

Подставляя в подкоренное выражение вместо массы диска его вес , получаем:

(9)

Из уравнения (6) следует, что при частоте вращения ротора, отличной от критической, прогиб может быть положительным (при ) и отрицательным (при .

В первом случае (см. рис. 6) роторы, работающие с частотой вращения меньше критической, называются «жесткими», а роторы, работающие в закритической зоне, - «гибкими».

В обоих случаях на достаточном удалении квадрата угловой скорости от величины прогибы малы, поэтому могут эксплуатироваться как «жесткие», так и «гибкие» роторы.

При гибком роторе (рис. 7,б) центр массы ротора расположен между прямой АОВ и кривой АО₁В. В данном случае по мере увеличения частоты вращения в закритической зоне прогиб ротора уменьшается и стремится к величине е.

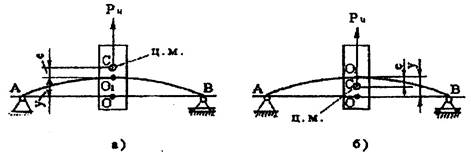
Рис. 7. Положение элементов роторов при их вращении: а) «жесткий ротор»; б) «гибкий ротор»

 

Критическую частоту вращения ротора простейшей однодисковой схемы можно определить аналитически. Задачу по определению критической частоты вращения многодискового ротора можно решить методом разложения сложной схемы ротора на простейшие с одним диском (рис. 8). Раздельно определяют критическую частоту вращения одного вала ротора без дисков (поз. б), затем каждого диска в отдельности (поз. в, г, д) по формуле (5 или 6), считая при этом вал невесомым.

Рис. 8. Схема расчета: а) сложного ротора с тремя дисками; б) вал без дисков; в), г), д) невесомый вал и диск массой

Критическую частоту вращения вала без дисков определяют по формуле:

(10)

где Е - модуль упругости материала; J - момент инерции сечения вала (для сплошного вала с диаметром d, J = 0,05d); т_в - масса единицы длины вала.

Жесткость ротора с зависит от размеров вала, места приложения нагрузки, условий размещения вала на опорах и материала, из которого ротор сделан.

При определении значений критических оборотов по формуле (6) в зависимости от расположения диска (рис. 9) рассчитывают по формулам применительно к соответствующей схеме расположения диска:

а) (11)

б) (12)

в) (13)

Рис. 9.Роторы с различным расположением дисков: а) посередине; б) вблизи одной из опор; в) на консоли

 

Критическая частота вращения сложного ротора (см. рис. 7) определяется по суммирующей формуле:

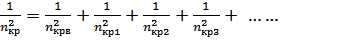(14)

При критических частотах вращения роторов проявляется явление прецессии. Если вал с диском, расположенным консольно (см. рис. 4, в; 5), вращающийся с угловой скоростью прогнется на величину у, и консоль повернется на угол , то вал с диском будут вращаться вокруг касательной оси ОО₁. Прогнувшийся вал с диском может вращаться вокруг оси ОО. Угловая скорость этого вращения 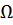в общем случае отличается от угловой скорости . Направление вращения может совпадать с угловой скоростью или быть ей противоположной. В первом случае это прямая прецессия, во втором - обратная (Рис. 10).

Рис. 10. Движение вала с консольно расположенным диском при явлении прецессии: а) прямая прецессия; б) обратная прецессия

 

При частоте вращения, отличающейся от критической, прогиб вала зависит от величины дисбаланса ротора.