Метод Эйлера

Пусть для отрезка [a, b], на котором ищется решение дифференциального уравнения (2.1), построена сеточная область 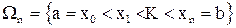с постоянным шагом h. Для построения решения уравнения (2.1) воспользуемся разложением искомой функции y(x) в ряд Тэйлора вблизи произвольной точки :

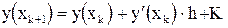
Учитывая, что согласно уравнению (2.1) , это разложение решения можно записать в виде

С помощью полученного выражения построим вычислительный процесс

. (2.6)

Здесь и далее будем обозначать символами результат численного решения уравнения (2.1), а выражение будем использовать для обозначения точного решения исходной задачи.

Пример 2.3. Решим методом Эйлера уравнение .

В этом частном случае правая часть дифференциального уравнения имеет вид , то есть схема (2.6) записывается следующим образом:

Построим последовательность значений искомой функции для узлов сетки :

, ...,

Для оценки точности получаемого численного решения производятся вычисления с различными шагами интегрирования h (табл. 2.1). Точное решение , например, для x=10 дает значение y(10)=0,4539992976·10^-4.

Таблица 2.1.

Результаты численного решения y_n методом Эйлера обыкновенного дифференциального уравнения с начальным условием y(0)=1.

Величина шага h	0.5	0.25	0.1	0.01	0.001	0.0001
Число шагов n
y_n·10^-4.	0,009537	0,100566	0,265614	0,431713	0,451733	0,453772

Верные три значащие цифры получены для шага h = 0,0001, при этом требуется выполнить 100000 “шагов” по аргументу x, то есть выполнить вычислений в соответствии с формулой (2.6).

Для оценки точности решения, как и ранее, представим погрешность в виде

определяющем отклонение численного решения по схеме Эйлера от точного.

Соотношение (2.6) запишем в виде разностного аналога дифференциального уравнения (2.1):

. (2.7)

Подставляя в выражение (2.7) и , получаем

Преобразуем последнюю формулу, добавляя в правую часть и одновременно вычитая ,

(2.8)

Выражение в квадратных скобках представляет собой разностный аналог (2.7), в котором приближенные значения y_k искомой функции заменены на точные значения y(x_k). Это позволяет проверить, как точно разностный аналог (2.7) аппроксимирует исходное дифференциальное уравнение (2.1).

Величина

(2.9)

носит название погрешности аппроксимации исходного дифференциального уравнения разностным аналогом. Для оценки этой погрешности подставим разложение решения в ряд Тэйлора

в формулу (2.9):

Учтем, что согласно исходному уравнению . Тогда

При условии, что значения ограничены на отрезке [a, b], погрешность аппроксимации оказывается величиной, пропорциональной первому порядку шага интегрирования.

В общем случае порядок аппроксимации равен p, если имеет место соотношение вида

Вновь обратимся к формуле (2.8). Второе слагаемое согласно теореме Лагранжа о среднем можно представить в виде:

Тогда выражение (2.8) преобразуется следующим образом:

Для того, чтобы при выполнении вычислений погрешность не возрастала, потребуем выполнения условия:

. (2.10)

Полученное неравенство соответствует критерию устойчивости по начальным данным, , полученному ранее. Далее, с учетом выполнения условия Липшица , оценим производную

Учитывая условие устойчивости решения, , получаем:

Теперь из неравенства (2.10) можно получить:

Следовательно, чтобы не нарастала погрешность вычислений, необходимо ограничивать величину шага интегрирования.

[1] Очевидно, что граничная задача может быть сформулирована лишь для дифференциальных уравнений второго и более высокого порядков.

[2] Под устойчивостью в данном случае понимается непрерывная зависимость решения от входных данных, [2].

[3] Пеано Джузеппе [27.8.1858 - 20.9.1930] - итальянский математик. С 1890 года - профессор Туринского университета.

[4] Пикар Шарль Эмиль [24.7.1856 - 11.12.1941] - французский математик. В 1877 году окончил Высшую нормальную школу в Париже. С 1881 года - професор этой же школы, а с 1886 года - профессор Парижского университета. С 1895 член-корреспондент Петербургской академии наук; с 1889 - член Парижской академии наук; с 1924 года - член Французской академии наук; с 1925 года - почетный член академии наук СССР.