Экзаменационный тест по дисциплине «Методы оптимальных решений»
| № | Содержание вопроса | Варианты ответа | ||||||||||||||||||||||||
| Задача об использовании ресурсов сформулирована полностью и имеет общий вид: | 1. 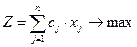 при ограничениях
при ограничениях
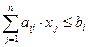 , , 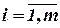 ; ;
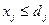 , , 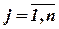 ; ;
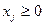 , , 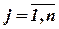 .
2. .
2. 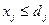 , , 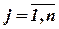 3.
3. 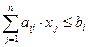 4.
4. 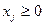 . .
| |||||||||||||||||||||||||
| Модель Леонтьева имеет вид: | 1. 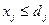 2.
2. 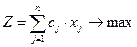 3.
3. 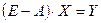 4.
4. 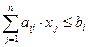
| |||||||||||||||||||||||||
| Методы динамического программирования применяются для | 1. если балансовое соотношение может записано в следующем матричном виде:
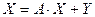 .
2. повышения эффективности вычислений при решении задач математического программирования путем их разложения (декомпозиции) на менее сложные подзадачи;
3. для оптимального решения задачи линейного программирования;
4. для выявления недефицитных ограничений. .
2. повышения эффективности вычислений при решении задач математического программирования путем их разложения (декомпозиции) на менее сложные подзадачи;
3. для оптимального решения задачи линейного программирования;
4. для выявления недефицитных ограничений.
| |||||||||||||||||||||||||
| Принцип оптимальности Беллмана: | 1. Каковы бы ни были предыдущее состояние и принятое предыдущее решение, последующие решения должны составлять оптимальную стратегию относительно состояния, возникшего в результате предыдущего решения; 2. Каковы бы ни настоящее решение, последующие решения должны составлять оптимальную стратегию относительно состояния, возникшего в результате настоящего решения; 3. Каковы бы ни были будущее состояние и будущее решение, предыдущие решения должны составлять оптимальную стратегию относительно состояния, возникшего в результате будущего решения; 4. Нет правильного ответа. | |||||||||||||||||||||||||
| Уравнением Беллмана называется рекуррентное соотношение представленное в виде: | 1. 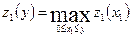 2.
2. 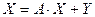 3.
3. 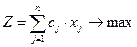 4.
4. 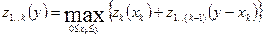 .
.
| |||||||||||||||||||||||||
| Задача рентабельности затрат на производство изделий имеет вид: | 1. 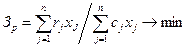 2.
2. 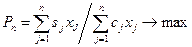 .
3. .
3. 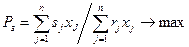 .
4. нет правильного ответа. .
4. нет правильного ответа.
| |||||||||||||||||||||||||
| Задача рентабельности продаж имеет вид: | 1. 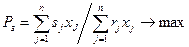 2.
2. 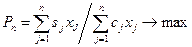 3.
3. 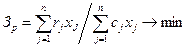 4. нет правильного ответа.
4. нет правильного ответа.
| |||||||||||||||||||||||||
| Функцию Лагранжа имеет вид: | 1. 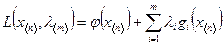 .
2. .
2. 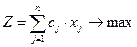 3.
3. 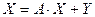 4.
4. 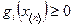 , , 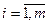
| |||||||||||||||||||||||||
| Неравенство ______________ называется теоремой Куна-Таккера: | 1. 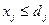 2.
2. 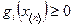 3.
3. 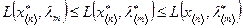 4.
4. 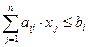 . .
| |||||||||||||||||||||||||
| Универсальный метод решения задач линейного программирования – это | 1. симплексный метод 2.метод динамического программирования 3. уравнение Леонтьева 4. метод множителей Лагранжа. | |||||||||||||||||||||||||
| Выявление недефицитных ограничений в задаче об использовании ресурсов позволяет | 1. повысить спрос над предложением 2. прогнозировать или определять полученные заказы 3. выявить доход от реализации выпускаемой продукции 4. уменьшить запас имеющихся ресурсов, а следовательно, снизить расходы на их приобретение и хранение | |||||||||||||||||||||||||
| Коэффициенты прямых материальных производственных затрат определяют | 1. стоимость части продукции j-ой отрасли, непосредственно затрачиваемой в качестве предметов труда на выпуск единицы стоимости продукции i-ой отрасли
2. стоимость части продукции j-ой отрасли, непосредственно затрачиваемой в качестве предметов труда на выпуск единицы стоимости продукции i-ой отрасли
3. что нужно воспользоваться в качестве производственного потребления частью валового продукта 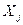 4. нет правильного ответа.
4. нет правильного ответа.
| |||||||||||||||||||||||||
| Коэффициенты полных материальных затрат определяют | 1. стоимость части продукции j-ой отрасли, непосредственно затрачиваемой в качестве предметов труда на выпуск единицы стоимости продукции i-ой отрасли
2. стоимость части продукции j-ой отрасли, непосредственно затрачиваемой в качестве предметов труда на выпуск единицы стоимости продукции i-ой отрасли
3. что нужно воспользоваться в качестве производственного потребления частью валового продукта 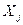 4. нет правильного ответа.
4. нет правильного ответа.
| |||||||||||||||||||||||||
| Экстремум функции | 1. (6,4)
2.(2,3; 7,7)
3. (5;4)
4. 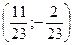
| |||||||||||||||||||||||||
Условный экстремум функции 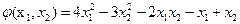 при условии (ограничении)
при условии (ограничении) 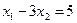 равен равен
| 1.13 2.-13 3.11 4.-11. | |||||||||||||||||||||||||
Для реконструкции трех заводов выделено 5 млн. руб. капиталовложений. Увеличение выпуска продукции (в млн. руб.) после реконструкции в зависимости от выделенного i-ому заводу 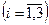 объема капиталовложений x обозначим объема капиталовложений x обозначим 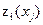 и зададим в таблице: и зададим в таблице:
Распределения капиталовложений | 1. 34 2. 45 3. 33 4. 44. | |||||||||||||||||||||||||
| Экономика включает две главные подсистемы | 1. производственную и финансово-кредитную 2. социальную и оборонную 3. моральную и политическую 4. нет правильного ответа. | |||||||||||||||||||||||||
| В совокупности валовые капитальные вложения и непроизводственное потребление представляют собой | 1. производственное потребление 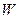 2. валового продукта
2. валового продукта 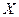 3. конечный продукт
3. конечный продукт 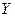 4. Валовые капитальные вложения
4. Валовые капитальные вложения 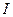 . .
| |||||||||||||||||||||||||
| Валовые капитальные вложения разделяются на | 1. на валовые капитальные вложения I (инвестиции) и на непроизводственное потребление C 2. амортизационные отчисления A и на чистые капитальные вложения V 3. на конечный продукт Y и производственное потребление W 4. нет правильного ответа. | |||||||||||||||||||||||||
| Чистые капитальные вложения и прирост основных производственных фондов описываются уравнением | 1. 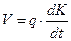 2.
2. 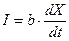 3.
3. 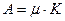 4.
4. 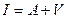 . .
| |||||||||||||||||||||||||
| Прирост валового продукта через валовые капитальные вложения описывается уравнением | 1. 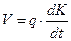 2.
2. 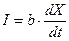 3.
3. 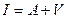 4.
4. 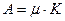 . .
| |||||||||||||||||||||||||
| Уравнение, связывающее между собой функции состояния и управления называется | 1. основным уравнением 2. целевым функционалом 3. уравнением движения 4.уравнением Беллмана. | |||||||||||||||||||||||||
| Уравнение движения имеет вид | 1. 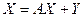 2.
2. 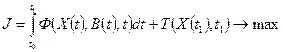 3.
3. 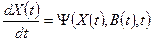 4.
4. 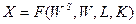
| |||||||||||||||||||||||||
| Состояние экономики в задаче оптимального управления развитием экономики выражается формулой | 1. 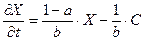 2.
2. 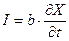 3.
3. 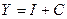 4.
4. 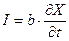 . .
| |||||||||||||||||||||||||
| Управление в задаче оптимального управления развитием экономики управление выражается функцией | 1. 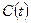 2.
2. 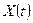 3.
3. 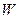 4.
4. 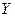 . .
|
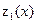
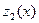
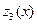
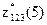 , при котором суммарное увеличение выпуска продукции на трех заводах максимально равно
, при котором суммарное увеличение выпуска продукции на трех заводах максимально равно