Виды дисперсий и правило сложения дисперсий.

Если данные представлены в виде аналитической группировки (выявляющая взаимосвязи между изучаемыми явлениями и их признаками взаимосвязь между признаком-фактором и признаком-результатом), то можно вычислить дисперсию общую, межгрупповую и внутригрупповую.

Общая дисперсия измеряет вариацию признака во всей совокупности под влиянием всех факторов, обуславливающих эту вариацию. σ²=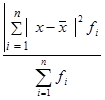

Межгрупповая дисперсия отражает вариацию изучаемого признака, которая возникает под влиянием признака-фактора, положенного в основу группировки. Она характеризует колеблемость групповых средних 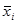около общей средней х₀. Она вычисляется по формуле:

где к-число групп;

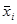– средняя по отдельным группам;

- общая средняя по совокупности единиц;

f_i -численность по отдельной группе.

Внутригрупповая дисперсия – отражает случайную вариацию, возникающую под действием других, неучиваемых факторов и не зависит от признака фактора положенного в основание группировки. Она исчисляется следующим образом:

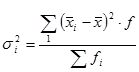
Средняя из внутригрупповых дисперсий:

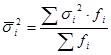
Существует закон, связывающий три вида дисперсий. Общая дисперсия равна сумме средней из внутригрупповых и межгрупповых дисперсий:

. Данное соотношение называют правилом сложения дисперсий. Согласно этому правилу общая дисперсия, возникающая под действием всех факторов, равна сумме дисперсий, возникающих под влиянием всех прочих факторов, и дисперсии, возникающей за счет группировочного признака.

Например, Имеются данные распределения торговых предприятий по объему прибыли и формам собственности. Необходимо определить дисперсии.

Объем прибыли в среднем на одно предприятие :

=181,4/100=1,814 млн. руб.

Общая дисперсия равна: 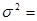8,9004/100=0,089804 млрд. руб.

Объем прибыли в среднем на одно государственное предприятие составил:

=100/50=2,0 млрд. руб.;

=2,34/50=0,0468 млрд. руб., Таким образом, 46,8 млн. руб. характеризуют вариацию признака внутри группы государственных предприятий.

Среднюю и дисперсию по негосударственным предприятиям определим используя свойство средней и дисперсии по способу моментов:

Тогда средний объем прибыли на одно предприятие составит: m₁=-18/50=-0,36; m₂=86/50=1,72

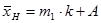=(-0,36)*0,2+1,7=1,628 млрд. руб.,

где в качестве А принимается одна из центральных вариант ряда (А=1,7).

=к²(m₂-m₁²)=0,2(1,72-(-0,36)²)=0,063616 млрд. руб.

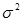=(46,8+63,616)/2=55,208 млн. руб.

Рассчитаем межгрупповую дисперсию по формуле:

=3,4596/100=0,034596 млрд. руб.

Группы магазинов по формам собственности	Средний объем прибыли одного предприятия	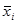Число предприятий f	( )	( )²	( )²f
Магазины государственные	2,0		0,186	0,034596	1,7298
Магазины негосударственные	1,628		-0,186	0,034596	1,7298
Итого	-		-	-	3,4596

Общая дисперсия равна =34,596+55,208=89,804 млн. руб.

Закон сложения дисперсий позволяет вычислить эмпирическое корреляционное отношение (коэффициент детерминации):

=34,596/89,804=38,5

Следовательно, 38,5 % различий в объеме прибыли предприятий обусловлены формой собственности предприятий и 61,5 % -влиянием других факторов.