Гармонические колебания.

Гармонические колебания представляют собой периодический процесс, в котором изменение величины происходит по закону косинуса (или синуса). Например, проекция радиуса-вектора точки, движущейся по окружности, на ось , лежащую в плоскости движения точки (рис.2), изменяется со временем по косинусоидальному закону. Если окружность имеет радиус , а угловая скорость вращения точки постоянна, то проекция

Период изменения , очевидно, будет равен , где – время одного оборота точки, через которое весь процесс в точности повторяется; w – циклическая (круговая) частота; – начальный угол поворота относительно оси . Следовательно, w отличается множителем 2p от частоты n:

Так как максимальное значение косинуса равно единице, то максимальное значение равно . Это максимальное значение называется амплитудой колебаний.

Аргумент косинуса носит название фазы колебаний, а - начальной фазы колебаний.

Пусть теперь гармонические колебания вдоль оси совершает материальная точка массой . Выясним, какая при этих условиях на нее должна действовать сила.

Проекция скорости точки на ось

,

проекция ускорения

По второму закону Ньютона

где - постоянный коэффициент.

Таким образом, для того чтобы материальная точка совершала гармонические колебания, действующая на нее сила должна быть пропорциональна и направлена в сторону, противоположную смещению . Такая сила называется упругой (или в общем случае - квазиупругой).

Рассмотрим систему, состоящую из груза массой , подвешенного на пружине, массой которой можно пренебречь (рис.3). Пусть - длина пружины без подвешенного к ней груза, тогда под тяжестью груза пружина растянется на . В положении равновесия модуль силы тяжести равен модулю упругой силы : , где - коэффициент упругости пружины.

Если вывести груз из положения равновесия 0, то на груз будет действовать дополнительная сила упругости, проекция которой на направленную вниз ось будет равна (закон Гука). Под действием этой силы груз, после смещения на и предоставленный самому себе, будет совершать гармонические колебания. Основное уравнение динамики поступательного движения (второй закон Ньютона) для груза принимает вид

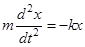(4)

Решение этого уравнения имеет вид

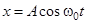(5)

Функция (5) - это закон движения груза на пружине, где - амплитуда колебания, т.е. наибольшее отклонение груза от положения равновесия. Подставляя решение (5) в (4), получаем

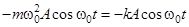
Отсюда собственная частота системы

Так как 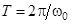, то

В рассмотренном примере не учитывалась сила сопротивления, поэтому колебания считались незатухающими.