Глоссарий

Эконометрика –это наука, которая даёт количественное выражение взаимосвязей экономических явлений и процессов.

Эконометрические модели позволяют выявить особенности функционирования экономического объекта и на основе этого предсказывать будущее его поведение при изменении каких-либо параметров.

Эндогенные – это внутренние переменные получаются в результате расчетов (например, выпуск продукции, численность работников, производительность труда)

Экзогенные - внешние переменные (например, поставка ресурсов, климатические условия и др.), задаются вне модели, т.е. известны заранее, а эндогенные переменные.

Регрессионными называют модели, основанные на уравнении регрессии, или системе регрессионных уравнений, связывающих величины эндогенных (у) и экзогенных (х) переменных.

Линейная модель уравнение парной регрессии имеет вид:

у = а₀ + а,х,

Линейная модель уравнение множественной регрессии:

у = а₀+а,х,+а₂х₂₊.. а_nх_n

Функциональные связи характеризуются полным соответствием между изменением факторного признака (признаков) и исследуемого показателя. Так, величина начисленной зарплаты при повременной оплате труда однозначно определяется количеством отработанных часов.

Корреляционные связи характеризуются тем, что между изменением факторного и результативного признаков нет однозначного соответствия, воздействие факторов проявляется лишь в среднем при многократном наблюдении фактических данных.

Парная регрессия– регрессия между двумя переменными y и x, то есть модель вида: y=f(x)+ε, где:

y - зависимая переменная (результативный признак),

x – независимая, объясняющая, переменная ( признак- фактор),

ε - возмущение или стохастическая переменная, включающая влияние неучтенных в модели факторов.

Метод наименьших квадратов –метод оценивания параметров линейной регрессии, минимизирующий сумму квадратов отклонений наблюдений зависимой переменной от искомой линейной функции.

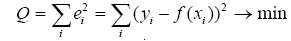
Коэффициент корреляции величин x и y (r_xy)– свидетельствует о наличии или отсутствии линейной связи между переменными:

Если: r_xy = -1, то наблюдается строгая отрицательная связь;

r_xy = 1, то наблюдается строгая положительная связь;

r_xy = 0, то линейная связь отсутствует.

Коэффициент детерминации (r_xy²)– характеризует долю дисперсии результативного признака y, объясняемую дисперсией, в общей дисперсии результативного признака. Чем ближе r_xy² к 1, тем качественнее регрессионная модель, то есть исходная модель хорошо аппроксимирует исходные данные.

Временной ряд - это последовательность экономических показателей измеренных через равные промежутки времени. В экономике временные ряды - это ежедневные цены на акции, курсы валют, еженедельные и месячные объемы продаж, годовые объемы производства и т.п.

Трендом временного ряда называют плавно изменяющуюся, не циклическую компоненту, описывающую чистое влияние долговременных факторов, эффект которых сказывается постепенно.

Сезонная компонента временного ряда отражает повторяемость процессов во времени. Описывает поведение, изменяющееся регулярно в течение заданного периода (года, месяца, недели, дня и т.п.). Она состоит из последовательности почти повторяющихся циклов.

Циклическая компонента занимает как бы промежуточное положение между закономерной и случайной составляющими временного ряда, описывает длительные периоды относительного подъёма и спада.

Мультиколлинеарность наличие среди переменных (факторов) линейно связанных.

Коллинеарность - линейная зависимость, если парный коэффициент корреляции между ними по абсолютной величине превышает 0,8.

Коэффициент детерминации применяется для оценки тесноты связи модели с исходными данными, показывает долю изменения (вариации) результативного признака под действием факторного признака.

Коэффициент эластичности показывает, на сколько процентов изменяется результативный признак у при изменении факторного признака X, на один процент.

Аддитивная модель – модель вида: Y=T+S+E,

где Т - трендовая компонента;

S – циклическая компонента;

Е – случайная компонента.

Мультипликативная модель – модель вида: Y=T*S*E.

Автокорреляция временного ряда – корреляционная зависимость между последовательными уровнями временного ряда.

Лаг – число периодов, по которым рассчитывается коэффициент автокорреляции.

Две переменные явно коллинеарны, т. е. находятся между собой в линейной зависимости, если r_xixj ≥ 0,7

Общая сумма квадратов отклонений (S_общ):

Факторная сумма квадратов отклонений (S_факт):

Остаточная сумма квадратов отклонений (S _ост):

S _ост= S_общ - S_факт.

Дисперсия на одну степень свободы:

Д_общ = S_общ /(n-1); Д_фак= S_фак / 1; Д_ост = S _ост/ (n-2).

F – критерий Фишера:

F_выч=Д_фак / Д_ост.

Если F_выч>F_таб, то уравнение регрессии значимо.

Стандартные ошибки коэффициентов регрессии:

Фактическое значение t-критерия Стьюдента:

t_b=b/m_b; t_a=a/m_a.

Доверительные интервалы :b+t* m_b и b-t* m_b; a+t* m_a и a-t* m_a.

Корреляция для нелинейной регрессии:

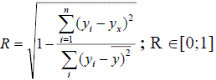
Чем ближе R к 1, тем теснее связь рассматриваемых признаков.

F-критерий Фишера для нелинейной регрессии:

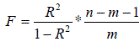
где: n – число наблюдений, а m – число параметров при переменных x.

Средняя ошибка аппроксимации:

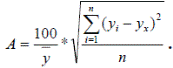
Гомоскедастичность дисперсии остатков означает, что для каждого значения фактора x_j остатки (ε = y_{i - i)} имеют одинаковую дисперсию. (Это условие применения МНК).

Гетероскедастичностьдисперсии остатков означает, что для каждого значения фактора x_j остатки ε различны, не имеют одинаковую дисперсию, выполняются неравенства