Проверка статистических гипотез
2.4.1. В таблице даны результаты 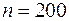 наблюдений над случайной величиной
наблюдений над случайной величиной 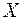 :
:
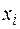
| 0,3 | 0,5 | 0,7 | 0,9 | 1,1 | 1,3 | 1,5 | 1,7 | 1,9 | 2,1 | 2,3 |
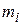
|
Проверить, используя критерий  Пирсона, согласуются ли эти данные с гипотезой о нормальном
Пирсона, согласуются ли эти данные с гипотезой о нормальном  распределении генеральной совокупности. Уровень значимости принять равным
распределении генеральной совокупности. Уровень значимости принять равным  .
.
2.4.2. Используя критерий  при уровне значимости
при уровне значимости  проверить, согласуется ли следующая выборка, представленная в виде статистического ряда, с гипотезой о нормальном распределении генеральной совокупности.
проверить, согласуется ли следующая выборка, представленная в виде статистического ряда, с гипотезой о нормальном распределении генеральной совокупности.
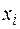
| |||||||||
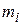
|
2.4.3. Используя критерий  , проверить при уровне значимости
, проверить при уровне значимости  , согласуются ли с гипотезой о нормальном распределении генеральной совокупности следующие данные, представленные в виде интервального статистического ряда:
, согласуются ли с гипотезой о нормальном распределении генеральной совокупности следующие данные, представленные в виде интервального статистического ряда:
| Номер интервала k | Границы интервала 
| Частота интервала 
|
| 3 – 8 8 – 13 13 – 18 18 – 23 23 – 28 28 – 33 33 – 38 |
2.4.4. В итоге регистрации времени прихода 800 посетителей выставки (в качестве начала отсчета времени принят момент открытия работы выставки) получены данные представленные в следующей таблице:

| 
| 
| 
|
| 0 – 1 | 4 – 5 | ||
| 1 – 2 | 5 – 6 | ||
| 2 – 3 | 6 – 7 | ||
| 3 – 4 | 7 – 8 |
где  - интервалы времени;
- интервалы времени;  - частоты интервалов, т.е. количество посетителей, пришедших в течение соответствующего интервала. Требуется при уровне значимости
- частоты интервалов, т.е. количество посетителей, пришедших в течение соответствующего интервала. Требуется при уровне значимости  проверить гипотезу о том, что время прихода посетителей выставки распределено по показательному закону с параметром
проверить гипотезу о том, что время прихода посетителей выставки распределено по показательному закону с параметром  .
.
2.4.5. Испытания 200 элементов на продолжительность работы дали результаты, приведенные в следующей таблице:

| 
| 
| 
|
| 0 – 5 | 15 – 20 | ||
| 5 – 10 | 20 – 25 | ||
| 10 – 15 | 25 – 30 |
где  - интервалы времени в часах;
- интервалы времени в часах;  - частоты интервалов, т.е. количество элементов, проработавших время в пределах соответствующего интервала. Требуется, используя критерий
- частоты интервалов, т.е. количество элементов, проработавших время в пределах соответствующего интервала. Требуется, используя критерий  при уровне значимости
при уровне значимости  проверить гипотезу о том, что время работы элементов распределено по показательному закону с плотностью вероятностей
проверить гипотезу о том, что время работы элементов распределено по показательному закону с плотностью вероятностей  .
.
2.4.6. В опытах наблюдалась неотрицательная непрерывная случайная величина 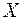 . Ее значения (упорядоченные по величине и округленные до двух знаков) для
. Ее значения (упорядоченные по величине и округленные до двух знаков) для  опытов оказались равными: (0,01; 0,01; 0,04; 0,17; 0,18; 0,22; 0,22; 0,25; 0,25; 0,29; 0,42; 0,46; 0,47; 0,56; 0,59; 0,67; 0,68; 0,70; 0,72; 0,76; 0,78; 0,83; 0,85; 0,87; 0,93; 1,00; 1,01; 1,01; 1,02; 1,03; 1,05; 1,32; 1,34; 1,37; 1,47; 1,50; 1,52; 1,54; 1,59; 1,71; 1,90; 2,10; 2,35; 2,46; 2,46; 2,50; 3,73; 4,07; 5, 55; 6,03).
опытов оказались равными: (0,01; 0,01; 0,04; 0,17; 0,18; 0,22; 0,22; 0,25; 0,25; 0,29; 0,42; 0,46; 0,47; 0,56; 0,59; 0,67; 0,68; 0,70; 0,72; 0,76; 0,78; 0,83; 0,85; 0,87; 0,93; 1,00; 1,01; 1,01; 1,02; 1,03; 1,05; 1,32; 1,34; 1,37; 1,47; 1,50; 1,52; 1,54; 1,59; 1,71; 1,90; 2,10; 2,35; 2,46; 2,46; 2,50; 3,73; 4,07; 5, 55; 6,03).
Проверить на основании этих данных гипотезу  , применяя критерий
, применяя критерий  и используя группировку с четырьмя равновероятными интервалами (уровень значимости принять равным
и используя группировку с четырьмя равновероятными интервалами (уровень значимости принять равным  ).
).
2.4.7. Наблюдались показания 500 наугад выбранных часов, выставленных в витринах часовщиков. Пусть  - номер промежутка от
- номер промежутка от  -го часа до
-го часа до  -го,
-го,  , а
, а  - число часов, показания которых принадлежали
- число часов, показания которых принадлежали  -му промежутку. Результаты наблюдений оказались следующими:
-му промежутку. Результаты наблюдений оказались следующими:

| ||||||||||||

|
Согласуются ли эти данные с гипотезой о том, что показания часов равномерно распределены на интервале  при уровне значимости
при уровне значимости  ?
?
2.4.8. В течение 10 часов регистрировали прибытие автомашин к бензоколонке и получили данные представленные в таблице.

| 
| 
| 
|
| 8 – 9 | 13 – 14 | ||
| 9 – 10 | 14 – 15 | ||
| 10 – 11 | 15 – 16 | ||
| 11 – 12 | 16 – 17 | ||
| 12 – 13 | 17 – 18 |
Требуется при уровне значимости  проверить гипотезу о том, что время прибытия автомашин распределено равномерно.
проверить гипотезу о том, что время прибытия автомашин распределено равномерно.
2.4.9. Четыре монеты подбрасывались одновременно 100 раз, причем каждый раз отмечалось число выпавших «гербов». Ниже приведены частоты  случаев, когда число выпавших «гербов» было равно
случаев, когда число выпавших «гербов» было равно 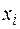 :
:
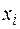
| |||||

|
Пользуясь критерием  , проверить согласие этих данных с гипотезой о биномиальном распределении числа выпавших «гербов», если вероятность выпадения «герба» при бросании каждой из монет равна 0,5. Уровень значимости принять равным
, проверить согласие этих данных с гипотезой о биномиальном распределении числа выпавших «гербов», если вероятность выпадения «герба» при бросании каждой из монет равна 0,5. Уровень значимости принять равным  .
.
2.4.10. Из 2020 семей, имеющих двух детей, в 527 семьях по два мальчика и в 476 – по две девочки (в остальных 1017 семьях дети разного пола). Можно ли с уровнем значимости  считать, что количество мальчиков в семье с двумя детьми – биномиальная случайная величина?
считать, что количество мальчиков в семье с двумя детьми – биномиальная случайная величина?
2.4.11. Выборка представляет собой целочисленный случайный вектор
(47, 46, 49, 53, 50). Можно ли с уровнем значимости  считать распределение наблюдавшейся случайной величины пуассоновским?
считать распределение наблюдавшейся случайной величины пуассоновским?
2.4.12. При  4040 бросаниях монеты было получено
4040 бросаниях монеты было получено  2048 выпадений «герба» и
2048 выпадений «герба» и  1992 выпадений «решки». Проверить, используя критерий
1992 выпадений «решки». Проверить, используя критерий  , совместимы ли эти данные с гипотезой о том, что монета была симметричной.
, совместимы ли эти данные с гипотезой о том, что монета была симметричной.
2.4.13. При  независимых испытаниях события
независимых испытаниях события  и
и  , образующие полную группу событий, осуществились 1905, 1015 и 1080 раз соответственно. Проверить, согласуются ли эти данные на уровне значимости
, образующие полную группу событий, осуществились 1905, 1015 и 1080 раз соответственно. Проверить, согласуются ли эти данные на уровне значимости  с гипотезой
с гипотезой  , где
, где  ,
,  .
.
2.4.14. Таблица «случайных чисел» содержит реализации 10 000 независимых и одинаково распределенных случайных величин, принимающих значения 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Корректно ли предположение о равновероятности этих значений, если в упомянутой таблице числа, не превосходящие 4, встречаются 4806 раз? При каком уровне значимости гипотеза равновероятности отвергается?