Алгоритм прямого счета и описание шаблонов
Описание строится для стержневой системы. Шаблон фермы является частным случаем.
Координаты узлов в глобальной системе координат XOY представлены в таблице 6. В шаблонах таблица заполняется вручную в соответствии с заданием.
Таблица 6
| Координаты | j | ||||
| узлов | |||||
| X, мм | 6000.0 | ||||
| Y,мм |
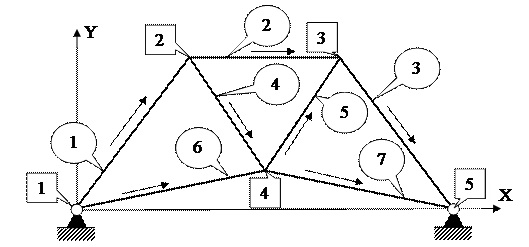
Рис.2. Конструкция стержневой системы, нумерация стержней, узлов, направление локальных координат сечений стержней.
Приняты обозначения: i – номера стержней, j – номера узлов, 
– координаты начала и конца стержня.
В примере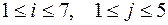 
. Координаты начала и конца стержней приведены в таблице 7. В шаблонах таблица 7 заполняется вручную. Направление перемещения от начала к концу произвольное.
Длины стержней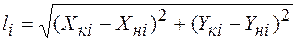 
вычисляется автоматически. Также автоматически вычисляются синус и косинус угла наклона 
стержня к оси OX с учетом выбранного направления
, 
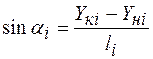. (4.1)
Таблица 7
| i | Xн | Yн | Xк | Yк |
Перемещения и повороты узлов (для сварной конструкции) в глобальной системе координат обозначаются 
. Некоторые значения равны нулю (для закрепленных узлов, в таблице 3 выделены жирно), остальные подлежат определению при решении задачи и объявляются изменяемыми параметрами при формирования «Поиска решения» и автоматически изменяются по завершении расчета. Рекомендуемое начальное заполнение таблицы в рассматриваемом примере приведено в таблице 8.
Таблица 8
| j | |||||
| Uj | |||||
| Vj | |||||
| φj | 0,1 | 0,1 | 0,1 | 0,1 | 0,1 |
В соответствии с заданием в соответствующие таблицы шаблона вносятся значения сил в узлах в проекции на глобальные оси 
и нагрузки на стержни в локальных системах координат 
и координата приложения силы 
. Также вносятся значения модулей упругости материалов стержней E, площадей сечения Fi и моментов инерции Ji.
После заполнения таблиц исходных данных в шаблоне автоматически вычисляются перемещения концов стержней в локальных системах координат 
. Для их вычисления предварительно формируются вспомогательные функции, зависящие от заданной конструкции стержневой системы:
, (4.2)
, (4.3)
. (4.4)
и, соответственно,
, (4.5)
, (4.6)
, (4.7)
, (4.8)
, (4.9)
, (4.10)
*В случае меньшего, чем предусмотрено в шаблоне, числа стержней и узлов координаты узлов задаются так, чтобы они не совпадали с началом и концом «лишних» стержней. Координаты начала и конца «лишних» стержней задаются такими, чтобы выполнялось условие 
.
Из аналитического решения задач растяжения и изгиба автоматически вычисляются внутренние силы на концах стержней в локальных системах координат:
, (4.11)
(4.12)
(4.13)
, (4.14)
, (4.15)
.(4.16)
Также автоматически вычисляются суммы сил и моментов в узлах в глобальной системе координат:
(4.17)
(4.18)
. (4.19)
Автоматически заполняется таблица 9. В ней предварительно выделяются цветом (в пособии жирным шрифтом) ячейки, которые будут целевыми при формировании целевой функции и ограничений в «Поиске решения».
Таблица 9
| Равновесие узлов (жирный шрифт-целевые ячейки) | |||||
| Rxj | 0.0000 | 0.0000 | 0.0000 | ||
| Ryj | 0.0000 | 0.0000 | 0.0000 | ||
| Lj | 5.96E-08 | 4.28E-08 | 0.00E+00 | 2.28E-08 | -6.52E-09 |
После выполнения «Поиска решения» определяются и, соответственно, остальные параметры. В том числе вычисляются модули максимальных нормальных напряжений в двадцати точках по длине и их максимальные значения для каждого стержня.
Шаблон фермы отличается от изложенного тем, что Q=0, M=0, q=0, L=0, φ не вычисляется.