Абсолютная и относительная погрешность
Абсолютной погрешностью приближенного числа называется модуль разности между этим числом и его точным значением. 
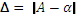. Отсюда следует, что 
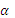заключено в пределах 
или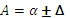 
.
Пример 1. На предприятии 1284 рабочих и служащих. При округлении этого числа до 1300 абсолютная погрешность составляет |1300 — 1284|=16. При округлении до 1280 абсолютная погрешность составляет |1280 — 1284| = 4.
Относительной погрешностью приближенного числа называется отношение абсолютной погрешности приближенного числа к модулю значения числа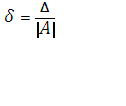 
.
Пример 2. В школе 197 учащихся. Округляем это число до 200. Абсолютная погрешность составляет |200 — 197| = 3. Относительная погрешность равна 3/|197| или 1,5 %.
В большинстве случаев невозможно узнать точное значение приближенного числа, а значит, и точную величину погрешности. Однако почти всегда можно установить, что погрешность (абсолютная или относительная) не превосходит некоторого числа.
Пример 3. Продавец взвешивает арбуз на чашечных весах. В наборе гирь наименьшая — 50 г. Взвешивание дало 3600 г. Это число – приближенное. Точный вес арбуза неизвестен. Но абсолютная погрешность не превышает 50 г. Относительная погрешность не превосходит 50/3600 ≈1,4%.
В примере 3 за предельную абсолютную погрешность можно взять 50 г, а за предельную относительную погрешность – 1,4 %.
Абсолютная погрешность обозначается греческой буквой Δ («дельта») или Da; относительная погрешность — греческой буквой δ («дельта малая»). Если приближенное число обозначить буквой А, то δ = Δ/|А|.
Значащей цифрой приближенного числа А называется всякая цифра в его десятичном представлении, отличная от нуля, и нуль, если он содержится между значащими цифрами или является представителем сохраненного десятичного разряда
Пример. А= 0,002080. Здесь только первые три нуля не являются значащими.
n первых значащих цифр приближенного числа А являются верными, если абсолютная погрешность этого числа не превышает половины разряда, выражаемого n – й значащей цифрой, считая слева направо. Цифры, не являющиеся верными, называются сомнительными.
Пример. Если в числе a= 0,03450 все цифры верные, то 
.
| Правила приближенных вычислений | ||
| понятие | определение | пример или примечание |
| Приближенные вычисления | Вычисления, производимые над числами, которые известны нам с определённой точностью, например, полученмо помнить о той точности, которую нужно или которую можно получить. Недопустимо вести вычисления с большой точностью, если данные задачи не допускают или не требуют этого. И наоборот. | |
| Погрешности | Разница между точным числом а и его приближенным значением А называется погрешностью данного приближенного числа. Если известно, что | а - А | < D, то величина D называется абсолютной погрешностью приближенной величины А. Отношение D /|А| = δ называется относительной погрешностью; последнюю часто выражают в процентах. | 3,14 является приближенным значением числа а, погрешность его равна 0,00159..., абсолютную погрешность можно считать равной 0,0016, а относительную погрешность δ равной 0.0016/3.14 = 0,00051 = 0,051%. |
| Значащие цифры | все цифры числа, начиная с 1-й слева, отличной от нуля, до последней, за правильность которой можно ручаться. | Приближенные числа следует записывать, сохраняя только верные знаки. Если, например, абсолютная погрешность числа 52438 равна 100, то это число должно быть записано, например, в виде 524 .102 или 0,524 .105. Оценить погрешность приближенного числа можно, указав, сколько верных значащих цифр оно содержит. Если число А = 47,542 получено в результате действий над приближенными числами и известно, что δ = 0,1%, то a имеет 3 верных знака, т.е. А = 47,5 |
| Округление | Если приближенное число содержит лишние (или неверные) знаки, то его следует округлить. | При округлении сохраняются только верные знаки; лишние знаки отбрасываются, причем если первая отбрасываемая цифра больше или равна 5, то последняя сохраняемая цифра увеличивается на единицу. |
| Действия над приближенными числами | Результат действий над приближёнными числами представляет собой также приближённое число. Число значащих цифр результата можно вычислить при помощи следующих правил: 1. При сложении и вычитании приближённых чисел в результате следует сохранять столько десятичных знаков, сколько их в приближённом данном с наименьшим числом десятичных знаков. 2. При умножении и делении в результате следует сохранять столько значащих цифр, сколько их имеет приближённое данное с наименьшим числом значащих цифр. |
Результат действий с приближенными числами есть тоже приближенное число. При этом неточными могут оказаться и те цифры, которые получены действиями над точными цифрами данных чисел.
Пример 5. Перемножаются приближенные числа 60,2 и 80,1. Известно, что все выписанные цифры верны, так что истинные величины могут отличаться от приближенных лишь сотыми, тысячными и т. д. долями. В произведении получаем 4822,02. Здесь могут быть неверными не только цифры сотых и десятых, но и цифры единиц. Пусть, например, сомножители получены округлением точных чисел 60,25 и 80,14. Тогда точное произведение будет 4828,435, так что цифра единиц в приближенном произведении (2) отличается от точной цифры (8) на 6 единиц.
Теория приближенных вычислений позволяет:
1) зная степень точности данных, оценить степень точности результатов еще до выполнения действий;
2) брать данные с надлежащей степенью точности, достаточной, чтобы обеспечить требуемую точность результата, но не слишком большой, чтобы избавить вычислителя от бесполезных расчетов;
3) рационализировать сам процесс вычисления, освободив его от тех выкладок, которые не окажут влияния на точные цифры результата.