Замечание.
1. Любую задачу максимизации можно свести к задаче минимизации, умножив целевую функцию на (-1), и наоборот.
2. При заполнении симплекс таблицы нужно обратить внимание на строку оценок: С0 берется со своим знаком, а коэффициенты Сj - с противоположным знаком из целевой функции.
Симплексный метод решения ЗЛП основан на переходе от одного опорного плана к другому, при котором значение целевой функции улучшается (возрастает или уменьшается), при условии, что данная задача имеет оптимальный план. Если известно опорное решение ЗЛП в канонической форме, то задачу решают симплекс-методом, который подразумевает направленный перебор опорных решений, при этом улучшается значение целевой функции: уменьшается (увеличивается) значение функции для задач минимизации (максимизации). Если на очередном шаге удается установить оптимальность опорного решения или неограниченность целевой функции, то следующий шаг не выполняется.
Алгоритм симплекс-метода
1. Заполняем симплекс-таблицу по данным задачи в каноническом виде (*).
2. Если выполнено условие оптимальности, то базисный план задачи оптимален и решение задачи получено.
3. Если выполняется условие неограниченности целевой функции, то задача не имеет решения.
4. Выбираем направляющий столбец S по наименьшему или наибольшему по модулю положительному (отрицательному) элементу строки оценок для задачи минимизации (максимизации).
5. Составляем отношения положительных элементов столбца свободных членов b к соответствующим положительным элементам направляющего столбца. Среди них выбираем наименьшее, т.е. если 
; то r – направляющая строка, и элемент ars - это генеральный или ключевой элемент на данном шаге.
6. Симплекс-таблицу приводят к новому базису, исключая из базиса переменную 
и вводя в базис переменную 
. Составляют новую симплекс-таблицу нового базиса, пересчитывая элементы по правилу жордановых преобразований:
1) Элементы направляющей строки умножаются на 1/ars.
2) Все остальные элементы пересчитываются по правилу прямоугольника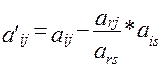 
7. Возвращаемся к пункту 2.
Пример. При условии предыдущего примера для решения применим симплекс-метод. Для задачи в основном виде
10x1+20x2≤100 10x1+20x2+x3=100
20x1+10x2≤100 получим 20x1+10x2+x4=100 - канонический
15x1+15x2≤90 15x1+15x2+x5=90 вид
ƒ(x1,x2)= 20x1+30x2 →max
Строим симплекс-таблицу:
| Базис | b | а1 | а2 | а3 | а4 | а5 |
| X3 | ||||||
| X4 | ||||||
| X5 | ||||||
| Оценки | -20 | -30 |
| Базис | b | а1 | а2 | а3 | а4 | а5 |
| X2 | 1/2 | 1/20 | ||||
| X4 | -0,5 | |||||
| X5 | 7,5 | -0,75 | ||||
| Оценки | -5 | 1,5 |
| Базис | b | а1 | а2 | а3 | а4 | а5 |
| X2 | 0,1 | -1/15 | ||||
| X4 | -2 | |||||
| X1 | -0,1 | 2/15 | ||||
| Оценки | 2/3 |
Т.к. все оценки последней симплекс-таблицы неотрицательны, то выполнено условие оптимальности, а, значит, получено оптимальное решение (см. столбец b последней симплекс-таблицы): αопт (2;4;0;20;0), т.е. x1=2; x2=4; x3=0; x4=20; x5=0. Экономический смысл переменных x3, x4, x5 – остатки сырья каждого вида: сырье 1 и 3-го вида израсходовано полностью, а сырье 2-го вида использовано на 80 единиц из 100. Значения x1=2; x2=4 определяют оптимальное время использования 1-го и 2-го технологических способов, что позволит получить наибольшее количество произведенной продукции ƒ(αопт)=160.