Автомат Мили

 

Конечный автомат Мили есть пятерка A= (X, Y, Z, f, g), где

 

· X – конечное множество входов,

· Y – конечное множество выходов,

· Z – конечное множество состояний,

· f: Z´X® Z – отображение (функция переходов),

· g: Z´X® Y – функция выходов, причем g – сюръекция.

 

Замечание:

1. Соответствие f: X® Y называется отображением, если каждое xÎX встречается ровно в одной паре (x, y) в графике соответствия.

2. Отображение называется сюръективным, если f(x)= y.

Требование сюръективности для отображения g не является существенным ограничением. Действительно, в Y не имеет смысла включать элементы, которые заведомо не могут появиться на выходе. Однако часто множество выходов определяют «с запасом», т.е. больше, чем это необходимо в действительности.

Автоматы Мили могут быть представлены в виде графов и при помощи переходно-выходной матрицы.

Пусть А= (X, Y, Z, f, g), где Z= {z₁, z₂,…, z_n}.

Тогда переходно-выходной матрицей для А называется nxn матрица M= ||m_ik||, где .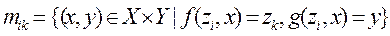

 

Замечание: в дальнейшем будем считать, что ни одно из множеств X, Y, Z не пусто.

Вопросы и упражнения

1. Существует ли отображение, не являющееся сюрьекцией ? Приведите пример.

2. Задайте Автоматом Мили процесс решения квадратного уравнения.