Аппроксимации характеристики

 

7.5.1. Гармонический сигнал на входе

 

Предположим, что рабочий участок характеристики нелинейного элемента описывается полиномом

.

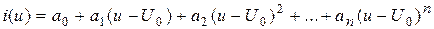На вход поступает гармонический сигнал 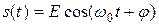. Тогда с учетом напряжения рабочей точки входное воздействие на элемент равно

.

Подставив данное выражение в формулу степенного полинома, получаем

.

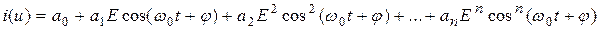Воспользуемся известными формулами для степеней тригонометрических функций

; ; ; .

В результате получается общее выражение для тока в нелинейной цепи

=

.

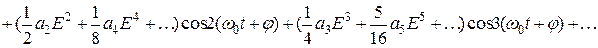Анализ данного выражения позволяет сделать следующие выводы:

1. Спектр тока содержит гармонические составляющие с частотами 0, , , , 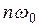и начальными фазами , , 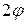, , 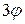т.е с частотами и начальными фазами, кратными частоте и начальной фазе воздействия.

2. Номер гармоники в спектре тока не может быть выше степени аппроксимируемого полинома.

3. Амплитуды гармонических составляющих спектра зависят от амплитуды входного сигнала и коэффициентов степенного полинома. Постоянная составляющая (нулевая гармоника) и амплитуды четных гармоник определяются коэффициентами полинома с четными номерами, а амплитуды нечетных гармоник – коэффициентами полинома с нечетными номерами.

Полученное выражение сохранит свою структуру при поступлении на вход нелинейного элемента амплитудно-модулированного сигнала или сигнала с угловой модуляцией. В формуле будут фигурировать не постоянные значения и , а функци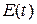и и 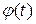. Общая структура спектра изменится. В то же время начальная фаза первой гармоники сохраняет закон модуляции фазы входного сигнал, а если характеристика нелинейного элемента может быть с достаточной точностью аппроксимирована полиномом второй степени, то первая гармоника спектра сохранит также и форму входного амплитудно-модулированного сигнала.

Пользуясь полученными результатами и структурной схемой нелинейного устройства, можно предложить общую идею построения некоторых радиотехнических устройств. Так, если фильтр нелинейного устройства с квадратичной характеристикой настроить на частоту первой гармоники тока (на частоту входного сигнала), то получится схема усилителя мощности. Если фильтр нелинейного устройства настроить на частоту второй гармоники тока, то получится схема удвоителя частоты сигнала. Если в качестве фильтра использовать фильтр низких частот с АЧХ, обеспечивающей подавление всех гармоник, кроме нулевой, то получится схема квадратичного детектора.

 

7.5.2. Бигармонический сигнал на входе

 

Свойство нелинейной цепи обогащать спектр сигнала хорошо проявляется, если сигнал представляет собой сумму некоторого числа гармонических колебаний с различными частотами.

Предположим, что рабочий участок характеристики нелинейного элемента описывается полиномом второй степени

.

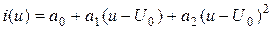На вход поступает бигармонический сигнал, формула которого совместно с напряжением рабочей точки имеет вид

.

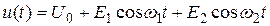Подставив данное выражение в формулу степенного полинома, получаем

.

Выполним элементарные преобразования:

.

.

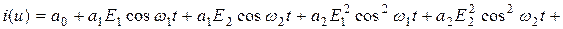
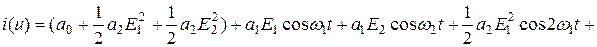
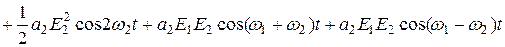Из полученного выражения видно, что в спектре тока нелинейного элемента кроме постоянной составляющей (слагаемое в скобках) и гармоник с частотами, кратными частотам входного воздействия, имеются гармоники с комбинационными частотами и .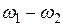

Таким образом, с помощью нелинейного элемента с такой характеристикой можно построить схему преобразователя частоты. Для этого достаточно использовать в составе нелинейного устройства высокодобротный полосовой фильтр, настроенный на частоту (или на частоту 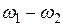). На вход устройства подается гармонический сигнал, частота которого должна быть преобразована, и вспомогательный сигнал с частотой 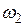(сигнал гетеродина).