Задача. Оценка параметров нелинейного уравнения.
Данные результатов наблюдений представлены в таблице.
| x | -2 | -1 | |||
| y | 7,5 | 4,0 | 3,0 | 5,2 | 10,0 |
Требуется:
- Определить МНК параметры
зависимости вида 
- Вычислить индекс корреляции и сделать вывод о тесноте связи между заданными величинами x и y.
Решение.
1. Для нахождения параметров данной модели необходимо решить систему уравнений
Необходимые вычисления приведем в таблице.
| № | x | y | 
| 
| 
| 
| 
|
| -2 | 7,5 | -8 | -15 | ||||
| -1 | 4,0 | -1 | -4 | ||||
| 3,0 | |||||||
| 5,2 | 5,2 | 5,2 | |||||
| 10,0 | |||||||
| ∑ | 29,7 | 6,2 | 79,2 |
На основании полученных результатов система примет вид
Решая эту систему методом Крамера, получим 
. Таким образом, уравнение нелинейной регрессии на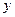 
примет вид 
.
2. Для определения индекса корреляции по формуле 
найдем теоретические значения результата 
, подставляя в полученное выражение фактические значения 
. Результаты вычислений представим в таблице.
| № | 
|
| 
| 
| 
| 
| 
|
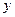
| -2 | 7,5 | 7,51 | -0,01 | 0,0001 | 1,56 | 2,4336 | |
| -1 | 4,0 | 3,9 | 0,1 | 0,01 | -1,94 | 3,7636 | |
| 3,0 | 3,11 | -0,11 | 0,0121 | -2,94 | 8,6436 | ||
| 5,2 | 5,14 | 0,06 | 0,0036 | -0,74 | 0,5476 | ||
| 10,0 | 9,99 | 0,01 | 0,0001 | 4,06 | 16,4836 | ||
| ∑ | 29,7 | - | - | 0,0259 | - | 31,872 |
Вычислим индекс корреляции 
Индекс корреляции близок к единице, поэтому можно сделать вывод о довольно тесной связи между заданными величинами.