Исходные данные для построения уравнений регрессии
| №/№ | y | x1 | x2 | №/№ | y | x1 | x2 |
| 48,01 | 0,91 | 46,08 | 36,26 | 0,90 | 40,06 | ||
| 38,18 | 0,76 | 45,18 | 32,07 | 0,52 | 57,91 | ||
| 38,7 | 0,82 | 41,76 | 32,83 | 0,66 | 43,86 | ||
| 46,72 | 0,88 | 50,94 | 35,16 | 0,58 | 58,62 | ||
| 41,58 | 0,88 | 43,54 | 44,56 | 0,99 | 44,39 | ||
| 36,89 | 0,89 | 38,8 | 59,16 | 1,63 | 35,77 | ||
| 34,54 | 0,87 | 39,22 | 67,99 | 1,95 | 35,96 | ||
| 42,86 | 0,94 | 42,74 | 53,73 | 1,27 | 40,99 | ||
| 38,97 | 0,91 | 41,2 | 52,39 | 1,55 | 33,05 | ||
| 43,22 | 1,07 | 39,35 | 36,1 | 1,15 | 30,68 | ||
| 28,19 | 0,69 | 34,38 | 32,67 | 0,94 | 34,26 | ||
| 38,65 | 0,74 | 48,98 | Σ | 959,43 | 22,5 | 967,72 |
В табл. 2.1 используются следующие обозначения:
y – сбор хлеба (зерна) на душу населения (пуд);
x1 – размер посевных площадей на душу населения (десятин);
x2 – урожайность зерна (пуд с десятины).
Попытаемся представить интересующую нас зависимость с помощью прямой линии.
Разумеется, такая линия может дать только приближенное представление о форме реальной статистической связи. Постараемся сделать это приближение наилучшим.
Оно будет тем лучше, чем меньше исходные данные будут отличаться от соответствующих точек, лежащих на линии. Степень близости может быть выражена величиной суммы квадратов отклонений реальных значений от значений, расположенных на прямой линии. Использование именно квадратов отклонений (не просто отклонений) позволяет суммировать отклонения различных знаков без их взаимного погашения и дополнительно обеспечивает сравнительно большее внимание, уделяемое большим отклонениям. Именно этот критерий (минимизация суммы квадратов отклонений) положен в основу метода наименьших квадратов.
В вычислительном аспекте метод наименьших квадратов сводится к составлению и решению системы так называемыхнормальных уравнений(о которой мы уже говорили ранее). Исходным этапом для этого является подбор вида функции, отображающей статистическую связь.
Тип функции в каждом конкретном случае можно подобрать путем прикидки на графике исходных данных подходящей, т. е. достаточно хорошо приближающей эти данные, линии. В нашем случае связь между сбором хлеба на душу населения и величиной посевных площадей на душу может быть изображена с помощью прямой линии и записана в виде:
y = a0 + a1x (2.12)
где у- величина сбора хлеба на душу (результативный признак или зависимая переменная); x—величина посева на душу (факторный признак или независимая переменная); ao и a1 — параметры уравнения, которые могут быть найдены методом наименьших квадратов.
Для нахождения искомых параметров нужно составить систему уравнений, которая в данном случае будет иметь вид
 |
na0 + a1Σx = Σy;
(2.13)
a0Σx + a1Σx2 = Σxy.
Система (2.14) может быть решена известным методом определителей. Но, как уже известно из курса теории статистики, можно вычислить искомые параметры и непосредственно с помощью использования формул:

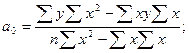
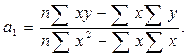 (2.14)
(2.14)
где Σy – сумма значений результативного признака; Σx – сумма значений факторного признака; Σx2 – сумма квадратов значений факторного признака; Σxy – сумма произведений значений результативного и факторного признаков; n– число значений признака y, или, что то же самое, число значений признака x.
Пример. Найдем уравнение линейной регрессии между величиной сбора хлеба на душу населения (у) и размером посевных площадей на душу населения (х1) по данным табл. 2.1. Построим вспомогательную таблицу для расчета параметров парной линейной регрессии (табл.2.2).
Для того, чтобы сделать таблицу более компактной, исходные данные сгруппированы в два столбца, и точно также сгруппированы вспомогательные расчеты. Итоговые суммы, рассчитанные в последних четырех графах (столбцах) таблицы 2.2., представляют собой итоги по всей последовательности из 23х исходных значений.
Таблица 2.2.
Вспомогательная таблица для расчета параметров уравнения
y = a0 + a1x
| y | x1 | x12 | x1y | y | x1 | x12 | x1y | |
| 48,01 | 0,91 | 0,83 | 43,69 | 36,26 | 0,90 | 0,81 | 32,63 | |
| 38,18 | 0,76 | 0,58 | 29,02 | 32,07 | 0,52 | 0,27 | 16,68 | |
| 38,70 | 0,82 | 0,67 | 31,73 | 32,83 | 0,66 | 0,44 | 21,67 | |
| 46,72 | 0,88 | 0,77 | 41,11 | 35,16 | 0,58 | 0,34 | 20,39 | |
| 41,58 | 0,88 | 0,77 | 36,59 | 44,56 | 0,99 | 0,98 | 44,11 | |
| 36,89 | 0,89 | 0,79 | 32,83 | 59,16 | 1,63 | 2,66 | 96,43 | |
| 34,54 | 0,87 | 0,76 | 30,05 | 67,99 | 1,95 | 3,80 | 132,58 | |
| 42,86 | 0,94 | 0,88 | 40,29 | 53,73 | 1,27 | 1,61 | 68,24 | |
| 38,97 | 0,91 | 0,83 | 35,46 | 52,39 | 1,55 | 2,40 | 81,20 | |
| 43,22 | 1,07 | 1,14 | 46,25 | 36,10 | 1,15 | 1,32 | 41,52 | |
| 28,19 | 0,69 | 0,48 | 19,45 | 32,67 | 0,94 | 0,88 | 30,71 | |
| 38,65 | 0,74 | 0,55 | 28,60 | 959,43 | 22,50 | 24,57 | 1001,24 |
Подставив суммы, рассчитанные в последней (итоговой) строке четырех последних граф таблицы 2.2, в формулы (2.14) и проделав необходимые вычисления, получим:
a0 = 17, 8
a1 = 24, 5
Таким образом, уравнение парной линейной регрессии выглядит следующим образом:
у = 17,8+ 24,5x (2.15)
Построив любое уравнение регрессии, всегда необходимо убедиться, что именно данное уравнение наиболее точно описывает реально существующую статистическую зависимость между показателями x и y. Для этого используются специальные методы, которые мы рассмотрим на последующих лекциях.
Сейчас мы остановимся на вопросе о том, какой содержательный смысл имеют коэффициенты парной регрессии, какие выводы можно сделать на основе их расчета, и как рассчитать их точность.
4й учебный вопрос. Интерпретация и ошибки коэффициентов парной регрессии.
Очень важно иметь в виду, что уравнение регрессии не только определяет форму анализируемой связи, но и показывает, в какой степени изменение одного признака сопровождается изменением другого признака.
Коэффициент при х, называемыйкоэффициентом регрессии, показывает, на какую величину в среднем изменяется результативный признак у при изменении факторного признака х на единицу.
В нашем примере коэффициент регрессии получился равным 24,5. Это означает, что с увеличением посева, приходящегося на душу, на одну десятину, сбор хлеба на душу населения в среднем увеличивается на 24,5 пуда.
Средняя и предельная ошибки коэффициента регрессии.Поскольку уравнения регрессии рассчитываются, как правило, для выборочных данных, обязательно встают вопросы точности и надежности полученных результатов. Вычисленный коэффициент регрессии, будучи выборочным, с некоторой точностью оценивает соответствующий коэффициент регрессии генеральной совокупности. Представление об этой точности дает средняя ошибка коэффициента регрессии (μa1), которая рассчитывается по формуле:
μa1 = σy(x) / (σx√n) (2.16)
где
σy(x) = √Σ(уi - ŷi)2/(n-m-1) (2.17)
уi, — i-e значение результативного признака; ŷi — i-e выравненное значение, полученное на основе уравнения (2.15); xi—i-e значение факторного признака; σx—среднее квадратическое отклонение х; n — число значений х или, что то же самое, значений у; m—число факторных признаков (независимых переменных).
В формуле (2.17), в частности, формализовано очевидное положение: чем больше фактические значения отклоняются от выравненных, тем большую ошибку следует ожидать; чем меньше число наблюдений, на основе которых строится уравнение, тем больше будет ошибка.
Средняя ошибка коэффициента регрессии является основой для расчета предельной ошибки. Предельная ошибка показывает, в каких пределах находится истинное значение коэффициента регрессии при заданной надежности результатов. Предельная ошибка коэффициента регрессии вычисляется аналогично предельной ошибке средней величины выборки, т. е. как t μa1 где t—величина, числовое значение которой определяется по таблице распределения Стьюдента.
Найдем среднюю и предельную ошибки коэффициента регрессии, полученного в рассмотренном примере. Для расчета μa1 прежде всего подсчитаем выравненные по регрессии (или расчетные) значения ŷi . Для этого в уравнение регрессии, полученное в примере, подставим конкретные значения xi:
ŷi = 17,8 +24,5*0,91 = 41,22 и т. д.
Затем вычислим отклонения фактических значений уi, от выравненных и их квадраты.
Далее, подсчитав средний по губерниям посев на душу населения (  =0,98), найдем отклонения фактических значений xi от этой средней, квадраты отклонений, дисперсию и среднее квадратическое отклонение
=0,98), найдем отклонения фактических значений xi от этой средней, квадраты отклонений, дисперсию и среднее квадратическое отклонение  , получим все необходимые составляющие формул (2.16) и (2.17):
, получим все необходимые составляющие формул (2.16) и (2.17):

Таким образом, средняя ошибка коэффициента регрессии a1 равна 2,89, что составляет 12% от вычисленного значения коэффициента a1.
Заключение.Таким образом, на данной лекции мы рассмотрели математические основы и теоретические предпосылки метода наименьших квадратов (МНК) и пример его использования для построения уравнения парной линейной регрессии. Рассмотрели также понятия «несмещенные», «эффективные» и «состоятельные» оценки параметров регрессии и способы проверки предпосылок МНК. Затем, на конкретном примере было рассмотрено понятие средней и предельной ошибки параметра уравнения регрессии.