Методы расчета коммутационных систем с явными потерями вызовов
Исходными данными для расчета количества соединительных линий и приемников и датчиков сигналов управления являются величины расчетных нагрузок и вероятности потерь по вызовам (табл.).
Таблица
Показатели качества обслуживания
| Наименование показателя качества обслуживания | Допустимое значение показателя качества |
| Вероятность потерь при связях: по исходящим соединительным линиям к ЖАТС, ГАТС, УАТС, УАК к столу заказов РМТС и справочной службе по входящим соединительным линиям от ЖАТС, ГАТС, УАТС, УАК по входящим соединительным линиям от РМТС | 0,01 0,001 0,01 0,001 |
Выбор расчетной формулы зависит от вида пучка линий, который в свою очередь определяется структурой коммутационного поля АТС. Различают полно- и неполнодоступные, блокируемые и неблокируемые пучки. Если источники нагрузки, обслуживаемые пучком из V линий, разделены на группы, причем источникам каждой группы доступны D из V линий ( 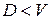 ), то такой пучок называется неполнодоступным. В полнодоступном пучке каждому источнику нагрузки доступны все V линий, т. е.
), то такой пучок называется неполнодоступным. В полнодоступном пучке каждому источнику нагрузки доступны все V линий, т. е. 
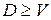 . Доступность D определяется конструкцией искателей (соединителей) телефонной станции. Для АТС декадно-шаговой системы доступность D = 10, для координатных АТСК 100/2000 – D = 20 или 10, для координатных АТСКУ – D = 20 или 40.
. Доступность D определяется конструкцией искателей (соединителей) телефонной станции. Для АТС декадно-шаговой системы доступность D = 10, для координатных АТСК 100/2000 – D = 20 или 10, для координатных АТСКУ – D = 20 или 40.
Полно- и неполнодоступные пучки могут быть блокируемыми или неблокируемыми. Блокируемые пучки образуются при включении линий в многозвенное коммутационное поле. В них возникают потери по причине занятости промежуточных линий между звеньями поля при наличии свободных линий пучка. В неблокируемых пучках потери вызовов возникают только из-за занятости линий самого пучка.
Полнодоступные неблокируемые пучки образуются в АТС декадно-шаговой системы (при 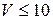 ), а также в электронных (цифровых) АТС и ручных коммутаторах. Расчет числа линий полнодоступных неблокируемых пучков производится по первой формуле Эрланга:
), а также в электронных (цифровых) АТС и ручных коммутаторах. Расчет числа линий полнодоступных неблокируемых пучков производится по первой формуле Эрланга:
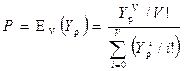 , (6.1)
, (6.1)
где 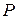 – потери по вызовам;
– потери по вызовам;
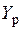 – расчетное значение поступающей нагрузки;
– расчетное значение поступающей нагрузки;
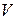 – число линий пучка;
– число линий пучка;
 – краткая условная форма записи первой формулы Эрланга для пучка из
– краткая условная форма записи первой формулы Эрланга для пучка из 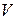 линий и нагрузки
линий и нагрузки 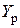 .
.
График P = Ev(Yp), построенный по данным, рассчитанным по формуле (6.1), приведен на рис. 6.1. Первая формула Эрланга, кроме случая расчета полнодоступного неблокируемого пучка, применяется в качестве вспомогательной при расчетах более сложных пучков.
Неполнодоступные неблокируемые пучки образуются преимущественно в декадно-шаговых АТС. Для их расчета можно воспользоваться методом О'Делла. Число линий в пучке в этом случае
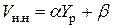 , (6.2)
, (6.2)
где 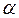 и
и 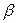 – коэффициенты, зависящие от вероятности потерь
– коэффициенты, зависящие от вероятности потерь 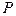 и доступности
и доступности 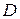 .
.
Значения коэффициентов 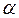 и
и 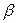 для наиболее часто встречающихся значений
для наиболее часто встречающихся значений 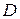 приведены в табл..
приведены в табл..
Таблица
Значения коэффициентов 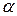 и
и 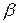
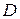
| 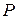 = 0,001 = 0,001
| 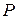 = 0,01 = 0,01
| ||
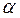
| 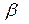
| 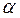
| 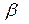
| |
| 1,99 | 3,88 | 1,58 | 2,9 | |
| 1,41 | 6,9 | 1,25 | 4,9 | |
| 1,19 | 10,9 | 1,12 | 7,2 |
В тех случаях, когда доступность принимает другие значения (в том числе и дробные), следует воспользоваться формулой Пальма-Якобеуса:
 . (6.3)
. (6.3)
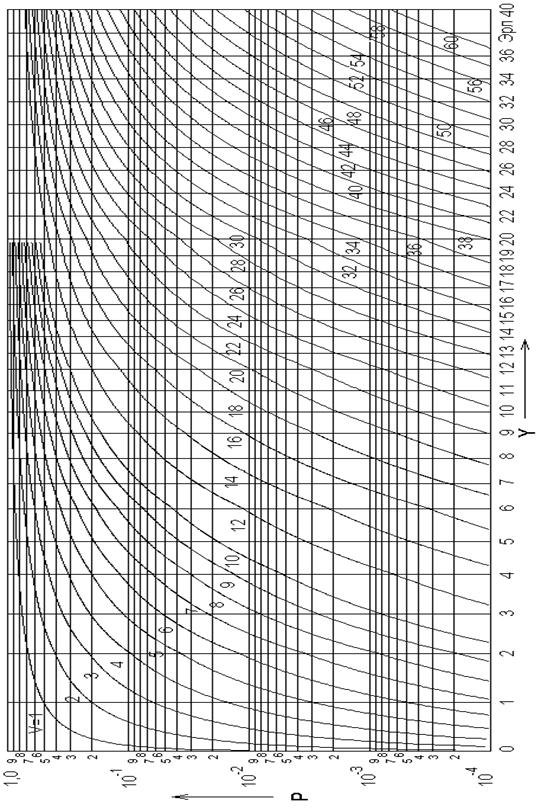
| Рис. 6.1. График для определения числа линий по первой формуле Эрланга |
Полнодоступные блокируемые пучки, образуемые двухзвенными ступенями искания, встречающимися, например, в координатных АТС, можно рассчитать с помощью формулы Якобеуса:
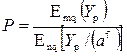
 , (6.4)
, (6.4)
где 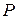 – заданная норма потерь;
– заданная норма потерь;
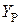 – расчетное значение нагрузки, поступающей на пучок соединительных линий;
– расчетное значение нагрузки, поступающей на пучок соединительных линий;
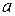 – расчетная нагрузка, приходящаяся на один вход блока ГИ;
– расчетная нагрузка, приходящаяся на один вход блока ГИ;
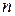 ,
, 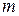 ,
, 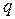 ,
, 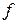 – параметры блока ГИ.
– параметры блока ГИ.
Необходимое для расчета значение числа линий пучка выражается через параметры блока: 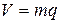 .
.
Для блоков группового искания АТСК 100/2000, имеющих 30 входов, 40 промежуточных линий и 200 выходов, структурные параметры будут следующие: число коммутаторов звена B m = 20, число коммутаторов звена А n = 15, связность f = 1, доступность в направлении D = 20. Неизвестно количество линий нужного направления 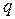 из каждого коммутатора звена B, а следовательно, и общее количество линий от всех коммутаторов звена B – искомое
из каждого коммутатора звена B, а следовательно, и общее количество линий от всех коммутаторов звена B – искомое 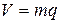 .
.
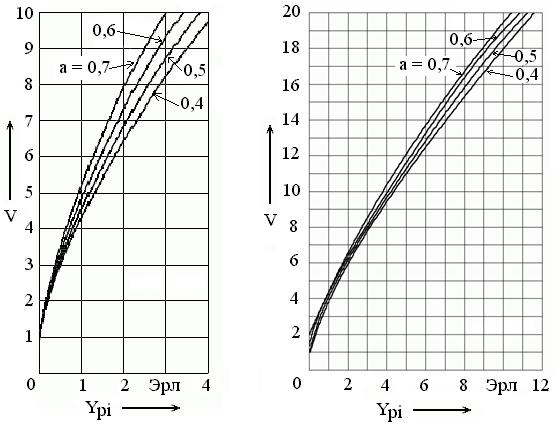
Для упрощения расчетов по формуле (6.4) составлены графики 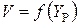 для ряда значений
для ряда значений 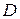 и
и 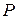 , которые приведены на рис. 6.3.
, которые приведены на рис. 6.3.
Для расчета числа линий 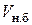 неполнодоступного блокируемого пучка с доступностью
неполнодоступного блокируемого пучка с доступностью 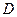 , включаемого в двухзвенные ступени искания, служит формула ЦНИИС-ЛФ:
, включаемого в двухзвенные ступени искания, служит формула ЦНИИС-ЛФ:
 , (6.5)
, (6.5)
где 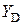 – пропускная способность полнодоступного неблокируемого пучка при доступности
– пропускная способность полнодоступного неблокируемого пучка при доступности 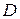 . Определяется по первой формуле Эрланга (6.1) при
. Определяется по первой формуле Эрланга (6.1) при 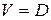 и заданных потерях
и заданных потерях 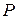 ;
;
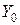 – нагрузка, поступающая к полнодоступному блокируемому пучку при
– нагрузка, поступающая к полнодоступному блокируемому пучку при 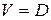 , определяется по формуле Якобеуса (6.4);
, определяется по формуле Якобеуса (6.4);
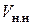 – число линий неблокируемого неполнодоступного пучка с доступностью
– число линий неблокируемого неполнодоступного пучка с доступностью 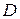 , который обусловливает потери
, который обусловливает потери 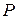 при заданной расчетной нагрузке
при заданной расчетной нагрузке 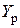 . Значение
. Значение 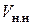 определяется по формуле О'Делла (6.2).
определяется по формуле О'Делла (6.2).
Полнодоступные блокируемые пучки, образованные в квазиэлектронных АТС с числом звеньев коммутации три и более, целесообразно рассчитывать с помощью метода эффективной доступности, сущность которого состоит в замене рассматриваемого полнодоступного блокируемого пучка неполнодоступным неблокируемым с искомым числом линий 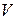 и эффективной доступностью
и эффективной доступностью 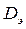 . Эта замена позволяет выполнять вычисления по формуле Пальма-Якобеуса (6.3).
. Эта замена позволяет выполнять вычисления по формуле Пальма-Якобеуса (6.3).
а б
Рис. 6.3. Определение числа линий полнодоступного блокируемого пучка:
а – для 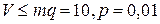 ; б – для
; б – для 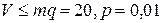
Таким образом, задача состоит в определении доступности 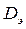 , которая рассчитывается по формуле:
, которая рассчитывается по формуле:
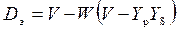 , (6.6)
, (6.6)
где 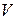 – искомое число линий, определяемое подбором;
– искомое число линий, определяемое подбором;
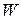 – вероятность занятости всех соединительных путей от входа в первое звено до линии рассматриваемого пучка, включенной в выход последнего звена (вероятность блокировки линии);
– вероятность занятости всех соединительных путей от входа в первое звено до линии рассматриваемого пучка, включенной в выход последнего звена (вероятность блокировки линии);
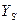 – расчетная нагрузка, приходящаяся на один выход последнего звена.
– расчетная нагрузка, приходящаяся на один выход последнего звена.
Входящие в формулу (6.6) переменные могут быть определены на основании расчета нагрузок и анализа коммутационной системы АТСКЭ "Квант". Можно принять: 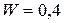 и
и 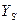 = 0,4 Эрл.
= 0,4 Эрл.
Расчеты числа линий блокируемых пучков АТСКЭ "Квант" по методу эффективной доступности выполняются подбором числа линий в следующей последовательности:
1) выбирается начальное значение искомого числа линий V, рекомендуется это значение определить по первой формуле Эрланга (6.1);
2) определяется эффективная доступность 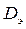 по формуле (6.6);
по формуле (6.6);
3) при  (округление – до целого числа в меньшую сторону), находится вероятность потерь
(округление – до целого числа в меньшую сторону), находится вероятность потерь 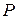 по формуле Пальма-Якобеуса (6.3).
по формуле Пальма-Якобеуса (6.3).
Если вероятность 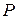 окажется равной или меньше заданного значения вероятности потерь, то выбранное значение
окажется равной или меньше заданного значения вероятности потерь, то выбранное значение 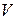 будет правильным. В противном случае значение
будет правильным. В противном случае значение 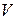 увеличивается на единицу и повторяются расчеты по формулам (6.6) и (6.3) до тех пор, пока вероятность
увеличивается на единицу и повторяются расчеты по формулам (6.6) и (6.3) до тех пор, пока вероятность 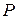 не окажется меньшей или равной заданному значению нормы потерь.
не окажется меньшей или равной заданному значению нормы потерь.