Метод наименьших квадратов

Рассмотрим задачу «наилучшей» аппроксимации набора наблюдений (x1 , y1), … (xn , yn) линейной функцией.

Общий смысл оценивания по методу наименьших квадратов заключается в минимизации суммы квадратов отклонений наблюдаемых значений зависимой переменной от значений, предсказанных моделью. Более точно, оценки наименьших квадратов (МНК-оценки) получаются минимизацией функции:

min.

(13)

Для краткости опустим индексы суммирования у знака суммы, при этом отметим, что суммирование проводится по всем наблюдаемым значениям от 1 до n.

Заметим, что S есть мера ошибки, возникающей при аппроксимации выборки прямой. Оценки a и b минимизируют ошибку .

Запишем необходимые условия экстремума:

.

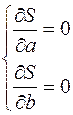(14)

Взяв частные производные, получим:

.

(15)

Раскроем скобки:

.

(16)

Отметим, что

.

(17)

 

Тогда можно записать:

.

(18)

Выразив из первого уравнения a и подставив полученное выражение во второе уравнение, получим:

.

(19)

Преобразуя, получим:

.

(20)

Из последнего уравнения можно получит зависимости для определения оценок параметров модели регрессии:

.

(21)

Варианты выражения для коэффициента регрессии b через отклонения, ковариацию и дисперсию.

Разност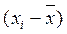и и называются отклонениями от средних по выборке значений. Вспомним выражения для выборочной дисперсии и ковариации:

.

(22)

 

Преобразуем сумму квадратов отклонений:

.

(23)

Преобразуем сумму произведений отклонений:

.

(24)

Теперь можно записать выражение для b через отклонения:

.

(25)

Умножив последнее равенство на 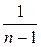, получим выражения для b через выборочную ковариацию и дисперсию:

.

(26)