Формирование у младших школьников представлений об окружности и круге
Одной из основных задач изучения элементов геометрии в начальных классах является расширение и уточнение представлений учащихся о геометрических фигурах, развитие пространственного мышления и формирование практических навыков.
Ученики проявляют большой интерес к геометрическим фигурам и их свойствам, поэтому перечень геометрических понятий, с которыми знакомятся младшие школьники в программе по математике авторского коллектива под руководством М.И. Моро, расширился. Например, в III классе ученики знакомятся с понятиями круг и окружность. Знакомство с этими фигурами осуществляется на уровне представлений.
Ученики должны научиться узнавать круг и окружность; знать, что окружность — это линия, являющаяся границей круга; уметь строить с помощью циркуля окружность; знать, что такое радиус окружности (круга). Для решения этих учебных задач используются различные практические упражнения. При их подборе, выборе методов и приемов работы с ними необходимо учитывать те подходы к определению окружности и круга, которые имеют место в школьном курсе геометрии.
В школьной трактовке окружность определяется разными способами:
а) окружностью называется замкнутая кривая линия, все точки которой равноудалены от определенной точки, находящейся внутри замкнутой линии;
б) окружностью называется фигура, которая состоит из всех точек плоскости, равноудаленных от данной точки. Эта точка называется центром окружности.
При знакомстве с окружностью в III классе лучше опираться на первое определение, используя метод практических работ в сочетании с беседой.
Покажем, как можно познакомить третьеклассников с понятием «окружность».
На доске нарисованы различные фигуры.
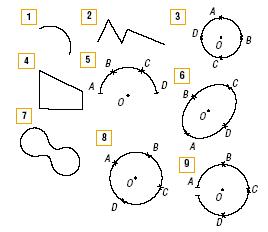
— Какие из нарисованных на доске фигур можно назвать линиями? (Все.) Уточните, какие из нарисованных на доске линий являются ломаными, а какие — кривыми? (Линии 2 и 4 — ломаные; линии 1, 3, 5, 6, 7, 8 и 9 — это кривые.) Распределите кривые линии на две группы: замкнутые и незамкнутые. Какие фигуры будут в первой группе и какие во второй? (Замкнутые кривые — это линии 3, 6, 7 и 8; незамкнутые кривые линии — 5 и 9.) В фигурах 3, 6 и 8, которые являются замкнутыми кривыми линиями, расставлены точки. Можно ли утверждать, что расстояния от точки О до точек А, В, С и D в каждой фигуре одинаковые? (В фигуре 6 расстояния от точки О до точек А, В, С, D неодинаковые, а в фигурах 3 и 8 — одинаковые.)
К доске приглашаются три ученика. Они должны убедить класс в том, что расстояние от точки О до точек А, В, С и D в фигурах 3 и 8 одинаковое, а в фигуре 6 — разное. Ученики могут воспользоваться линейкой или циркулем.
Остальные ученики класса сравнивают фигуры 6 и 8. (Сходство: это замкнутые кривые линии; в центре каждой фигуры отмечена точка О; на фигурах отмечены точки А, В, С и D. Отличия: расстояния от точки О до точек А, В, С, D в фигуре 6 — разные, в фигуре 8 — одинаковые.)
— Как вы думаете, почему фигура 8 является окружностью, а фигура 6 не является окружностью? (В фигуре 8 расстояния от точки О до точек А, В, С и D одинаковые, а в фигуре 6 — разные.) Назовите существенные признаки окружности. (Кривая замкнутая линия; расстояния от точки О, которая расположена в центре, до точек на окружности одинаковые.) Можно ли назвать окружностями фигуры 9, 5 и 7? (Нет. Фигуры 9 и 5 не являются замкнутыми кривыми, а фигура 7 не имеет центра.) Чем отличаются окружности 3 и 8? (Расстоянием от точки О до точек на окружности.) Если мы отметим любую точку на окружности 8 и измерим расстояние от точки О (центра окружности) до данной точки, то будет ли оно таким же, как и расстояние от точки О до точек А, В, С, D? (Да.) Расстояние от центра окружности О до любой точки на окружности называется радиусом и обозначается латинской буквой R. Используя циркуль, постройте в тетрадях две окружности с одинаковым радиусом, равным 2 см.
Учитель предлагает учащимся закрасить ту часть тетради, которая ограничена первой окружностью. В это время учитель вывешивает на доске большой лист бумаги с таким же рисунком, как у учеников.

— Как вы думаете, закрашенной фигуре принадлежат только точки окружности или ей принадлежат и другие точки? (Так как первая фигура закрашена, то ей принадлежат все точки окружности, а также точки, которые находятся внутри окружности.)
Первая фигура называется круг. Послушайте следующее стихотворение и постарайтесь разрешить возникающий спор между кругом и окружностью.
Встретились окружность с кругом.
Спорить стали вот о чем.
Кто главнее всех в округе?
Кто сначала, кто потом?
Круг сказал, что он главнее:
«Я большой и, посмотри,
Весь заполнен в середине,
Есть по краю и внутри».
Тут воскликнула окружность:
«Жить не сможешь без меня!
Я ведь линия сплошная,
И граница я твоя!»
Долго спорили фигуры,
Кто из них кого главней,
И соседей опросили,
И знакомых, и друзей,
Но закончить этот спор
Не смогли и до сих пор.
В чью же пользу и без ссор
Разрешится этот спор?
Ученики высказывают свои мнения о том, кого они считают главнее.
— Окружность и круг являются древнейшими геометрическими фигурами. Ученые придавали окружности большое значение, так как считали ее самой совершенной линией. Согласно Аристотелю, все планеты и звезды должны двигаться по окружности.
Это ошибочное мнение было опровергнуто около 400 лет назад. Самым важным элементом окружности древние ученые считали радиус. Слово радиус в переводе с латинского обозначает луч. В древности не было этого термина, использовали слова прямая от центра. Ученые древности утверждали, что из данной точки данным радиусом можно описать окружность. А сколько окружностей можно описать из одной точки с разными радиусами? (Из одной точки с разными радиусами можно описать много окружностей.)
Очень важное значение при усвоении понятий окружность и круг имеют задания, направленные на воспроизведение знаний и их применение. На этом этапе репродуктивные задания нужно заменить на задания творческие, эвристические. Ниже предлагаем несколько таких заданий.
1. Работа в парах. Ученики, сидящие за одной партой, составляют словесные портреты круга и окружности и читают их друг другу.
2. Сад «Окружностей и кругов». С помощью кругов и окружностей ученики должны нарисовать сказочный сад.
3. Геометрические орнаменты.
— Продолжите орнаменты на всю ширину тетради.

Придумайте свои орнаменты, где бы использовались круги, окружности или части из них.
4. Составление загадок о круге, об окружности.
5. Математическое исследование.
Ученикам предлагается выступить в роли ученого-исследователя. Надо: а) соединить отрезком две точки окружности таким образом, чтобы данный отрезок проходил и через центр окружности; б) написать выражение, по которому можно найти длину этого отрезка, если известен радиус окружности.
После выполнения данного задания учитель сообщает, что отрезок, который соединяет две точки окружности и проходит через центр, называется диаметром окружности (круга).
6. Как чертили в старину. Ученикам предлагается представить себе, что они попали в прошлое и им нужно нарисовать окружность, при условии, что циркуль еще не изобрели.
7. Разрежьте торт, верх которого имеет форму круга, на 4 равные части; на 8 равных частей.
8. Конкурс рисунков.
Класс делится на группы. Каждой группе предлагается «оживить» определенную геометрическую фигуру, закрасив ее разными цветами, чтобы с помощью созданного образа каждый почувствовал смысл оживляемой геометрической фигуры. Готовые работы ученики комментируют, обсуждают.
9. Догадайся, как можно начертить две окружности, чтобы они:
а) не имели общих точек;
б) имели одну общую точку;
в) имели две общие точки.
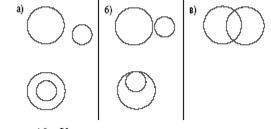
Это задание можно предложить учащимся для групповой работы. Для ее проверки ученики получают листы со следующими рисунками:
10. Как могут располагаться относительно друг друга окружность и прямая?
Начерти различные случаи. (Окружность и прямая могут: а) не иметь общих точек; б) иметь одну общую точку; в) иметь две общие точки.)
Интересные задания при изучении темы «Окружность и круг» предлагает профессор Н.Б. Истомина в своем учебнике «Математика. 2 класс».
1) Можно ли провести окружность с центром в точке О так, чтобы она проходила через точки А, В, С, D?
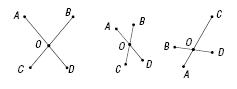
2) Догадайся! Через какие точки будет проходить окружность:
а) с центром в точке О;
б) с центром в точке С;
в) с центром в точке D?
Проверь свой ответ.
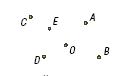
Для проведения практических работ при изучении темы «Окружность и круг» можно воспользоваться заданиями из тетради «Наглядная геометрия. 3 класс», авторы Н.Б. Истомина и Н.С. Подходова.
ПРИМЕРНАЯ СВОДНАЯ ТАБЛИЦА "ИЗУЧЕНИЕ ГЕОМЕТРИЧЕСКОГО МАТЕРИАЛА В ПРОГРАММАХ ДЛЯ НАЧАЛЬНОЙ ШКОЛЫ".
| Традиционная система (математика М.И.Моро и др.) | Математика Л.С.Петерсон | Математика Н.Б.Истоминой | Математика Н.Г.Салминой, В.А.Тарасова. |
| 1 класс. Сравнение предметов по размеруи форме. Числа от 1 до 10. Точка. Линии: кривая, прямая, отрезок,ломаная. Многоугольники. углы, вершины, стороны мно- гоугольника. Длина отрезка, сантиметр. Числа от 1 до 20. См и дм, их соотношение. | 1 класс. Общие понятия. Срав- нение предметов по цвету, форме, размеру, материалу. Распознавание геометрических фигур: квадрат, прямоугольник, треугольник, круг, шар, цилиндр, конус, пирамида, парал лелепипед, куб. Сравнение и раскраска фигур, составление фигур из частей и разбиение их на части. Фигуры на клетчатой бумаге. Подсчет числа клеток треугольников, прямоу- гольников на которые разбита фигура. Конструирование фигур из палочек. Точки и линии. Замкнутые и незамкнутые линии. Области и границы. Отрезок. Ломаная. Многоугольник, его вершины и стороны. Величины: длина, масса, объем и их измерение в древности и в наши дни (см, дм, кг, метр). | 1 класс. В разделах: "Признаки предметов", "Отношение", "Число и цифра". Дети знакомятся с фигурами: круг, треугольник, квадрат, куб; сравниваются их форма, цвет, размер. │ Точка. Прямая и кривая линии. Луч. Замкнутые линии, пересечение линий. Отрезок. Сравнение отрезка по длине, измерение отрезка разными мерками с помощью циркуля. Сравнение длин отрезков, сложение и вычитание отрезков с помощью циркуля. Ломоная линия, ее звенья. Нахождение длины ломаной. Угол. Виды углов. Прямоугольник и квадрат. Многоугольники. Знакомство с периметром прямоугольника (как сложением длин сторон прямоу гольника). Знакомство с симметричными фигурами. | 1 класс. Сравнение по различным признакам. Измерения величин. |
| 2 класс. Числа от 1 до 100. Длина ломаной. См, дм и м. Соотношение между ними. _Внетабличное сложение и вычитание. Углы прямые и непрямые. Прямоугольник. Свойства противоположных сторон прямоугольника, квадрат. Построение прямого угла прямоугольника (квадрата) на клетчатой бумаге. | 2 класс. Метр, сравнение, сложение и вычитание именован- ных чисел. Аналогия десятичной записи чисел и десятичной системы мер, сети линий. Пути. Прямая. Луч. Отрезок. Ломаная, длина ломаной. Периметр многоугольника. Плоскость. Угол. Прямой угол. Прямоугольник. Квадрат. Площадь фигуры и ее измерение. Единицы площади: см кв., дм кв., м кв. Площадь прямоугольника. Куб, его ребра и грани. Единицы объема: см куб., дм куб., м куб. Прямоугольный параллелепипед. Объем прямоугольного параллелепипеда. Круг и окружность. Циркуль. Вычерчивание узоров из гео- метрических фигур. Монеты и купюры. | 2 класс (1-3). Подготовка к изучению периметра любого многоугольника. Нахождение периметра прямоугольника и длины ломаной. Площадь фигуры. Сравнение площадей фигур наложением. Перестройка, перекроение фигур. Измерение площади фигур с использованием различных мерок. Сравнение площадей различных фигур. Введение общепризнанных единиц измерения площади: см кв., дм кв., м кв. Измерение площади с помощью палетки. Формулы нахождения S и P прямоугольника. Решение задач. Построение симметричных фигур относительно прямой (точки, отрезка, другой фигуры). Подсчет количества кубиков, из которых состоит фигура. | 2 класс. 1. Выделение пространственных отношений между объектами, направления (влево, вправо, вверх, вниз, осевая симметрия). 2. Обозначение положения объекта на плоскости. 3. Прямая. Отрезок. Длина отрезка. Единицы длины. Соотношение единиц длины. Ломаная, ее звенья. Длина ломаной. Треугольник, его периметр. Многоугольник. Разрезание на части геометрических фигур. 4. Нестандартные задачи ( танграм, пентамино). Конструирование объектов по образцу. 5. Задачи на раскрашивание фигур, выделение границ. |
| 3 класс. Таблица умножения и деления. Единицы длины: мм, см, дм, м. Соотношение между ними. Обозначение геометрических фигур буквами. Длина ломаной. Периметр прямоугольника. Виды треугольников: разносторонний, равнобедренный (равносторонний). Периметр прямоугольника (квадрата). Площадь. Единицы площади: мм кв., см кв., дм кв. Соотношение между ними. Площадь прямоугольника (квадрата). Круг, окружность, центр, радиус. Единицы времени: месяц, сутки. Соотношение между ними. Единицы массы: кг, гр. Соотношение между ними. | 3 класс. Км, мм, грамм, центнер, тонна. Сравнение, сложение и вычитание именованных чисел. Переход от одной единицы измерения к другой. Измерение времени. Единицы измерения времени: год, сутки, час, минута, секунда. Определение времени по часам. Название месяцев и дней недели. Календарь. Соотношение между единицами измерения времени. Раскраска и перегибание фигур. Преобразование фигур на плоскости. Симметрия фигур. Объединение и пересечение фигур. | 3 класс. Знакомство с телами: призмы, конус, цилиндр, пирамиды. Их особенности, сравнение. Нахождение S сложных фигур (разбиением их на прямоугольники и квадраты). Знакомство с развертками тел: куба, треугольной и четырехугольной призмы, пирамиды. Окружность, центр окружности. Круг, радиус круга. Построение окружности, симметричной данной относительно прямой. Понятие объема. Единицы измерения объема: 1 см куб., 1дм куб. | 3 класс. 1. Положение и обозначение объекта на плоскости. 2.Симметрия: осевая и центральная. 3.Раскрашивание фигур, выделение границ. 4.Типы криволинейных геометрических фигур на плоскости. (круг, окружность, полукруг, кольцо, овал). 5.Простые геометрические фигуры и тела в пространстве: куб, параллелепипед. Развертки. 6.Простейшие геометрические задачи на плоскости: - на вычисление периметра; - на построение; 7.Нестандартные задачи. |
| 4 класс. Нумерация. Луч. Угол. Виды углов: прямой, острый, тупой. Величины. Единицы длины: км, м, дм, см, мм. Соотношение между ними. Единицы площади: мм кв., см кв., дм кв., м кв., км кв. Соотношение между ними. Единицы массы: т, ц, кг, грамм. Соотношение между ними. Единицы времени: век, год, месяц, сутки, час, минута, секунда. Соотношение между ними. Сложение и вычитание. Треугольник. Виды треугольников: прямоугольный, остроугольный, тупоугольный. Умножение и деление. Площадь прямоугольного треугольника, на которые разбит прямоугольник. Площадь фигур, которые могут быть разбиты на прямоугольные треугольники. В течение года проводится: решение задач на узнавание геометрических фигур в составе более сложных; разбиение фигур на заданные части; составление заданных фигур из 2-3 ее частей; изображение знакомых фигур на клетчатой и на нелинованой бумаге с помощью линейки, чертежного треугольника и циркуля. | 4 класс. Прямоугольный треугольник, его стороны и площадь. Оценка площади. Приближенное вычисление площадей. Новые единицы площади: ар, гектар. Действия с составными именованными числами. Измерение углов. Транспортир. Развернутый угол. Смежные и вертикальные углы. Исследование свойств геометрических фигур с помощью измерений. | 4 класс. 1. Положение и обозначение объекта (точки) на плоскости. Введение прямоугольной системы координат. Задачи на систему координат. 2. Симметрия (осевая и центральная). Примеры симметричных фигур. Задачи. 3.Раскрашивание фигур, Выделение границ (в том числе у прямолинейных фигур). 4.Понятие площади. Единицы площади. Площадь квадрата, прямоугольника. Равновеликие фигуры. Площадь равновеликих фигур. 5.Простейшие геометрические фигуры и тела в пространстве. Развертка. 6. Простейшие геометрические задачи: на периметр, площадь (построение прямоугольника по периметру и одной стороне, площади и одной стороне на клетчатой основе). |