Кривые 2 порядка
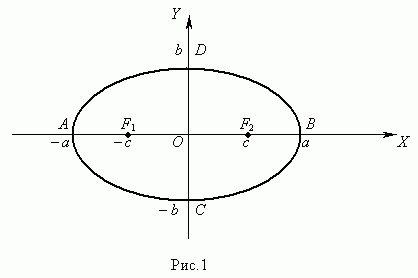
Уравнение эллипса ( рис.1 ) :
Здесь начало координат является центром симметрии эллипса, а оси координат – его осями симметрии. При a > b фокусы эллипса лежат на оси ОХ ( рис.1 ) , при a < b фокусы эллипса лежат на оси ОY , а при a = b эллипс становится окружностью ( фокусы эллипса в этом случае совпадают с центром окружности ). Таким образом, окружность есть частный случай эллипса.
Отрезок F1F2 = 2 с , где , называется фокусным расстоянием. Отрезок AB = 2 a называется большой осью эллипса, а отрезок CD = 2 b – малой осью эллипса. Число e = c / a , e < 1 называется эксцентриситетом эллипса.
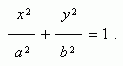
Гипербола. Гиперболой называется геометрическое место точек, разность расстояний которых от двух данных фиксированных точек (фокусов) гиперболы есть одна и та же постоянная величина. Предполагается, что эта постоянная величина не равна нулю и меньше, чем расстояние между фокусами.
Простейшее уравнение гиперболы
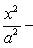
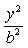
Здесь a - действительная полуось гиперболы, b - мнимая полуось гиперболы.
Если 2c - расстояние между фокусами гиперболы, то между a, b и c существует соотношение
a2 + b2 = c2.
При b = a гипербола называется равносторонней. Уравнение равносторонней гиперболы имеет вид
x2 - y2 = a2.
Фокусы гиперболы лежат на ее действительной оси.
Эксцентриситетом гиперболы называется отношение расстояния между фокусами этой гиперболы к длине ее действительной оси.
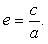
Парабола. Параболой называется геометрическое место точек, каждая из которых одинаково удалена от заданной фиксированной точки и от заданной фиксированной прямой. Точка, о которой идет речь в определении, называется фокусом параболы, а прямая - ее директрисой.
Простейшее уравнение параболы
y2 = 2px. (*)
Входящая в это уравнение величина p называется параметром параболы. Параметр параболы равен расстоянию от директрисы параболы до ее фокуса.
Координаты фокуса F параболы 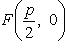 (*) . (фокус параболы лежит на ее оси симметрии) Уравнение директрисы параболы (*)
(*) . (фокус параболы лежит на ее оси симметрии) Уравнение директрисы параболы (*)
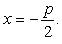
Эксцентриситет параболы e = 1.
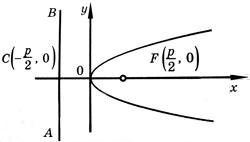
y2 = 2px (p > 0)