Фракталы

 

1 Определение понятия «фрактал».

Фрактал (лат. fractus — дроблёный, сломанный, разбитый) – это геометрическая фигура, обладающая свойством самоподобия, то есть составленная из нескольких частей, каждая из которых подобна всей фигуре целиком.

Фракталам характерна геометрическая «изрезанность». Поэтому используется специальное понятие фрактальной размерности. Размерность Хаусдорфа - Безиковича позволяет измерять степень «изрезанности». Размерность фрактальных объектов не является целым числом, характерным для привычных геометрических. Вместе с тем, в большинстве случаев фракталы напоминают объекты, плотно занимающие реальное пространство, но не использующие его полностью.

Пусть есть множество G в евклидовом пространстве размерности d_τ. Это множество покрывается кубиками размерности d_τ, при этом длина ребра любого кубика не превышает некоторого значения δ, т.е. d_τ < δ.

Вводится зависящая от некоторого параметра d и δ сумма по всем элементам покрытия: .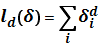

Определим нижнюю грань данной суммы: .

При уменьшении максимальной длины δ, если параметр d будет достаточно велик будет выполняться: .

При некотором достаточно малом значении параметра d будет выполняться:.

Промежуточное, критическое значение d_x, для которого выполняется:называется размерностью Хаусдорфа-Безиковича (или фрактальной размерностью).

 

Выделяют 3 класса фракталов:

Геометрические (конструктивные)

Динамические (алгебраические)

Стохастические (случайные)

 

2.1 Геометрические фракталы

Геометрическими называются фракталы, форма которых может быть описана как последовательность простых геометрических операций. Геометрические фракталы строятся на основе исходной фигуры, называемой генератором (линии, многоугольника, многогранника) путем ее дробления и выполнения логических преобразований полученных фрагментов. В результате бесконечного повторения этой процедуры, получается геометрический фрактал.

 

Треугольник Серпинского:

Чтобы его получить, нужно взять (равносторонний) треугольник с внутренностью, провести в нём средние линии и выкинуть центральный из четырех образовавшихся маленьких треугольников. Дальше эти же действия нужно повторить с каждым из оставшихся трех треугольников, и т. д.

 

Динамические фракталы – это фракталы, которые возникают при исследовании динамических систем.

Множество Мандельброта

Данная фрактальная структура получается путем многократного применения алгебраического преобразования с использованием функции комплексного переменного.

Визуально множество Мандельброта выглядит как набор бесконечного количества различных фигур, самая большая из которых называется кардиоидой. Кардиоида окружена всё уменьшающимися кругами, каждый из которых окружен еще меньшими кругами, и т. д. до бесконечности.

 

2.3 Стохастические фракталы

Получаются в том случае, если в итерационном процессе случайным образом менять какие-либо его параметры. При этом получаются объекты очень похожие на природные - несимметричные деревья, изрезанные береговые линии и т.д. Двумерные СФ используются при моделировании рельефа местности и поверхности моря. Примерами стохастических фракталов являются фрактальные кривые, возникающие в критических двумерных моделях статистической механики.

3 Природные фракталы

Природные объекты обладают одним общим свойством структуры – они самоподобны.

Примеры фракталов, встречающихся в природе – молния, облака, деревья, кровеносные сосуды.

4 Применение фракталов

Естественные науки

В физике фракталы возникают при моделировании нелинейных процессов (течение жидкости, пламя, облака).

В нефтехимии фракталы используются при моделировании пористых материалов.

В биологии они применяются для моделирования популяций и для описания систем внутренних органов.

Радиотехника – выпускаются антенны фрактальной формы: обеспечивают качественный прием сигнала, занимая мало места.

Экономика и финансы

В последнее время «трейдеры» используют фракталы для анализа курса фондовых, валютных и торговых бирж.

Информатика

- Сжатие изображений

- Компьютерная графика

- Децентрализованные сети

5 Фрактальное искусство

Фрактальное искусство – это форма алгоритмического искусства, созданного с помощью вычисления фрактальных объектов и представления результатов вычислений в виде изображений, анимаций и медиа-файлов.

Фрактальное искусство не рисуется вручную. Обычно оно создается с помощью программного обеспечения для генерации фракталов.