условия совместности (неразрывности) деформаций Сен-Венана.

 

Коренным образом изменяется физический закон, отражающий функциональную связь между деформациями и напряжениями в точке твердого тела.

Простейшая запись физического закона (закон Гука) для одноосного нагружения изотропного тела имеет вид

(5.1)

σ – напряжение, обуславливающее эту деформацию;

Е– модуль упругости (модуль Юнга).

Объектами исследования механики деформируемого твердого тела являются в общем случае изотропные и анизотропные среды с однородной (гомогенной) и неоднородной (гетерогенной) структурами.

Изотропное тело обладает одинаковыми физико-механическими свой­твами по всем направлениям.

Изотропными с большой степенью приближения являются металлы, пластмассы, стекло и другие материалы.

Анизотропное тело характеризуется различными свойствами в разных направлениях. Примерами таких сред являются древесный шпон, однонаправленные и сложноармированные КМ, упругие и прочностные свойства которых зависят от направления вырезки образца из листа по отношению к направлению волокон шпона или КМ.

 

Рисунок 5.2 – Деформированное состояние анизотропного тела

 

Многие анизотропные тела обладают некоторой симметрией свойств относительно какой-либо оси (рис. 5.2, а).

В общем случае, если через тело можно провести три ортогональные плоскости, относительно которых физико-механические свойства материала обладают симметрией, то такое тело называется ортотропным.

Понятие ортотропии связано с конкретной системой координат, без указания которой само понятие не имеет смысла, например, однонаправленный КМ (рис. 5.2, а) в осях х, у является ортотропным, а в осях х1, у1 – анизотропным.

Учитывая, что КМ используются в основном для изготовления пластин, панелей, обшивок и т.п. и в целях обеспечения большей доступности теоретических выкладок, в дальнейшем будут рассматриваться плоские тела, для которых самыми важными являются физико-механические свойства в плоскости.

На рис. 5.2, б показаны общепринятые обозначения напряжений и деформаций, а также их положительные направления.

Уравнения физического закона для такого анизотропного тела имеют вид

(5.2)

где Ex, Ey, Gxy – модули упругости материала на растяжение – сжатие по осям х и у, а также на сдвиг в плоскости xy;

μχγ μγχ – коэффициенты Пуассона, причем первый индекс указывает на направление действия нормальных напряжений, а второй - на направлениение поперечной деформации;

ηх, ху, ηу, ху – коэффициенты взаимного влияния первого рода, характеризующие степень деформируемости тела на сдвиг от действия нормальных напряжений (рис. 5.2, в);

ηху, х, ηху, у – коэффициенты взаимного влияния первого рода, харакризующие степень деформируемости тела по осям χ и у от действия касательных напряжений (рис. 5.2, г).

В механике деформируемого твердого тела имеется доказательство положения о том, что коэффициенты взаимного влияния первого рода ортотропного в осях х, у тела равны нулю. Тогда уравнения примут более простую форму

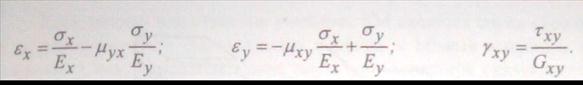(5.3)

Из уравнений (5.2) и (5.3) видно, что, для того чтобы определить деформации тела по известным напряжениям, необходимо знать величины модулей упругости Ex,Ey,Gxy, коэффициентов Пуассона μχγ μγχ и коэффициентов взаимного влияния первого рода r ηх, ху, ηу, ху, ηху, х, ηху, у которые для линейно деформируемых тел считаются независимыми от напряжений. По этой причине их называют упругими константами материала.

Из постулата о наличии упругого потенциала деформируемого твердого тела следуют равенства:

(5.4)

С учетом этих уравнении анизотропное плоское тело можно охарактеризовать шестью независимыми упругими константами, которые необходимо уметь прогнозировать для известных компонентов и структуры КМ.

В общем случае методика прогнозирования физико-механических свойств КМ сводится к двум взаимосвязанным задачам:

– определение свойств однонаправленного КМ в осях 1,2 (рис. 5.3, а);

– определение физико-механических свойств пакета однонаправленных слоев с произвольными углами ориентации относительно осей х, у (рис. 5.3, б).

Для слоистого КМ, состоящего из произвольного количества однонаправленных слоев с углами армирования φi где (положительные направления углов (φi соответствуют повороту от оси χ до оси 1 против часовой стрелки) (рис. 5.3, в), введем глобальную систему координат х, у и местную 1, 2 (рис. 5.3, в).

Рисунок 5.3 – К постановке задачи прогнозирования свойств КМ

Так как в осях 1, 2 каждый слой является ортотропным, то уравнения физического закона для каждого слоя имеют вид

Где E1i, E2i – модули упругости слоя вдоль и поперек волокон соответственно;

G12i – модуль сдвига слоя в осях 1,2;

коэффициенты Пуассона.

Так как

то для каждого слоя необходимо определить четыре упругие константы: E1, E2, G12, μ12.

В дальнейшем понадобятся формулы пересчета напряжений и деформаций при переходе от системы координат х, у к осям 1, 2 и наоборот, которые имеют вид

Вся лекция по «Проектированию деталей и агркгатов из КМ» Я. С. Карпова