Пример решения задачи 2

Для примера рассмотрим манипулятор, изображенный на рис. 5.

Звенья механизма обозначим арабскими цифрами, количество их n = 5.

Кинематические пары, входящие в состав данного механизма:

p₅ = 3, в том числе две вращательные (А, В) и одна поступательная (С);

р₄ = 2, сферический шарнир с пальцем ( Д ) и цилиндрическая пара (В). До тех пор, пока захват (звено 5) не соединяется с объектом манипулирования, кинематическая цепь является незамкнутой.

Определяем степень подвижности:

W = 6 × 5 - 5×4 - 4×2 = 7

Таким образом, механизм имеет 7 независимых движений для ориентации и перемещения в рабочем пространстве.

После того, как захват подведен к объекту манипулирования и объединен с ним, количество подвижных звеньев становится на единицу меньше, т.е. n = 4. Число кинематических пар остается неизменным. Теперь можно определить маневренность манипулятора.

 

 

 

 

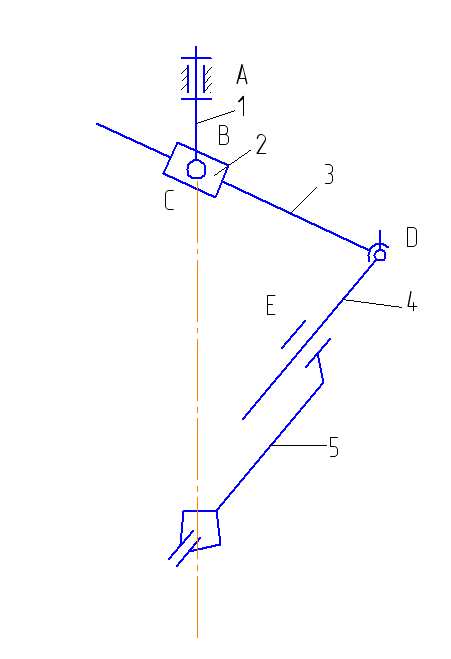Рис. 5. Структурная схема руки манипулятора

W = 6×5 - 5×3 - 4×2 = 1

 

Тот факт, что маневренность равна единице, означает, что при фиксированном положении захвата (неподвижная точка В) звенья механизма могут менять свое положение в зависимости от положения одного из звеньев: например, при вращении звена 2 одновременно изменятся длины сторон ВД и ДЕ, а также углы треугольника ВДЕ, то есть положение звеньев 3 и 4 является функцией угла поворота звена 2.