Примеры решения задач

1 Пользуясь теорией Бора, выведите формулы для потенциальной, кинетической и полной энергии электрона, движущегося по -й орбите в водородоподобном атоме.

 

Дано: Z, n Найти: Un-? Tn-? En-? Решение Потенциальная энергия электрона в водородоподобном атоме, порядковый номер которого в Периодической системе элементов Д. И. Менделеева равен Z, определяется электростатическим взаимодействием электрона и ядра, которые можно считать точечными зарядами: . (2.10)

Здесь – расстояние между электроном и ядром (радиус -ой круговой орбиты электрона).

Кинетическая энергия электрона определяется по формуле

, (2.11)

где – скорость электрона на - ой орбите.

Для того, чтобы определить радиус 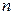- й орбиты и скорость электрона , необходимо решить систему из уравнений (2.3), (2.4):

,

.

Получим:

, (2.12)

. (2.13)

Подставляя (2.12) в формулу (2.10), а (2.13) – в формулу (2.11), получим следующие выражения для потенциальной и кинетической энергии электрона, движущегося по 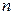-й орбите:

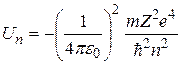, (2.14)

. (2.15)

Суммируя (2.14) и (2.15), получим выражение для полной энергии электрона, находящегося в 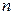-м стационарном состоянии:

.

Ответы: , ,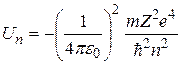

.

Дано: Eф=16,5 эВ =26,4·10-19 Дж n=1 Решение Для того чтобы определить скорость выбитого из атома электрона, воспользуемся законом сохранения энергии для рассматриваемого явления. Получив энергию Eф,электрон, находящийся в невозбужденном состоянии (n=1) атома водорода ( ), преодолеет притяжение с ядром, т.е. потратит энергию и, покинув атом, приобретет кинетическую энергию :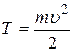
Найти: -?

2Фотон с энергией 16,5 эВ выбил электрон из невозбужденного атома водорода. Какую скорость будет иметь электрон вдали от ядра атома?

(2.16)

В соответствии с теорией Бора энергия водородоподобной системы в n-м стационарном состоянии определяется по формуле (2.6). При условиях , n=1 она приобретает вид

.

Затратив энергию связи, электрон станет свободным, т.е. его энергия станет равной нулю. Следовательно,

. (2.17)

Подставляя (2.17) в формулу (2.16) и выражая затем скорость, получим:

.

В результате вычислений определим значение скорости электрона: 1,01·106 м/с.

 

Ответ: 1,01·106 м/с.

 

2 Атомарный водород возбуждают на n-й энергетический уровень. Определить длины волн испускаемых линий, если n = 4; каким сериям принадлежат эти линии?

 

Дано: n =4 Решение Различные атомы водорода, находящиеся в зоне возбуждения и переведенные в возбужденное состояние с n = 4, могут вернуться в основное состояние (n = 1), совершая последовательность различных квантовых переходов.
Найти: -?

Воспользуемся схемой энергетических уровней, изображенной на рисунке 2.1, и укажем все возможные последовательности квантовых переходов, совершая которые атомы водорода могут перейти с возбужденного уровня (n = 4) на основной (n = 1):

а) 4→3; 3→2; 2→1;

б) 4→2; 2→1;

в) 4→3; 3→1;

г) 4→1.

Выпишем неповторяющиеся квантовые переходы:

4 → 3 ( ); 3 → 2 ( ); 2 → 1( ) ;

4 → 2 ( ); 3 → 1 ( ); 4 → 1 . ( ) . (2.18)

 

Выразим длины волн спектральных линий, соответствующих всем указанным квантовым переходам, пользуясь обобщенной формулой Бальмера (2.1) и связью между волновым числом и длиной волны излучения :

; ; .

(2.19)

Длины волн , , выразим, применяя комбинационный принцип Ритца:

; ;

. (2.20)

Вычислим значений длин волн , , , , по формулам (2.19), (2.20), учитывая значение постоянной Ридберга ( м-1).

Получим: м.

Устанавливая соответствие спектральных линий различным квантовым переходам (2.18) определим, что спектральная линия с длиной волны м относится к серии Пашена; линии с длинами волн м и м – серии Бальмера; м, м и м – серии Лаймана.

Ответ: м (серия Пашена); м, м (серия Бальмера); м, м, м (серия Лаймана).