Вынужденные колебания с торможением. Электрический резонанс. Энергия осциллятора.

 

Итак, мы можем решить задачу о колебательном движении, пользуясь изящной математикой. Однако изящество немногого стоит, когда задача и так решается просто; математику надо использовать тогда, когда решаются более сложные задачи. Перейдем поэтому к одной из таких задач, которая, кроме того, ближе к действительности, чем предыдущая. Из уравнения (23.5) следует, что, если 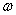в точности равна 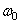, амплитуда колебания становится бесконечной. Этого, конечно, не может быть, потому что многие вещи, например трение, ограничивают амплитуду, а мы их не учитывали. Изменим теперь (23.2) так, чтобы учесть трение.

Сделать это обычно довольно трудно, потому что силы трения очень сложны. Однако во многих случаях можно считать, что сила трения пропорциональна скорости движения объекта. Именно такое трение препятствует медленному движению тела в масле или другой вязкой жидкости. Когда предмет стоит на месте, на него не действуют никакие силы, но чем скорее он движется и чем быстрее масло должно обтекать этот предмет, тем больше сопротивление. Таким образом, мы предположим, что в (23.2), кроме уже написанных членов, существует еще один - сила сопротивления, пропорциональная скорости: . 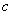Удобно записать как произведение на другую постоянную ; это немного упростит уравнение.

Мы уже проделывали такой фокус, когда заменяли на , чтобы упростить вычисления. Итак, наше уравнение имеет вид

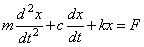, (23.6)

или, если положить и и поделить обе части на ,

. (23.6а)

Это самая удобная форма уравнения. Если очень мало, то мало и трение, и, наоборот, большие значения соответствуют громадному трению. Как решать это новое линейное уравнение? Предположим, что внешняя сила равна ; можно было бы подставить это выражение в (23.6а) и попытаться решить полученное уравнение, но мы применим наш новый метод. Представим как действительную часть , а - как действительную часть и подставим эти комплексные числа в (23.6а). Собственно говоря, и подставлять-то нечего; внимательно посмотрев на (23.6а), вы тут же скажете, что оно превратится в

. (23.7)

[Если бы мы попытались решить (23.6а) старым прямолинейным способом, то оценили бы по достоинству магический «комплексный» метод.] Поделив обе части уравнения на 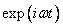, найдем отклик осциллятора на силу .

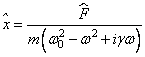. (23.8)

Итак, отклик равен силе , умноженной на некоторый множитель. Этот множитель не имеет ни названия, ни какой-то своей собственной буквы, и мы будем обозначать его буквой :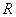

;

тогда

. (23.9)

Этот множитель можно записать либо как , либо как . Запишем его в виде и посмотрим, к чему это приведет. Внешняя сила - это действительная часть числа 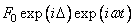, она равна . Уравнение (23.9) говорит нам, что отклик равен ; мы условились писать 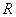в виде ; следовательно,

.

Вспомним (об этом уже говорилось), что физическое значение , равное действительной части комплексного числа , равно действительной части . Но и - действительны, а действительная часть - это просто . Таким образом,

. (2.3.10)

Это значит, что амплитуда отклика равна амплитуде силы , умноженной на коэффициент усиления ; мы нашли «размах» колебаний. Но это еще не все: видно, что колеблется не в такт с силой; фаза силы равна , а у она сдвинута на дополнительную величину . Следовательно, и - это величина и фазовый сдвиг отклика.

Найдем теперь значение . Квадрат модуля любого комплексного числа равен произведению этого числа на комплексно сопряженное, т. е.

. (23.11)

Можно найти и фазовый угол

;

значит,

. (23.12)

Знак минус возник оттого, что . Угол отрицателен при всех значениях 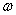, т. е. смещение отстает по фазе от силы .

На рис. 23.2 показано, как изменяется при изменении частоты ( для физика интереснее, чем , потому что пропорционально квадрату амплитуды, а значит, и той энергии, которую передает осциллятору внешняя сила). Очевидно, что если мало, то основной член в (23.11) - это , и отклик стремится к бесконечности, если 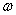приближается к 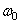. Но эта «бесконечность» - не настоящая бесконечность, потому что даже если , то все еще остается слагаемое . Зависимость сдвига фазы от частоты изображена на рис. 23.3.

Рис. 23.2. График зависимости от .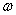

Рис. 23.3. График зависимости от .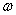

Иногда приходится иметь дело с формулой, немного отличающейся от (23.8); она тоже называется «резонансной» и, несмотря на некоторое отличие от (23.8), описывает те же самые явления. Дело в том, что если значение очень мало, то наиболее интересная область резонансной кривой лежит около частоты , а здесь при малых формулу (23.8) с большой степенью точности можно заменить приближенной формулой. Поскольку , то для 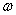, очень близких к 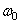, разность квадратов почти равна , а можно заменить на . Значит, и

, если и . (23.13)

Легко найти и :

.

А теперь решите сами такую задачу: с увеличением частоты значение сначала растет, достигает при 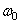максимума, а потом снова убывает. На каком расстоянии от 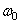расположены частоты, которым соответствуют значения , вдвое меньшие максимального? Покажите, что при очень малом эти точки отстоят друг от друга на расстояние . Это значит, что резонанс делается более острым по мере того, как влияние трения становится все слабее и слабее.

Другой мерой ширины резонанса может служить «добротность» (чем уже резонанс, тем больше ); если , то по шкале частот ширина резонансной кривой равна всего 0,001. Резонансной кривой на рис. 23.2 соответствует .

Явление резонанса важно потому, что оно проявляется довольно часто; описанию некоторых видов этих проявлений мы посвятим остаток главы. Простейшие и самые широкие технические применения резонанс нашел в электричестве. Имеется довольно много устройств, из которых собираются электрические цепи. Их часто называют пассивными элементами цепи, и бывают они трех типов, хотя в каждый элемент одного типа всегда примешано чуточку элементов других типов. Прежде чем подробно описать эти элементы, заметим, что наше представление о механическом осцилляторе как о массе, подвешенной к концу пружины, всего лишь приближение. В «массе» сосредоточена вовсе не вся масса системы: пружина тоже обладает какой-то массой, пружина тоже инерционна. Точно так же «пружина» не состоит из одной пружины, масса тоже немного упруга, а не абсолютно тверда, как это может показаться. Подпрыгивая вверх и вниз, она слегка изгибается под толчками пружины. Так же обстоит дело и в электричестве. Расположить все предметы по «элементам цепи» с чистыми, идеальными характеристиками можно только приближенно. Так как у нас нет времени обсуждать пределы таких приближений, мы просто предположим, что они допустимы.

Итак, о трех элементах цепи. Первый называется емкостью (рис. 23.4); в качестве примера емкости могут служить две металлические пластинки, разделенные тонким слоем диэлектрика. Если пластинки зарядить, то между ними возникает разность потенциалов. Та же самая разность потенциалов будет между точками А и B, потому что при любой дополнительной разности потенциалов вдоль соединительных проводов заряды стекут по проводам. Таким образом, заданной разности потенциалов между пластинками соответствуют определенные заряды и на каждой пластинке. Между пластинками существует некое электрическое поле; мы даже вывели соответствующую формулу для него (см. гл. 13 и 14)

, (23.14)

где - расстояние между пластинками, - площадь пластинок. Заметим, что разность потенциалов линейно зависит от заряда. Если построить емкость не из параллельных пластин, а придать отдельным электродам какую-нибудь другую форму, разность потенциалов будет по-прежнему пропорциональна заряду, но постоянную пропорциональности не так-то легко будет рассчитать. Однако надо знать только одно: разность потенциалов между концами емкости пропорциональна заряду ; множитель пропорциональности равен ( и есть емкость объекта).

Рис. 23.4. Три пассивных элемента цепи.

Второй элемент цени называется сопротивлением; этот элемент оказывает сопротивление текущему через него электрическому току. Оказывается, что все металлические провода, а также многие другие материалы сопротивляются току одинаково; если к концам куска такого материала приложить разность потенциалов, то электрический ток в куске будет пропорционален приложенной разности потенциалов

. (23.15)

Коэффициент пропорциональности называют сопротивлением 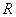. Соотношение между током и разностью потенциалов вам, наверное, уже известно. Это закон Ома.

Если представлять себе заряд, сосредоточенный в емкости, как нечто аналогичное смещению механической системы , то электрический ток аналогичен скорости, сопротивление 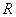аналогично коэффициенту сопротивления , а аналогично постоянной упругости пружины . Самое интересное во всем этом, что существует элемент цепи, аналогичный массе! Это спираль, порождающая внутри себя магнитное поле, когда через нее проходит ток. Изменение магнитного поля порождает на концах спирали разность потенциалов, пропорциональную . (Это свойство спирали используется в трансформаторах.) Магнитное поле пропорционально току, а наведенная разность потенциалов (так ее называют) пропорциональна скорости изменения тока

. (23.16)

Коэффициент - это коэффициент самоиндукции; он является электрическим аналогом массы.

Предположим, мы собираем цепь из трех последовательно соединенных элементов (рис. 23.5); приложенная между точками 1 и 2 разность потенциалов заставит заряды двигаться по цепи, тогда на концах каждого элемента цепи тоже возникает разность потенциалов: на концах индуктивности , на сопротивлении , а на емкости . Сумма этих напряжений дает нам полное напряжение :

. (23.17)

Мы видим, что это уравнение в точности совпадает с механическим уравнением (23.6); будем решать его точно таким же способом. Предположим, что осциллирует; для этого надо соединить цепь с генератором синусоидальных колебаний. Тогда можно представить как комплексное число , помня, что для определения настоящего напряжения это число надо еще умножить на 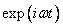и взять действительную часть. Аналогично можно подойти и к заряду , а поэтому напишем уравнение, в точности повторяющее (23.8): вторая производная - это , а первая - это . Уравнение (23.17) перейдет в

, или ;

последнее равенство запишем в виде

, (23.18)

где , а . Мы получили тот же знаменатель, что и в механической задаче, со всеми его резонансными свойствами! В табл. 23.1 приведен перечень аналогий между электрическими и механическими величинами.

Таблица 23.1 Механические и электрические величины

Общие характеристики	Величины
механические	электрические
Независимая переменная	Время	Время
Зависимая переменная	Положение	Заряд
Инерция	Масса	Индуктивность
Сопротивление	Коэффициент трения	Сопротивление
Жесткость	Жесткость	(Емкость)-1
Резонансная частота
Период
Добротность

Рис. 23.5. Электрический колебательный контур, состоящий из сопротивления, индуктивности и емкости

Еще одно чисто техническое замечание. В книгах по электричеству используют другие обозначения. (Очень часто в книгах на одну и ту же тему, написанных людьми разных специальностей, используются различные обозначения.) Во-первых, для обозначения используют букву , а не 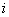(через 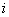должен обозначаться ток!). Во-вторых, инженеры предпочитают соотношение между и , а не между и . Они так больше привыкли. Поскольку , то вместо можно подставить , и тогда

. (23.19)

Можно слегка изменить исходное дифференциальное уравнение (23.17), чтобы оно выглядело более привычно. В книгах часто попадается такое соотношение:

. (23.20)

Во всяком случае, мы находим, что соотношение (23.19) между напряжением и током то же самое, что и (23.18), и отличается только тем, что последнее делится на . Комплексное число инженеры-электрики часто называют особым именем: комплексный импеданс . Введение новой буквы позволяет просто записать соотношение между током и сопротивлением в виде . Объясняется это пристрастие инженеров тем, что в юности они изучали только цепи постоянного тока и знали только сопротивления и закон Ома: . Теперь они более образованы и имеют уже цепи переменного тока, но хотят, чтобы уравнения были те же самые. Вот они и пишут и единственная разница в том, что теперь сопротивление заменено более сложной вещью: комплексным числом. Они настаивают на том, что они не могут использовать принятого во всем мире обозначения для мнимой единицы и пишут ; поистине удивительно, что они не требуют, чтобы вместо буквы писали букву 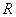! (Много волнений доставляют им разговоры о плотности тока; ее они тоже обозначают буквой . Сложности науки во многом связаны с трудностями в обозначениях, единицах и прочих выдумках человека, о чем сама природа и не подозревает.)

Чему равна кинетическая энергия осцил­лятора? Она пропорциональна квадрату скоро­сти. Здесь мы затронули важный вопрос. Пред­положим, что мы изучаем свойства некоторой величины А; это может быть скорость или еще что-нибудь. Мы обратились к помощи ком­плексных чисел: A==Âехр(iwt), но в физике праведна и чтима только действительная часть комплексного числа. Поэтому если вам для чего-нибудь понадобится получитьквадрат А, то не возводите в квадрат комплексное число, чтобы потом выделить его действительную часть.

Действительная часть квадрата комплексно­го числа не равна квадрату действительной ча­сти, она содержит еще и мнимую часть первона­чального числа. Таким образом, если мы захо­тим найти энергию и посмотреть на ее превра­щения, нам придется на время забыть о комп­лексных числах.

Итак, истинно физическая величина А — это действительная часть A₀exp[i(wt+D)], т. е.

A=A₀соs(wt+D), а комплексное число А — это j4oexp(iD). Квадрат этой физической величины равен A²₀cos²(wt+D). Он изменяется от нуля до максимума, как это предписывается квадра­том косинуса. Максимальное значение квадрата косинуса равно 1, минимальное равно 0, а его среднее значение — это ¹/₂.

Зачастую нас совсем не интересует энергия в каждый дан­ный момент колебания; во многих случаях достаточно знать лишь среднюю величину A² (среднее значение квадрата А в те­чение времени, много большего, чем период колебаний). При этих условиях можно усреднить квадрат косинуса и доказать теорему: если А представляется комплексным числом, то сред­нее значение А² равно ¹/₂A²₀. Здесь А²₀ — это квадрат модуля комплексного числа А. (Квадрат модуля Â записывают по-раз­ному;

|Â |² или ÂÂ *— в виде произведения числа Â на комплек­сно сопряженное.) Эта теорема пригодится нам еще много раз.

Итак, речь идет об энергии осциллятора, на который дейст­вует внешняя сила. Движение такого осциллятора описывается уравнением

Мы, конечно, предполагаем, что F(t) пропорциональна coswt. Выясним теперь, много ли приходится этой силе работать. Ра­бота, произведенная силой в 1 сек, т. е. мощность, равна произ­ведению силы на скорость. [Мы знаем, что работа, совершаемая за время dt, равна Fdx, а мощность равна F(dx/dt).] Значит,

Как легко проверить простым дифференцированием, первые два члена можно переписать в виде (d/dt)][^l/₂m(dx/dt)²+¹/₂mw²x²]. Выражение в квадратных скобках — производная по времени суммы двух членов. Это понятно; ведь первый член суммы — кинетическая энергия движения, а второй — потенциальная энергия пружины. Назовем эту величину запасенной энергией, т. е. энергией, накопленной при колебаниях. Давайте усред­ним мощность по многим циклам, когда сила включена уже давно и осциллятор изрядно наколебался. Если пробег длится долго, запасенная энергия не изменяется; производная по вре­мени дает эффект, в среднем равный нулю. Иными словами, если усреднить затраченную за долгое время мощность, то вся энергия поглотится из-за сопротивления, описываемого членом gm(dx/dt)². Определенную часть энергии осциллятор, конечно, запасет, но если усреднять по многим циклам, то количество ее не будет меняться со временем. Таким
образом, средняя мощ­ность <P> равна

Применяя метод комплексных чисел и нашу теорему о том, что <А²>=¹/₂A²₀, легко найти эту среднюю мощность. Так как

, то . Следовательно, средняя мощность равна

<P>=¹/₂gw²x²₀. (24.4)

Если перейти к электрическим цепям, то dx/dt надо заменить на ток I (I — это dq/dt, где q соответствует х), а gm — на сопро­тивление R. Значит, скорость потери энергии (мощности силы) в электрической цепи равна произведению сопротивления на средний квадрат силы тока

<Р>=R<I²>=R^l/₂I²₀. (24.5)

Энергия, естественно, переходит в тепло, выделяемое сопро­тивлением; это так называемые тепловые потери, или джоулево тепло.

Интересно разобраться также в том, много ли энергии может накопить осциллятор. Не путайте этого вопроса с вопросом о средней мощности, ибо хотя выделяемая силой мощность сна­чала действительно накапливается осциллятором, потом на его долю остается лишь то, что не поглотило трение. В каждый мо­мент осциллятор обладает вполне определенной энергией, по­этому можно вычислить среднюю запасенную энергию <E>. Мы уже вычислили среднее значение (dx/dt)², так что

Если осциллятор достаточно добротен и частота w близка к w₀, то ½х½ — большая величина, запасенная энергия очень велика и можно накопить очень много энергии за счет небольшой силы. Сила производит большую работу, заставляя осциллятор рас­качиваться, но после того, как установилось равновесие, вся сила уходит на борьбу с трением. Осциллятор располагает большой энергией, если трение очень мало, и потери энергии невелики даже при очень большом размахе колебаний. Доб­ротность осциллятора можно измерять величиной запасенной энергии по сравнению с работой, совершенной силой за период колебания.

Что это за величина — накопленная энергия по сравнению с работой силы за цикл? Ее обозначили буквой Q.Величина Q — это умноженное на 2p отношение средней запасенной энер­гии к работе силы за один цикл (можно рассматривать работу не за цикл, а за радиан, тогда в определении Q исчезнет 2p)

Пока Q не слишком велика — это плохая характеристика системы, если же Q довольно большая величина, то можно сказать, что это мера добротности осциллятора. Многие пыта­лись дать самое простое и полезное определение Q; разные оп­ределения немногим отличаются друг от друга, но если Q очень велика, то все они согласуются друг с другом. При самом общем определении по формуле (24.7) Q зависит от w. Если мы имеем дело с хорошим осциллятором вблизи резонансной частоты, то (24.7) можно упростить, положив w = w₀, тогдаQ=w₀/g, такое определение Q было дано в предыдущей главе. Что такое Q для электрической цепи? Чтобы найти эту ве­личину, надо заменить m на L, mg на R и mw²₀ на 1/С (см. табл. 23.1). Тогда q в точке резонанса равна Lw/R, где w — ре­зонансная частота. В цепи с большой Q запасенная цепью энергия велика по сравнению с работой за один цикл, произ­водимой поддерживающей колебания в цепи машиной.