Закон больших чисел и центральная предельная теорема
Если для неотрицательной случайной величины  существует математическое ожидание
существует математическое ожидание  , то для всех
, то для всех 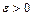 выполняется неравенство:
выполняется неравенство:
 (первое неравенство Чебышева).
(первое неравенство Чебышева).
Если для случайной величины  существует дисперсия
существует дисперсия  , то для всех
, то для всех 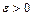 выполняется второе неравенство Чебышева:
выполняется второе неравенство Чебышева:
1)  (в центрированной форме);
(в центрированной форме);
2)  (в нецентрированной форме).
(в нецентрированной форме).
Второе неравенство Чебышева часто используют в виде:
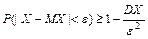 ,
, 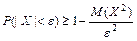 .
.
Последовательность случайных величин 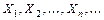 называют сходящейся по вероятности к случайной величине
называют сходящейся по вероятности к случайной величине  (кратко записывается
(кратко записывается  ), если для всех
), если для всех  :
: 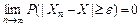 .
.
Говорят, что для последовательности случайных величин 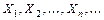 , имеющих математические ожидания
, имеющих математические ожидания  ,
, 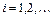 , выполняется закон больших чисел, если
, выполняется закон больших чисел, если 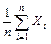

 , т.е. для всех
, т.е. для всех 
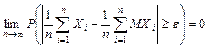 .
.
Закон больших чисел в форме Чебышева. Если последовательность независимых случайных величин 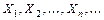 такова, что существуют
такова, что существуют  и
и 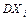 , причём дисперсии этих величин равномерно ограничены (не превышают постоянного числа
, причём дисперсии этих величин равномерно ограничены (не превышают постоянного числа  ), то для неё выполняется закон больших чисел, т.е.
), то для неё выполняется закон больших чисел, т.е. 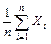

 . В частности, если случайные величины
. В частности, если случайные величины  ,
, 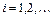 являются также одинаково распределёнными (в этом случае
являются также одинаково распределёнными (в этом случае  ,
,  ), то
), то 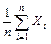

 .
.
Закон больших чисел в форме Бернулли. Если 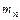 - число успехов в
- число успехов в  испытаниях по схеме Бернулли с вероятностью успеха
испытаниях по схеме Бернулли с вероятностью успеха  в отдельном испытании, то
в отдельном испытании, то 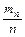

 , т.е. для всех
, т.е. для всех 
 .
.
Закон больших чисел в форме Бернулли является частным случаем закона больших чисел в форме Чебышева.
Центральная предельная теорема. Пусть 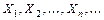 - последовательность независимых одинаково распределённых случайных величин (
- последовательность независимых одинаково распределённых случайных величин (  ,
,  ,
, 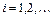 ), тогда последовательность нормированных случайных величин
), тогда последовательность нормированных случайных величин  , где
, где 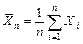 , сходится по распределению при
, сходится по распределению при  к стандартной нормальной величине
к стандартной нормальной величине  ~
~  , т.е. для всех
, т.е. для всех  :
: 
 .
.
12.236Средний срок службы мотора 4 года. Оценить снизу вероятность того, что данный мотор прослужит менее 20 лет.
12.237Среднее число вызовов, поступающих на станцию скорой помощи в течение часа, равно 30. Оценить вероятности, что в течение следующего часа число вызовов: а) превысит 40; б) будет не более 50.
12.238Известно, что  . В каких пределах находится
. В каких пределах находится  , если
, если  - неотрицательная случайная величина?
- неотрицательная случайная величина?
12.239Неотрицательные случайные величины  и
и  независимы. Оценить снизу вероятности событий:
независимы. Оценить снизу вероятности событий:  и
и  , если
, если  ,
,  .
.
12.240Пусть случайная величина  - число выпадений герба при 10 подбрасываниях монеты, а случайная величина
- число выпадений герба при 10 подбрасываниях монеты, а случайная величина  - число выпавших очков при одном бросании игральной кости. Оценить снизу вероятность события
- число выпавших очков при одном бросании игральной кости. Оценить снизу вероятность события  .
.
12.241Оценить снизу вероятность того, что отклонение любой случайной величины от её математического ожидания по абсолютной величине будет не более трёх средних квадратичных отклонений (правило трёх сигм).
12.242Случайная величина  имеет числовые характеристики
имеет числовые характеристики  ,
,  . Оценить снизу вероятности следующих событий:
. Оценить снизу вероятности следующих событий:
а)  ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
12.243Известно, что  . В каких пределах находится среднее квадратичное отклонение
. В каких пределах находится среднее квадратичное отклонение  случайной величины
случайной величины  ?
?
12.244Устройство состоит из 10 независимо работающих элементов. Вероятность отказа каждого элемента за время  равна 0.05. Оценить вероятность того, что абсолютная величина разности между числом отказавших элементов и средним числом (математическим ожиданием) отказов за время
равна 0.05. Оценить вероятность того, что абсолютная величина разности между числом отказавших элементов и средним числом (математическим ожиданием) отказов за время  окажется: а) меньше двух; б) не меньше двух.
окажется: а) меньше двух; б) не меньше двух.
12.245Вероятность появления события 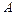 в каждом испытании равна 0.5. Оценить снизу вероятность того, что число
в каждом испытании равна 0.5. Оценить снизу вероятность того, что число  появлений события
появлений события 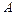 будет заключено в пределах от 40 до 60, если будет произведено 100 независимых испытаний.
будет заключено в пределах от 40 до 60, если будет произведено 100 независимых испытаний.
12.246Дискретная случайная величина  задана рядом распределения
задана рядом распределения 
 . Оценить вероятность того, что
. Оценить вероятность того, что  .
.
12.247Вероятность выхода со станка-автомата стандартной детали равна 0.96. Требуется: а) оценить снизу, используя неравенство Чебышева, вероятность того, что число бракованных среди 2000 деталей находится в пределах от 60 до 100 (включительно); б) уточнить вероятность того же, используя приближённую формулу Муавра-Лапласа.
12.248Для некоторого автопарка среднее число автобусов, отправляемых в ремонт после месяца эксплуатации на городских линиях равно 5. Оценить вероятность того, что по истечении месяца в данном автопарке в ремонт будет отправлено меньше 15 автобусов, если: а) отсутствует информация о дисперсии; б) известно, что дисперсия равна 4.
12.249Измеряется скорость ветра (  ) в данном пункте Земли. Случайная величина
) в данном пункте Земли. Случайная величина  - проекция вектора скорости на фиксированное направление. Оценить сверху вероятность события
- проекция вектора скорости на фиксированное направление. Оценить сверху вероятность события  при наличии следующей информации: а) путём многолетних измерений установлено, что
при наличии следующей информации: а) путём многолетних измерений установлено, что  ; б) в результате дополнительных измерений установлено, что
; б) в результате дополнительных измерений установлено, что  ; в) кроме информации, что
; в) кроме информации, что  и
и  известно также, что закон распределения случайной величины
известно также, что закон распределения случайной величины  симметричен относительно её математического ожидания.
симметричен относительно её математического ожидания.
12.250Последовательность независимых случайных величин  ,
,  задана указанным законом распределения. Выяснить применим ли к ней закон больших чисел в форме Чебышева, если:
задана указанным законом распределения. Выяснить применим ли к ней закон больших чисел в форме Чебышева, если:
а)  :
:  б)
б)  :
: 
12.251Для определения средней продолжительности горения электроламп в партии из 200 одинаковых ящиков было выбрано по одной лампе из каждого ящика. Используя закон больших чисел в форме Чебышева, оценить снизу вероятность того, что средняя продолжительность горения отобранных 200 электроламп отличается от средней продолжительности горения во всей партии по абсолютной величине меньше, чем на 5 часов, если известно, что среднее квадратичное отклонение продолжительности горения ламп в каждом ящике меньше 7 часов.
12.252Определить, используя закон больших чисел в форме Чебышева, сколько надо сделать замеров диаметров деревьев, чтобы средний диаметр деревьев на данном участке отличался от истинного значения диаметра не более чем на 2см с вероятностью не меньшей 0.95. Известно, что на данном участке среднее квадратичное отклонение диаметров деревьев не превышает 10 см.
12.253Вероятность наличия зазубрины на металлических брусках, заготовленных для обточки, равна 0.2. Используя закон больших чисел в форме Бернулли, оценить снизу вероятность того, что в партии из 1000 брусков отклонение относительной частоты появления бракованного бруска от вероятности его появления в отдельном испытании не превышает 0.05.
12.254Опыт страховой компании показывает, что на каждый пятый договор приходится страховой случай. Определить, используя закон больших чисел в форме Бернулли, сколько договоров надо заключить, чтобы с вероятностью 0.95 можно было утверждать, что доля страховых случаев отклонится от 0.2 не более чем на 0.05.
12.255Производится выборочное обследование большой партии электрических лампочек для определения среднего времени их горения. Среднее квадратичное отклонение времени горения лампочки равно  . Из всей партии наудачу выбирается 400 лампочек. Используя центральную предельную теорему, оценить вероятность того, что среднее время (математическое ожидание) горения лампочки будет отличаться от наблюденного среднего времени горения выбранных 400 лампочек не более чем на
. Из всей партии наудачу выбирается 400 лампочек. Используя центральную предельную теорему, оценить вероятность того, что среднее время (математическое ожидание) горения лампочки будет отличаться от наблюденного среднего времени горения выбранных 400 лампочек не более чем на  .
.