Составить программу, которая определяет, принадлежит ли точка с координатами (х , у) заштрихованной области. Координаты точки ввести с клавиатуры.
                8.1) у
-1 0
1 х
-1
|  8.16) у
-2 2
х
-2
| ||||||
 8.2) y
-2 2
x
-2
|  8.17)
| ||||||
 8.3) у
х
у=-х у=х
| 8.18)
 у
-1
0 1 х
-1
| ||||||
8.4) у
-1 0 1 х
-1 | 8.19)
У
 
 1
   -1
х
| ||||||
8.5)
 у
-1 1
0 х
| 8.20)
| ||||||
    8.6)
| 8.21)
у
-1 1 х
-1
| ||||||
8.7)
 у
0 1 х
-1
-1
| 8.22)
 у
-2 2
х
-2
| ||||||
8.8)
у
 1
-1
1 х
-1
| 8.23)
 у
-1 1 х
| ||||||
8.9)
у
0 х
-1 | 8.24)
 у
1 y=sinx
х
0 
| ||||||
8.10)
|  8.25)
у
-1 1
0 х
| ||||||
 8.11) у
R
У0
х
х0
|  8.26)
| ||||||
8.12)
| 8.27)
| ||||||
8.13)
у
-1 0 1 х
-1 | 8.28)
 у
-1 х
-2
| ||||||
8.14)
у
-1 1 2 х
-2 |               8.29) у
 1
-2
-1 1 х
-1 2
-2
| ||||||
 8.15)
у
х
  0 
| 8.30)
|
9. Составить программу для вычисления таблицы значений функций f (x) для x 
[a, b] с заданным шагом изменения x
| № п/п | f (x) | a | b | шаг |
| 0,1 | |||
| 0,1 | |||
| 0,2 | |||
| 0,2 | |||
| -5 | -1 | 0,4 | |
| -5 | -1 | 0,4 | |
| 0,2 | |||
| 0,2 | |||
| 0,1 | |||
| 0,1 | |||
| 0,1 | |||
| 0,1 | |||
| 0,2 | |||
| 0,2 | |||
| 0,05 | |||
| 0,05 | |||
| 0,2 | |||
| 0,2 | |||
| 0,1 | |||
| 0,1 | |||
| 0,05 | |||
| 0,05 | |||
| 0,5 | |||
| 0,5 | |||
| -3 | 0,1 | ||
| -3 | 0,1 | ||
| 0,2 | |||
| 0,2 | |||
| 0,1 | |||
| 0,1 |
10. Составить программу для вычисления элементов вектора х по формуле
10. 1) хi = ln |xi-1| + 
, i = 3,4,…,n
10. 2) хi = sin3xi-1 + 
, i = 3,4,…,m
10. 3) хi = ln 
- ln2 |ci-2|, i = 3,4,…,n
10. 4) xj = 
+ 
+ 
, j = 3,4,…,m
10. 5) xk = 
+ sin2 xk-1, k = 3,4,...,12
10. 6) хi = i · xi-1 + ln |xi-1| -1, i = 2,3,..., k
10. 7) xj = sin 
+ 
, j = 3,4,…,n
10. 8) хi = 
+ 
, i = 2,3,...,20
10. 9) xk = 
- ln |xk-1|, k = 2,3,...,m
10. 10) xj = cos2 xj-1 – tg x j-1, j = 2,3,…,15
10. 11) хi = 
+ 3 ln |xi-1|, i = 2,3,...,n
10. 12) xk = tg(xk-1-xk-2)+ 
, k = 3,4,...,10
10. 13) xj = 
+ 
+ 
, j = 4,5,…,m
10. 14) xk = sin3 xk/-1 + cos x 
+ 
, k = 3,4,...,15
10. 15) xk = cos x - ln |xk-1|, k = 2,3,...,n
10. 16) xj = cos xj-1+ sin2 xj-2+ 
, j = 4,5,…,20
10. 17) хi = 
, i = 2,3,...,n
10. 18) xk = ex 
+ sin2xk-1, k = 3,4,...,m
10. 19) xk = sin2 xk-1+ 
, k = 3,4,...,n
10. 20) xj = 
+sin3xj-1, j = 2,3,…,15
10. 21) хi = sin xi-4 · cos xi-2, i = 3,4,...,n
10. 22) xk = (k-1) · sin k · xk-1 + (k-2) · sin xk-2, k = 3,4,...,20
10. 23) хi = cos xi-1 + cos xi-2, i = 3,4,...,m
10. 24) xj = cos2 xj-1+ 
, j = 2,3,…,n
10. 25) xk = xk-1 + sin xk-2 + 
, k = 4,5,...,15
10. 26) хi = xi-1 · sin xi-2, i = 3,4,...,m
10. 27) xk = e-sin x 
+k · e-cos x 
, k = 3,4,...,n
10. 28) xj = cos e-x 
+ sin xj-1, j = 2,3,…,20
10. 29) хi = sin 
+ cos 
, i = 3,4,...,m
10. 30) xk = cos2 xk-2+ cos xk-1 + xk-3, k = 4,5,...,n.
11. Составить программу для вычисления суммы
| № | Выражение | № | Выражение |
| 
| ||
| 
| ||
|  , i = 2,4,6....,16
| ||
| 
| ||
 ,k= 2,4,6,...,20
|  , i = 1,3,5,...19
| ||
| 
| ||
|  , k = 3,5,...,15
| ||
| 
| ||
| 
| ||
| 
| ||
 ,k= 2,4,6,...,20
| 
| ||
|  , k = 3,5,7,...,17
| ||
|  , i = 3,5,...15
| ||
|  , i = 2,5,8,...,20
| ||
| 
|
12. Составить программу для вычисления произведения
| № п/п | Выражение | № п/п | Выражение |
| 
| ||
|  ,i= 2,4,6,...,16
| ||
 ,i= 2,4,6,...,20
| 
| ||
| 
| ||
 , i = 3,6,9,...,21
|  , i = 3,5,7,...,17
| ||
 ,i= 2,4,6,...,20
| 
| ||
|  , i = 3,6,9,...,15
| ||
 , i = 1,3,5,...,15
|  ,i= 3,5,7,...,17
| ||
| 
| ||
 , k = 1,3,5,...,15
| 
| ||
 , i = 2,4,...,16
|  , i = 3,5,7,...,15
| ||
| 
| ||
| 
| ||
 ,k=2,6,10,...,22
|  , j = 1,3,5,...,15
| ||
| 
|
13. Составить программу для вычисления величины S по формуле
| № п/п | Выражение | № п/п | Выражение |
S = 
| S = 
| ||
S = sin 
| S =  + 
| ||
S = 
| S = 
| ||
S = 
| S = 
| ||
S = 5 
| S =  +1
| ||
S =  +e 
| S = 
| ||
S = ln 
| S = 
| ||
S = 2· 
| S = 
| ||
S = e  + e 
| S = 
| ||
S = ln 
| S = 
| ||
S = 
| S =1-e 
| ||
S =1+e 
| S = 
| ||
S = 
| S =e  +e 
| ||
S = 
| S =  +ln 
| ||
S = 
| S = 
|
14. Составить программу для вычисления элементов матрицы Y по известным элементам вектора X.
| № п/п | Выражение | № п/п | Выражение |
yi j = ln 
i, j = 1,2,...,10
| yi j = 
i, j = 1,2,...,k
| ||
| yi j = xi ·sin(i·xj) i, j = 1,2,...,n | yi j =  , если xi › 0 и xj › 0;
yij =  в противном случае
| ||
yi j = 
i, j = 1,2,...,15
| yi j =  , если xi › xj;
yi j =  в противном случае
| ||
yi j = 
i, j = 1,2,...,m
| yi j =  , если xi или xj › 1;
yij=  в противном случае
| ||
yi j = 
i, j = 1,2,...,20
| yi j =  , если sin xi › sin xj;
yi j =  в противном случае
| ||
yi j = e  ·sin xj
i, j = 1,2,...,k
| yi j =  , если xj ≠ 0 и xi › 0;
yij =  в противном случае
| ||
yi j = 
i, j = 1,2,...,10
| yi j =  , если xi › xj;
yij=  в противном случае
| ||
yi j = 
i, j = 1,2,...,m
| yi j =  , если xi › 1 и xj › 5;
yi j =  в противном случае
| ||
yi j = 
i, j = 1,2,...,15
| yi j =  , если xi › 0 и |xj| › 1,5;
yij =  в противном случае
| ||
yi j = 
i, j = 1,2,...,n
| yi j =  ,если i ‹ j или xi · xj › 0;
yij =  в противном случае
| ||
yi j = 
i, j = 1,2,...,20
| yi j =  , если xi ≠ 0 и xj ≠ 0;
yij = 1 в противном случае
| ||
yi j = 
i, j = 1,2,...,m
| yi j =  , если i ‹ j;
yi j =  в противном случае
| ||
yi j = 
i, j = 1,2,...,25
| yi j =  , если xi › xj и cos xi › 0,5;
yij=  в противном случае
| ||
yi j = 
i, j = 1,2,...,l
| yi j =  , если i ‹ j или  › 2;
yij=  в противном случае
| ||
yi j = 
i , j = 1,2,...,30
| yi j =  , если sin xi ≤ sin xj;
yi j =  в противном случае
|
15. Составить программу для вычисления величины S по заданной формуле
| № п/п | Выражение | № п/п | Выражение |
S= 
| S=2 
| ||
S= 
| S= 
| ||
S= 
| S= 
| ||
S= 
| S= 
| ||
S= 
| S= 
| ||
S= 
| S=3,4·10-3· 
| ||
S= 
| S= 
| ||
S= 
| S= 
| ||
S= 2 
| S= 
| ||
S= 
| S= 
| ||
S= 
| S= 
| ||
S= 
| S= 
| ||
S=5,8·10-4· 
| S= 
| ||
S= 
| S= 
| ||
S= 
| S= 
|
16. Составить программу для вычисления элементов одномерного массива по заданной формуле
| № п/п | Выражение | № п/п | Выражение |
к = 1,2,…,10
| 
к = 1,2,…,10
| ||
к = 1,2,…,n
| 
к = 1,2,…,m
| ||
к = 1,2,…,20
| 
к = 1,2,…,m
| ||
к = 1,2,…,l
| 
к = 1,2,…,n
| ||
к = 1,2,…,15
| 
к = 1,2,…,10
| ||
к = 1,2,…,10
| 
к = 1,2,…,l
| ||
к = 1,2,…,n
| 
к = 1,2,…,20
| ||
к = 1,2,…,m
| 
к = 1,2,…,n
| ||
к = 1,2,…,n
| 
к = 1,2,…,20
| ||
к = 1,2,…,n
| 
к = 1,2,…,l
| ||
к = 1,2,…,n
| 
к = 1,2,…,10
| ||
к = 1,2,…,n
| 
к = 1,2,…,15
| ||
к = 1,2,…,l
| 
к = 1,2,…,m
| ||
к = 1,2,…,10
| 
к = 1,2,…,m
| ||
к = 1,2,…,m
| 
к = 1,2,…,n
|
17. Используя нестандартные функции, составить программы для расчета указанных величин.
| № п/п | Выражение | № п/п | Выражение |
 ,  ,где 
|    где 
| ||
 ,  , где  , 
|   где
 
| ||
 где 
|   где
 
| ||
 , где 
|   где 
| ||
  где  
|   где
 
| ||
  где 
|   где
 
| ||
  где
 
|   где
 
| ||
  где 
|    где
 
| ||
  , где 
|   где 
| ||
  
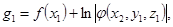где
 
|   где
 
| ||
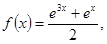
  где
 
|   где
 
| ||
  где 
|   где 
| ||
  где
 
|   где
 
| ||
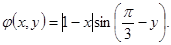
  где 
|   где
 
| ||
  где
 
|   где
 
|
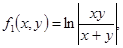
18. Написать подпрограмму
18.1) для замены в массиве Y(50) всех четных элементов на значение 1;
18.2) для замены знака каждого пятого элемента массива В(100) на противоположный;
18.3) для вычисления суммы отрицательных элементов массива А(200);
18.4) для расчета числа положительных элементов массива В(10,20);
18.5) для вычисления куба суммы положительных элементов массива Х(15,30);
18.6) для расчета суммы элементов второй строки матрицы Z(20,10);
18.7) для вычисления суммы элементов пятого столбца матрицы Z(10,20);
18.8) для отыскания минимального элемента массива Х(25);
18.9) для отыскания максимального элемента массива В(20,30) и индексов этого элемента;
18.10) для вычисления k!=1·2·3·…·k;
18.11) для замены в матрице А(10,10) всех элементов, стоящих на главной диагонали, на число 2;
18.12) для вычисления квадрата суммы элементов массива В(100), которые меньше 10;
18.13) для вычисления суммы положительных элементов 1-ой строки матрицы С(10,20);
18.14) для вычисления количества элементов матрицы В(30,30), которые лежат в интервале (2,5);
18.15) для расчета квадратного корня из суммы положительных элементов массива Х(m,n);
18.16) для вычисления минимального элемента 5-ой строки матрицы С (m,n) и номера столбца, в котором находится этот элемент;
18.17) для расчета количества нулевых элементов массива Х(k,n);
18.18) для замены знака всех нечетных элементов массива Z(150) на противоположный;
18.19) для вычисления следа (суммы элементов главной диагонали) матрицы В(m,m);
18.20) для замены знака на противоположный у всех элементов 5-го столбца матрицы А(m,n);
18.21) для вычисления максимального элемента матрицы Z(20,30) и определения номеров строки и столбца, которым принадлежит этот элемент;
18.22) для вычисления количества элементов массива Х(10,25), значения которых больше 10, и вычисления квадратного корня из суммы этих элементов;
18.23) для вычисления количества нулевых элементов 1-го столбца матрицы А(m,n);
18.24) для вычисления минимального элемента n-ой строки матрицы С(m,k);
18.25) для вычисления количества элементов массива Y(20,30), лежащих в интервале (0,2);
18.26) для расчета тангенса суммы положительных элементов массива Z(m,n);
18.27) для вычисления максимального и минимального элементов пятого столбца матрицы В(20,15) и определения номеров строк, в которых стоят эти элементы;
18.28) для замены всех элементов k-го столбца матрицы А(n,m) на число 1;
18.29) для расчета количества ненулевых элементов 1-ой строки матрицы В(k,m);
18.30) для нахождения количества положительных, отрицательных и нулевых элементов массива С(20,30).