Пример выполнения работы

 

1. Составить таблицу теоретического распределения ( 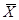=29,669; s=0,021).

 

xi min xi max fi mi [ 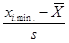; ) pi ni
29,63 29,641 0,12 -∞;-1,3333 0,0918 4,59
29,641 29,653 0,16 -1,3333;-0,7619 0,1318 6,59
29,653 29.664 0,14 -0,7619;-0,2381 0,1816 9,08
29.664 29.676 0,18 -0,2381;0,3333 0,2241 11,205
29.676 29.687 0,16 0,3333;0,8571 0,1758 8,79
29.687 29.699 0,12 0,8571;1,4286 0,1185 5,925
29.699 29.71 0,12 1,4286; ∞ 0,0764 3,82

 

 
 

Рис. 2. Теоретический полигон распределения и эмпирическая гистограмма

 

2. Нулевая гипотеза Н0: X ~ N( 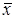,s2), т.е. совокупность имеет нормальное распределение, в качестве параметров которого взяты их наилучшие оценки.

Конкурирующая Н1: совокупность не имеет нормальное распределение.

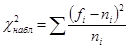=(6-4,59)2/4,59+(8-6,59)2/6,59+(7-9,08)2/9,08+
+(9-11,205)2/11,205+(8-8,79)2/8,79+(6-5,925)2/5,925+(6-3,82)2/3,82=2,96.

Степень свободы k=7-1-2=4.

Для a=0,01, k=4, < =11,3. Для a=0,05, k=4, < =9,5.

Вывод: наблюдаемое значение не превысило критические точки критерия Пирсона, следовательно, принимаем нулевую гипотезу Н0.

3. Составим таблицу накопленных частот

 

xi min xi max mi pi Gi=∑mi Fi=∑pi |Fi-Gi|
29,63 29,641 0,12 0,0918 0,12 0,0918 0,0282
29,641 29,653 0,16 0,1318 0,28 0,2236 0,0564
29,653 29.664 0,14 0,1816 0,42 0,4052 0,0148
29.664 29.676 0,18 0,2241 0,6 0,6293 0,0293
29.676 29.687 0,16 0,1758 0,76 0,8051 0,0451
29.687 29.699 0,12 0,1185 0,88 0,9236 0,0436
29.699 29.71 0,12 0,0764 1,0 1,0

 

Критерий Колмогорова 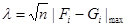=7,0711*0,0564=0,3988.

Ρ(λ)=0,9972>0,05.

Вывод: полученное значение вероятности превысило уровень значимости, следовательно, принимаем нулевую гипотезу Н0.

 

Значения вероятностей Ρ(λ) для различных λ

λ Ρ(λ) λ Ρ(λ) λ Ρ(λ) λ Ρ(λ)
0,30 1,000 0,70 0,7112 1,20 0,1122 1,90 0.0015
0,35 0,9997 0,75 0,6272 1,30 0,0681 2,00 0,0007
0,40 0,9972 0,80 0,5441 1,40 0,0397 2,10 0,0003
0,45 0,9874 0,85 0,4653 1,50 0,0222 2,20 0,0001
0,50 0,9639 0,90 0,3927 1,60 0,0120 2,30 0,0001
0,55 0,9228 0,95 0,3275 1,70 0,0062 2,40 0,0000
0,60 0,8643 1,00 0,2700 1,80 0,0032 2,50 0,0000
0,65 0,7920 1,10 0,1777        

 


РАСЧЕТНАЯ РАБОТА №5

 

ПРОВЕРКА СТАТИСТИЧЕСКИХ ГИПОТЕЗ

 

1. Проверить гипотезу о равенстве дисперсий нескольких генеральных совокупностей при уровне значимости a=0,05.

2. Проверить гипотезу о равенстве двух средних генеральных совокупностей при уровне значимости a=0,05.

3. Проверить гипотезы о равенстве выборочных средних гипотетической генеральной средней D при уровне значимости a=0,05.