Строгая аналогия
Характерным отличительным признаком строгой аналогии является наличие необходимой связи между сходными признаками и переносимым признаком. Схема строгой аналогии такая:
Предмет A обладает признаками a, b, с, d, e.
Предмет В обладает признаками a, b, с, d.
Из совокупности признаков а, b, с,d необходимо следует e.
Предмет B обязательно обладает признаком e.
Строгая аналогия применяется в научных исследованиях, в математических доказательствах. Например, формулировка признаков подобия треугольников основана на строгой аналогии: “Если три угла одного треугольника равны трем углам другого треугольника, то эти треугольники подобны” (подобие - вид аналогии).
На строгой аналогии основан метод моделирования. Известно, что единство природы обнаруживается в “поразительной аналогичности” дифференциальных уравнений, относящихся к
 |
разным областям явлений. В физике эти аналогичные явления весьма часты. Например, аналогичными уравнениями описываются корпускулярно-волновые свойства света и аналогичные свойства электронов. Закон Кулона, определяющий силу электростатического взаимодействия двух неподвижных друг относительно друга точечных зарядов q1 и q2,, расстояние между которыми r, выражается формулой:
Аналогичной формулой выражен закон всемирного тяготения Ньютона:
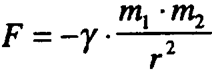 |
Здесь мы видим строгую аналогию, в которой переносимыми признаками являются не свойства, а отношения между разными объектами (электрическими зарядами и массами вещества), выраженные аналогичной структурой формул.
Строгая аналогия дает достоверный вывод, т. e. истину, обозначаемую в многозначных логиках, в классической логике, в теории вероятностей через 1. Вероятность вывода по строгой аналогии равна 1.