Аналіз міндеті-
Абсолюттік модель-
модель түсінгі матмеатикалық модель түсігінен шығып, желі туралы біліміне, барлығына қатысты болады.
Аналогтық модель-
Өзі нақты объект ретінде іс атқарады.
Аналіз міндеті-
Сыртқы орта сипаттамасы,жүйе құрылымы, жүйе сипаттамалары мен әрекетін зерттеу.
Ағаш тармақтары - бұл:
Ағашқа кірген графтың тармақтары.
Ағашқа кірмеген графтың тармақтары - бұл:
Хордалар.
Ағашқа кірген графтың тармақтары -бұл:
Ағаштың тармақтары.
Ағаш тармақтарының қимасы:
Қима сызығымен қиылысатын тармақтардың көпшілігі.
Ақпараттық-логикалық модель-
зерттелудегі объект қажетті ақпараттардың барлығын қамтиды.
Ақпараттық модель?
Бұл объектінің қандайда бір тілдегі сипаттамасы.
Альтернативті варьирлеу бір шамасының байқалу мүмкіндігі өте аз болса, ал екіншісінің бірлікке жақындаса, биноминальды таратылу анық көрінетін асимметрияға ие- бұл:
Пуассон таратылуы.
Әлемнің нақты объектілерін логикалық, математикалық көмегімен танылады-
Рациональдық принципі.
Барлық формалар біртіндеп төменгі формадан дамиды.Төменгі формалар күшін болжауға болады
Эволюция принципі.
Барлық тармақтары әр түрлі маршрут - бұл:
Тізбек.
Бастапқы графтан бірнеше тармақтарды алып тастау арқылы пайда болған графтың бөлігі:
Суграф.
Бастапқы графтан бірнеше түйіндер мен тармақтарды алып тастау арқылы пайда болған граф:
Графтың бөлігі.
Бірқалыпты үлестірім функциясы сипатталады-
F(x)=1/(b-a).
Бір түйінге қарайтын тармақтардың бірізділігі:
Маршрут.
Бір жүйенің әрбір элемнтіне басқа жүйенің әрбір төменгі сәйкестенетін өзара бірмәнді сәйкесі бар екі жүйені-
Изоморфты.
Бір кездейсоқ шаманың көмегімен есептелген параметрдің жақындатылған мәні - бұл:
Параметрдің бағалануы.
Беріктіктің сандық сипаттамасы сияқты дайындық коэффициентінің кемшілігі:
Оның шамасына қарап жүйенің тоқтаусыз жұмыс істеу уақыты туралы тұжырым жасауға мүмкіндік болмайды.
Вариация - бұл:
Өзгермеліктігі немесе әр түрлі кездейсоқ және кездейсоқ емес шамалардың әсерлерінен байқалатын қасиеттері.
Вариация коэффициенті - бұл:
Зерттелетін шаманың варьирлеудің салыстырмалы дәрежесінің сипаттамасы ретінде қабылданған көрсеткіш.
Виозиологиялық модель-
Табиғаттың объективті заңдарын оқып үйренуге бағытталған.
Графикалық модельдерге жататын топ
Сызбалар үлгісі.
Граф - бұл:
Түйіндердің және оларды байланыстыратын тармақтардың жиынтығы.
Графтың нақты ағашы - бұл:
Нақты бірізділікпен тармақтары қосылатын фундаментальды ағаш.
Графтың бөлігі- бұл:
Бастапқы графтан бірнеше түйіндер мен тармақтарды алып тастау арқылы пайда болған граф.
Графтың ағашы - бұл:
Циклы жоқ байланысқан подграф.
Геометриялық үлестірім деп-
Егер кейбір оқиға р ықтималдығымен орындалатын болса, онда осы оқиғаның пайда болуына дейінгі бірінен-бірі тәуелсіз сынақтардың кездейсоқ саны.
Графтың тармақтар көбейтінісінен және олар қарайтын түйіндерден пайда болған графтың бөлігі - бұл:
Подграф.
Графикалық тәсіл арқылы есептің шешімін табыныз: F=x1+x2
X1+2x2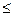 
14
-5x1+3x2 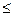15
Fmax=14; X1=14 ; X2=0.
Графикалық тәсіл арқылы есептің шешімін табыныз: F=x1+2x2
4x1-2x2 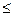12
-x1+3x2 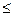6
2x1+4x2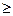 
16
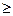X1 X2 0
Fmax=12; X1=4.8; X2=3.6.
Графикалық тәсіл арқылы есептің шешімін табыныз: F=-2x1+x2
3x1-2x2 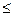12
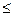-x1+3x2 8
2x1+2x2 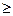8
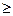X1 X2 0
Fmax=-11; X1=10; X2=9.
Графикалық тәсіл арқылы есептің шешімін табыныз:
F=-x1+4x+2x4-x5
3x1-2x2 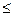12
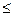-x1+3x2 8
2x1+2x2 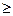8
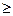X1 X2 0
Fmax=22; X+=(2,6,33,0,0) .
Графикалық тәсіл арқылы есептің шешімін табыныз:
F=-5x1+x2-x3
3x1-x2-x3=4
x1-x2+x3-x4=1
2x1+x2+2x3+x5=7
X1 X2 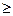0
Fmax=-20/3; X+=(4/3,0,0,13,13/3).
Графикалық тәсіл арқылы есептің шешімін табыныз:
F=x1+x2
2x+4x 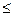16
-4x12x2 8
2x1+x2 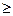9
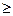X1 X2 0
Fmax=7; X1=6; X2=1.
Графикалық тәсіл арқылы есептің шешімін табыныз:
F=x1+x2
2x1 + x2 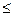16
-4x1+ x2 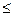18
x1+3x2 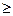9
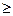X1 X2 0
Fmax=3; X1=0; X2=3.
Графикалық тәсіл арқылы есептің шешімін табыныз:
F=30x1+40x2
12x1+4x2 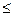300
4x1+4x2 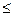120
3x1+12x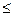2 252
X1 X2 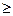0
Fmax=1080; X1=12; X2=18.