Закономерности распределения магнитных полей в скважине

Вектор напряженности аномального магнитного поля и его составляющие определяются из уравнений

 

,

,

(12.2)

X_a = ,

 

Y_a = .

На рис. 12.3 показано распределение кривых Xа, Zа, Та векторов Та вдоль линии, расположенной в стороне от штока. Экстремальные значения кривой Zа – над кромкой стержня (максимум) и ниже ее (минимум). Все векторы Та направлены в сторону намагниченной кромки штока. Годограф векторов Та – замкнутая кривая – лемниската.

Аналогичные закономерности можно выявить и для других элементарных магнитных источников.

1 2 3 4 5

 

Рис. 12.3. Магнитное поле в скважине от штока:

а – составляющие и векторы Т_а, б – годограф векторов Т_а;

1 – Н_а, 2 – Z_а, 3 - /Т_а/, 4 – векторы Т_а, 5 – годограф Т_а

 

Тонкий пласт, намагниченный по падению и имеющий большое распространение в глубину. Пусть тонкий пласт представлен в системе координат: ось у параллельна простиранию пласта, ось z совпадает с осью скважины (рис.12.3), тогда составляющие магнитного поля могут быть определены из уравнений

 

,

(12.3)

.

 

Модуль вектора Т_а будет равен Т_а :

 

,

где .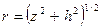

 

Рис. 12.4. Магнитное поле в скважине от пласта малой мощности

 

Местоположение верхней кромки пласта определяется сходящимся веером векторов Т_а, а нижней кромке тонкого пласта будет соответствовать расходящийся веер векторов.

При отклонении вектора намагниченности J от плоскости пласта на угол i уравнения (12.3) будут иметь вид

 

,

(12.4)

.

 

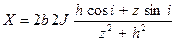Модуль вектора Т_а при прямой и косой намагниченности остается неизменным, он является только функцией расстояния от кромки пласта (рис.12.5). Вектор Т_а в случае вертикальной намагниченности будет перпендикулярен оси скважины в точках максимума кривой его модуля. При произвольной намагниченности вектор Т_а отклонится от перпендикуляра на угол i. Развернув весь веер на этот угол, можно определить истинное положение кромок тела.

а в

Рис. 12.5. Вектор Та и его модуль при прямом и произвольном векторе намагниченности:

а – намагниченность по оси падения пласта; в– произвольная намагниченность

 

Если нижняя граница пластообразного тела оказывает влияние на вид аномалии, то картина распределения магнитного поля будет намного сложнее. На рис.12.6 приведены теоретические кривые и векторные диаграммы для маломощного пласта, ограниченного по падению. Рассмотрены два пласта с вертикальной намагниченностью, но различного падения. Как видно из приведенных графиков и направлений векторов, пересечение полных векторов не совпадает с границами пласта. Расхождение тем больше, чем дальше от скважины расположен пласт.

Магнитное поле шара. Если магнитный источник сферической формы удален по перпендикуляру от ствола скважины на расстоянии

 

h = ( х² + у²)^1/2,

то при осевой схеме ориентации датчиков составляющие магнитного потенциала будут равны

 

 

Рис.12.6. Магнитное поле тонких пластов, ограниченных по падению:

а – вертикальное падение; в – наклонное падение

 

 

,

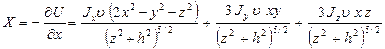(12.5)

.

 

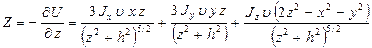В случае, если скважина проходит через центр сферы, то выражение (12.5) упрощается:

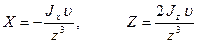–вне сферы;

(12.6)

– внутри сферы.

 

На рис. 12.7 приведены графики Zа и векторы Та для шара по вертикальным линиям наблюдения, расположенным вне сферы и внутри сферы. График Z_а центрального пересечения четко отражает размеры сферы и определяет ее местоположение. Графики Z_а краевого пересечения, расположенные вне сферы, могут дать информацию о стороне расположения магнитного источника.

 

 

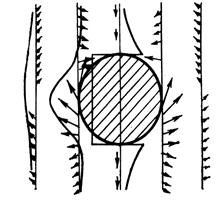
Рис.12.7. Кривые Z_а и векторы Т_а по вертикальной линии наблюдений для шара