МЕХАНИКА

 

1. Две автомашины движутся по дорогам, угол между которыми a=60°. Скорость автомашин 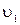=54 км/ч и 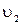=72 км/ч. С какой скоростью и удаляются машины одна от другой?

2. Материальная точка движется прямолинейно с начальной скоростью 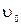=10 м/с и постоянным ускорением а=-5м/с². Определить, во сколько раз путь Ds, пройденный материальной точкой, будет превышать модуль ее перемещения Dr спустя t=4 с после начала отсчета времени.

3. Тело брошено горизонтально с начальной скоростью 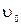=10 м/с. Через t=2 с после начала движения, пренебрегая сопротивлением воздуха, найти: а) угол между вектором скорости и вертикалью; б) модули тангенциального и нормального ускорений; в) радиус кривизны траектории в точке, соответствующей этому моменту времени.

4. Движение точки по окружности радиуса R=4 м задано уравнением s=A+Bt+Ct², где A=10 м, В=-2 м/с, С=1 м/с². Найти тангенциальное а_t, нормальное a_n и полное а ускорение точки в момент времени t=2с.

5. По дуге окружности радиуса R=10 м движется точка. В некоторый момент времени нормальное ускорение точки a_n=4,9 м/с²; вектор полного ускорения образует в этот момент с вектором нормального ускорения угол j=60⁰. Найти скорость 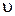и тангенциальное ускорение а_t точки.

6. Точка движется по окружности радиуса R=2 м согласно уравнению s=At³, где A=2м/с³. В какой момент времени t нормальное ускорение а_n точки будет равно тангенциальному а_t. Чему будет равно полное ускорение a в этот момент времени?

7. Движение точки по кривой задано уравнениями x=A₁t³, где A₁=l м/c³ и y=A₂t, где A₂=2 м/с. Найти уравнение траектории точки, ее скорость 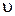и ускорение а в момент времени t=0,8 с.

8. Пистолетная пуля пробила два вертикально закрепленный листа бумаги, расстояние между которыми l=30 м. Пробоина во втором листе оказалась на h=10 см ниже, чем в первом. Определить скорость 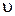пули, если к первому листу она подлетела, двигаясь горизонтально. Сопротивлением воздуха пренебречь.

9. Тело брошено под углом a=30° к горизонту со скоростью 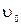=30 м/с. Каковы будут нормальное а_n и тангенциальное a_t ускорения тела через время t=1c после начала движения?

10. Тело брошено под некоторым углом a к горизонту. Найти величину этого угла, если горизонтальная дальность s полета тела в четыре раза больше максимальной высоты Н траектории.

11. Камень брошен с вышки в горизонтальном направлении со скоростью 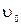=30 м/с. Определить скорость 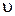, тангенциальное а_t и нормальное а_n ускорения камня в конце второй секунды после начала движения.

12. Тело брошено под углом a=30° к горизонту. Найти тангенциальное а_t и нормальное а_n ускорения в начальный момент движения.

13. Небольшое тело начинает движение по окружности радиусом R=30 м с постоянным по модулю тангенциальным ускорением а_t=5 м/с². Найти полное ускорение тела через t=3 с после начала движения.

14. Материальная точка движется по окружности радиусом R=5 м. Когда нормальное ускорение точки становится a_n=3,2 м/с, угол между векторами полного и нормального ускорений j=60°. Найти модули скорости и тангенциального ускорения точки для этого момента времени.

15. Нормальное ускорение частицы, движущейся по окружности радиусом R=3,2 м, изменяется по закону а=At², где А=2,5 м/с⁴. Найти: а) путь, пройденный частицей за t=5 с после начала движения; б) тангенциальное и полное ускорения в конце этого участка пути.

16. Автомобиль, движущийся со скоростью 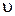=54 км/ч, проходит закругление шоссе радиусом кривизны R=375 м. На повороте шофер тормозит машину, сообщая ей ускорение а_t=0,5 м/с². Найти модули нормального и полного ускорений автомобиля на повороте и угол между их направлениями.

17. Точка движется по окружности так, что зависимость пути от времени описывается уравнением s=Bt+Ct², где В=-2 м/с, С=2 м/с². Через t₁=1 с после начала движения нормальное ускорение точки а_n=0,5 м/с². Найти время t, при котором модули нормального и тангенциального ускорения будут равны.

18. На цилиндр, который может вращаться около горизонтальной оси, намотана нить. К концу нити привязали грузик и предоставили ему возможность опускаться. Двигаясь равноускоренно, грузик за время t=3 с опустился на А=1,5 м. Определить угловое ускорение e цилиндра, если его радиус r=4 см.

19. Диск радиусом r=10 см, находившийся в состоянии покоя, начал вращаться с постоянным угловым ускорением e=0,5 рад/с². Каковы были тангенциальное а_t, нормальное а_n и полное а ускорения точек на окружности диска в конце второй секунды после начала вращения?

20. Диск радиусом r=20 см вращается согласно уравнению j=A+Вt+Сt³, где A=3 рад, B=-1 рад/с, С=0,1 рад/с³. Определить тангенциальное а_t, нормальное a_n и полное а ускорения точек на окружности диска для момента времени t=10 c.

21. На полу стоит тележка в виде длинной доски, снабженной легкими колесами. На одном конце доски стоит человек. Масса его m₁=60 кг, масса доски m₂=20 кг. С какой скоростью (относительно пола) будет двигаться тележка, если человек пойдет вдоль нее со скоростью (относительно доски) 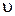=1 м/с? Массой колес и трением пренебречь.

22. На сколько переместится относительно берега лодка длиной l=3,5 м и массой m₁=200кг, если стоящий на корме человек массой m₂=80кг переместится на нос лодки? Считать лодку расположенной перпендикулярно берегу.

23. Лодка длиной l=3 м и массой m=120 кг стоит на спокойной воде. На носу и корме находятся два рыбака массами m₁= 60 кг и m₂=90 кг. На сколько сдвинется лодка относительно воды, если рыбаки поменяются местами?

24. В лодке массой m₁=240 кг стоит человек массой m₂=60 кг. Лодка плывет со скоростью 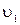=2 м/с. Человек прыгает с лодки в горизонтальном направлении со скоростью 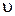=4 м/с (относительно лодки). Найти скорость движения лодки после прыжка человека: 1) вперед по движению лодки и 2) в сторону, противоположную движению лодки.

25. На полу стоит тележка в виде длинной доски, снабженной легкими колесами. На одном конце доски стоит человек. Масса человека М=60 кг, масса доски m=20 кг. С какой скоростью u (относительно пола) будет двигаться тележка, если человек пойдет вдоль доски со скоростью (относительно доски) 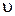=1 м/с? Массой колес пренебречь. Трение во втулках не учитывать.

26. На платформе установлена безоткатная пушка, из которой производится выстрел вдоль железнодорожного пути под углом 45° к горизонту. Определить начальную скорость снаряда, если известно, что после выстрела платформа откатилась на расстояние 3,0 м. Масса платформы с пушкой М=2,0∙10⁴ кг, масса снаряда m=10 кг, коэффициент трения качения между колесами платформы и рельсами m=0,002.

27. Граната брошена под углом 45° к горизонту со скоростью 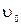=20 м/с. Через 2,0 с после момента бросания граната разрывается на два осколка, массы которых относятся как 1:2. Меньший осколок в результате взрыва получил дополнительную скорость 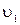=50 м/с, направленную горизонтально вдоль направления бросания гранаты. Определить дальность полета большего осколка, если известно, что меньший осколок упал на расстояние s₁=83 м. Сопротивление воздуха не учитывать.

28. Шар массой m₁=4 кг движется со скоростью 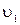=5 м/с и сталкивается с шаром массой m₂=6 кг, который движется ему навстречу со скоростью 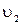=2 м/с. Определить скорости u₁ и u₂ шаров после удара. Удар считать абсолютно упругим, прямым, центральным.

29. Человек массой m₁=70 кг, бегущий со скоростью 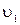=9 км/ч, догоняет тележку массой m₂=190 кг, движущуюся со скоростью 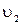=3,6 км/ч, и вскакивает на нее. С какой скоростью станет двигаться тележка с человеком? С какой скоростью будет двигаться тележка с человеком, если человек до прыжка бежал навстречу тележке?

30. Конькобежец, стоя на коньках на льду, бросает камень массой m₁=2,5 кг под углом a=30° к горизонту со скоростью 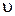=10 м/с. Какова будет начальная скорость 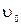движения конькобежца, если масса его m₂=60 кг? Перемещением конькобежца во время броска пренебречь.

31. Тяжелый шарик, подвешенный на легкой нерастяжимой нити длиной l=0,5 м, вращается в горизонтальной плоскости. Нить образует с вертикалью угол a=30°. Найти период вращения шарика.

32. Какое наибольшее ускорение может развить автомобиль при движении вверх по наклонной дороге с углом наклона a=20°, если коэффициент трения колес о покрытие дороги m=0,5? Какой путь пройдет автомобиль за t=10 с, если в момент начала подъема скорость его 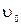=10 м/с?

33. На краю стола высоты h=1 м лежит маленький шарик массы M=200 г. В него попадает пуля массой m=10 г, летящая горизонтально со скоростью v=100 м/с, направленной в центр шарика. Пуля застревает в шарике. На каком расстоянии от стола по горизонтали шарик упадет на землю? Под каким углом к горизонту и с какой скоростью он упадет?

34. В деревянный шар массой m₁=8 кг, подвешенный на нити длиной l=1,8 м, попадает горизонтально летящая пуля массой m₂=4 г. С какой скоростью летела пуля, если нить с шаром и застрявшей в нем пулей отклонилась от вертикали на угол a=3°? Размером шара пренебречь. Удар пули считать прямым, центральным.

35. По небольшому куску мягкого железа, лежащему на наковальне массой m₁=300 кг, ударяет молот массой m₂=8 кг. Определить КПД h удара, если удар неупругий. Полезной считать энергию, затраченную на деформацию куска железа.

36. Из ствола автоматического пистолета вылетела пуля массой m₁=10 г со скоростью 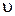=300 м/с. Затвор пистолета массой m₂=200 г прижимается к стволу пружиной, жесткость которой k=25 кН/м. На какое расстояние отойдет затвор после выстрела? Считать, что пистолет жестко закреплен.

37. Шар массой m₁=5 кг движется со скоростью 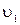=1 м/с и сталкивается с покоящимся шаром массой m₂=2 кг. Определить скорости u₁ и u₂ шаров после удара. Удар считать абсолютно упругим, прямым, центральным.

38. Из шахты глубиной h=600 м поднимают клеть массой m₁=3,0 т на канате, каждый метр которого имеет массу m=1,5 кг. Какая работа А совершается при поднятии клети на поверхность Земли? Каков коэффициент полезного действия h подъемного устройства?

39. Если на верхний конец вертикально расположенной спиральной пружины положить груз, то пружина сожмется на Dl=3 мм. На сколько сожмет пружину тот же груз, упавший на конец пружины с высоты h=8 см?

40. Из пружинного пистолета с пружиной жесткостью k=150 Н/м был произведен выстрел пулей массой m=8 г. Определить скорость и пули при вылете ее из пистолета, если пружина была сжата на Dх=4 см.

41. Цепь длиной l=2 м лежит на столе, одним концом свисая со стола. Если длина свешивающейся части превышает l/3, то цепь соскальзывает со стола. Определить скорость v цепи в момент ее отрыва от стола.

42. Какая работа А должна быть совершена при поднятии с земли материалов для постройки цилиндрической дымоходной трубы высотой h=40 м, наружным диаметром D=3,0 м и внутренним диаметром d=2,0 м? Плотность материала r принять равной 2,8∙10³ кг/м³.

43. Однородная цепь лежит на горизонтальной поверхности стола, и при этом один ее конец свисает со стола. Определить коэффициент трения, если известно, что цепь начинает соскальзывать со стола, когда длина свисающего конца составляет 1/6 часть общей длины цепи.

44. Молоток массой 0,80 кг в, момент удара о шляпку гвоздя имеет скорость 1,5 м/с и забивает его в бревно на глубину 5,0 мм. Какой массы груз необходимо положить на шляпку гвоздя, чтобы он вошел в бревно на такую же глубину?

45. Тело массой m=500 г, прикрепленное к резиновому шнуру длиной l₀=9,5 см, отклоняют на угол a=90° и отпускают. Коэффициент жесткости резинового шнура k=9,8 Н/см. Найти длину l резинового шнура в момент прохождения телом положения равновесия.

46. Груз, положенный на чашку весов, сжимает пружину на х₁=5 см. Найти величину сжатия пружины для случая, когда этот же груз падает на чашку весов с высоты h=10 см.

47. С какой наименьшей высоты h должен начать скатываться акробат на велосипеде (не работая ногами), чтобы проехать по дороже, имеющей форму «мертвой петли», радиусом r=4 м и не оторваться от дорожки в верхней точке петли? Трением пренебречь.

48. В баллистический маятник массой М=5 кг попала пуля массой m=10 г и застряла в нем. Найти скорость 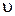пули, если маятник, отклонившись после удара, поднялся на высоту h=10см.

49. Два груза массами m₁=10 кг и m₂=15 кг подвешены на нитях длиною l=2 м так, что грузы соприкасаются между собой. Меньший груз был отклонен на угол j=60° и выпущен. На какую высоту h поднимутся оба груза после удара? Удар грузов считать неупругим.

50. Снаряд выпущен из орудия вертикально вверх с начальной скоростью v₀=200м/с. Считая силу сопротивления воздуха пропорциональной скорости, определите время подъема. Отношение коэффициента сопротивления к массе снаряда равно 0,02 с^-1.

51. По горизонтальной плоскости катится диск со скоростью 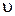=8 м/с. Определить коэффициент сопротивления, если диск, будучи предоставленным самому себе, остановился, пройдя путь s=18 м.

52. Блок, имеющий форму диска массой m=0,4 кг, вращается под действием силы натяжения нити, к концам которой подвешены грузы массами m₁=0,3 кг и m₂=0,7 кг. Определить силы натяжения Т₁ и Т₂ нити по обе стороны блока.

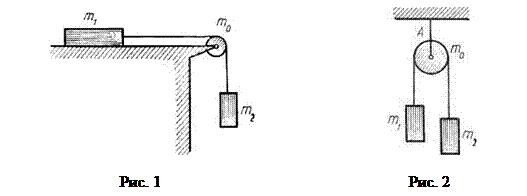
53. В системе, представленной на рис. 1, m₁=1 кг, m₂=1,2 кг, m₀=0,6 кг. Коэффициент трения между телом m₁ и горизонтальной поверхностью m=0,1. Блок m₀ считать однородным диском, скольжения нити по блоку нет, трением в оси блока пренебречь. В момент t=0 тело m₂ начинает опускаться. Найти работу силы трения, действующей на тело m₁ за первые t=3 с движения.

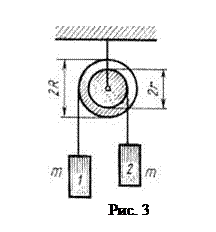
54. На рис. 2 m₁=600 г, m₂=450 г, m₀=600 г. Блок считать однородным диском, трением в оси пренебречь. Учитывая, что нить не скользит по блоку, найти: а) ускорения грузов m₁, m₂ , б) силы натяжения нитей; в) усилие F_A в подвеске.

 

55. На ступенчатый вал (рис. 3), радиусы которого R=0,2 м и r=0,1 м намотаны в противоположных направлениях нити, нагруженные одинаковыми массами m=1,0 кг. Момент инерции вала относительно его оси симметрии I=2∙10^-2 кг∙м². Массой нитей и трением в оси блока пренебречь. Найти ускорения грузов 1 и 2.

56. С одного уровня наклонной плоскости одновременно начинают скатываться сплошные цилиндр и шар одинаковых радиусов. Какое тело будет иметь большую скорость на данном уровне и во сколько раз? Во сколько раз скорость одного тела будет больше скорости другого в данный момент времени?

57. Однородные сплошные шар и цилиндр, имеющие одинаковый радиус, двигаясь с одинаковой скоростью по горизонтальной плоскости, вкатываются вверх по наклонной плоскости. Найти отношение высот подъема этих тел.

58. Однородный стержень длиной l=60 см может свободно вращаться вокруг горизонтальной оси, проходящей через один из его концов. Стержень отклонили от положения равновесия на угол a=15º и отпустили. Какую скорость будут иметь нижняя точка стержня и его центр масс при прохождении стержнем положения равновесия? Как изменится эти скорости, если угол отклонения увеличить в 6 раз?

59. Платформа в виде диска радиусом R=1 м вращается по инерции с частотой n=6 об/мин. На краю платформы стоит человек, масса которого m=80 кг. С какой частотой будет вращаться платформа, если человек перейдет в ее центр? Момент инерции платформы I=120 кг∙м². Момент инерции человека рассчитывать как для материальной точки.

60. При наличии трения обруч скатывается с наклонной плоскости, а при отсутствии скользит по ней. В каком случае и во сколько раз скорость, которую будет иметь обруч у основания наклонной плоскости, больше?

61. Однородный стержень длиной l=1,0 м может свободно вращаться вокруг горизонтальной оси, проходящей через один из его концов. В другой конец абсолютно неупруго ударяет пуля массой m=7 г, летящая перпендикулярно стержню и его оси. Определить массу М стержня, если в результате попадания пули он отклонится на угол a=60°. Принять скорость пули 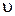=360 м/с.

62. Однородный стержень длиной l=1,0 м и массой М=0,7 кг подвешен на горизонтальной оси, проходящей через верхний конец стержня. В точку, отстоящую от оси на 2/3l, абсолютно упруго ударяет пуля массой m=5 кг, летящая перпендикулярно стержню и его оси. После удара стержень отклонился на угол a=60°. Определить скорость пули.

63. 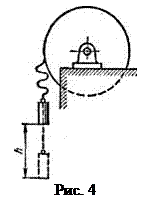Маховик, имеющий вид диска радиусом r=40 см и массой М=48 кг, может вращаться вокруг горизонтальной оси. К его цилиндрической поверхности прикреплен конец нерастяжимой нити, к другому концу которой подвешен груз массой m=0,2 кг (рис. 4). Груз был приподнят и затем отпущен. Упав свободно с высоты h=2 м, груз натянул нить и благодаря этому привел маховик во вращение. Какую угловую скорость w груз сообщил при этом маховику?

64. На краю горизонтальной платформы, имеющей форму диска радиусом r=2 м, стоит человек. Масса платформы M=200 кг, масса человека m=80 кг. Платформа может вращаться вокруг вертикальной оси, проходящей через ее центр. Пренебрегая трением, найти, с какой угловой скоростью w будет вращаться платформа, если человек будет идти вдоль ее края со скоростью u=2 м/с относительно платформы.

65. Шарик массой m=60 г, привязанный к концу нити длиной l₁=1,2 м, вращается с частотой n₁=2c^-1, опираясь на горизонтальную плоскость. Нить укорачивается, приближая шарик к оси до расстояния l₂=0,6 м. С какой частотой n₂ будет при этом вращаться шарик? Какую работу А совершает внешняя сила, укорачивая нить? Трением шарика о плоскость пренебречь.

66. Платформа, имеющая форму диска, может вращаться около вертикальной оси. На краю платформы стоит человек. На какой угол j повернется платформа, если человек пойдет вдоль края платформы и, обойдя его, вернется в исходную точку? Масса платформы M=240 кг, масса человека m=60 кг. Момент инерции I человека рассчитывать как для материальной точки.

67. На обод маховика диаметром D=60 см намотан шнур, к концу которого привязан груз массой m=2 кг. Определить момент инерции I маховика, если он, вращаясь равноускоренно под действием силы тяжести груза, за время t=3 с приобрел угловую скорость w=9 рад/с.

68. Нить с привязанными к ее концам грузами массами m₁=50 г и m₂=60 г перекинута через блок диаметром D=4 см. Определить момент инерции I блока, если под действием силы тяжести грузов он получил угловое ускорение e=1,5 рад/с². Трением и проскальзыванием нити по блоку пренебречь.

69. Стержень вращается вокруг оси, проходящей через его середину, согласно уравнению j=At+Bt³, где A=2 рад/с, В=0,2 рад/с³. Определить вращающий момент М, действующий на стержень через время t=2 с после начала вращения, если момент инерции стержня I=0,048 кг∙м².

70. Стержень вращается вокруг оси, проходящей через его конец, согласно уравнению j=Bt³, где В=0,1 рад/с³. Определить вращающий момент М, действующий на стержень через время t=2 с после начала вращения, если масса стержня m=400 г, а его длина l=1 м..

71. Материальная точка участвует в двух колебаниях, происходящих по одной прямой и выражаемых уравнениями x₁=3sint см; x₂=2cost см. Найти амплитуду A результирующего колебания, его частоту n и начальную фазу Dj.

72. Точка участвует одновременно в двух взаимно перпендикулярных колебаниях, выражаемых уравнениями x=2cost см; y=sint см. Определить траекторию точки и построить ее на чертеже. Показать направление движения точки.

73. Движение точки задано уравнениями x=10sin2t см; y=5sin(2t+1,57) см. Найти уравнение траектории и скорость точки в момент времени t=0,5 с.

74. Точка совершает гармонические колебания, уравнение которых имеет вид x=5sin2t см. В момент, когда возвращающая сила впервые достигла значения F=+5 мН, точка обладает потенциальной энергией П=100 мкДж. Найти этот момент времени t и соответствующую ему фазу колебаний j.

75. На концах тонкого стержня длиной l=30 см укреплены одинаковые грузики по одному на каждом конце. Стержень с грузиками колеблется около горизонтальной оси, проходящей через точку, удаленную на d=10 см от одного из концов стержня. Определить приведенную длину L и период T колебаний такого физического маятника. Массой стержня пренебречь.

76. Тонкий обруч, повешенный на гвоздь, вбитый горизонтально в стену, колеблется в плоскости, параллельной стене. Радиус обруча R=30 cм. Вычислить период колебаний.

77. Диск радиусом R=24 см колеблется около горизонтальной оси, проходящей через середину одного из радиусов перпендикулярно к плоскости диска. Определить приведенную длину L и период T колебаний такого маятника.

78. Из тонкого однородного диска радиусом R=20 см вырезана часть, имеющая вид круга радиусом r=10 см. Оставшаяся часть диска колеблется относительно горизонтальной оси О, совпадающей с одной из образующих цилиндрической поверхности диска. Найти период Т колебаний такого маятника.

79. Физический маятник в виде тонкого прямого стержня длиной l=120 см колеблется около горизонтальной оси, перпендикулярной к длине стержня и проходящей через точку, удаленную на некоторое расстояние a от центра тяжести стержня. При каком значении a период T колебаний имеет наименьшее значение?

80. Тело массой m=4 кг, закрепленное на горизонтальной оси, совершало колебания с периодом T₁=0,8 с. Когда на эту ось был насажен диск радиусом R=20 см и массой M=4 кг так, что геометрическая ось диска совпала с осью колебаний тела, период колебаний стал T₂=1,2 с. Найти момент инерции I тела относительно оси колебаний.

81. Амплитуда затухающих колебаний маятника за время t₁=5 мин уменьшилась в два раза. За какое время t₂, считая от начального момента, амплитуда уменьшится в восемь раз?

82. За время t=8 мин амплитуда затухающих колебаний маятника уменьшилась в три раза. Определить коэффициент затухания f.

83. Амплитуда A колебаний маятника длиной l=1 м за время t=10 мин уменьшилась в два раза. Определить логарифмический декремент затухания l.

84. Логарифмический декремент затухания колебаний маятника l=0,003. Сколько полных колебаний должен сделать маятник, чтобы амплитуда A уменьшилась в два раза?

85. Гиря массой m=500 г подвешена к спиральной пружине жесткостью k=20 Н/м и совершает упругие колебания в некоторой среде. Логарифмический декремент затухания l=0,004. Сколько колебаний должна совершить гиря, чтобы амплитуда A колебаний уменьшилась в два раза? За какое время t произойдет это уменьшение?

86. Тело массой m=5 г совершает затухающие колебания. В течение времени t=50 с тело потеряло 60% своей энергии. Определить коэффициент сопротивления.

87. Определить амплитуду А вынужденных колебаний груза массы т=0,1 кг на пружине с коэффициентом жесткости k=10 Н/м, если на груз действует вертикальная вынуждающая гармоническая сила с амплитудой Р=1,5 Н и частотой, в два раза большими собственной частоты груза на пружине. Коэффициент затухания m=0,4 с^-1.

88. Амплитуды смещений вынужденных колебаний при частотах вынуждающей силы 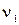=100 Гц и =150 Гц равны между собой. Найти частоту v, соответствующую резонансу смещений. Вынуждающая сила изменяется по гармоническому закону.

89. Тело массой т=0,1 кг совершает вынужденные прямолинейные колебания. Амплитудное значение вынуждающей силы F_y=1,5 Н. Коэффициент затухания m=0,5 с^-1. Определить максимальное значение амплитуды скорости.

90. Тело массой т=0,2 кг подвешено на невесомой пружине с коэффициентом жесткости k=50 Н/м. Под действием вынуждающей вертикальной силы с циклической частотой w=20 с^-1 тело совершает установившиеся вынужденные колебания с амплитудой A=20 мм. При этом смещение тела отстает по фазе от вынуждающей силы на 3p/4. Найти: а) логарифмический декремент затухания; б) работу вынуждающей силы за период колебаний.

91. Частица движется со скоростью 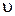=с/3, где с - скорость света в вакууме. Какую долю энергии покоя составляет кинетическая энергия частицы?

92. Протон с кинетической энергией Т=3 ГэВ при торможении потерял треть этой энергии. Определить, во сколько раз изменился релятивистский импульс a-частицы.

93. При какой скорости b (в долях скорости света) релятивистская масса любой частицы вещества в n=3раза больше массы покоя?

94. Определить отношение релятивистского импульса р-электрона с кинетической энергией Т=1,53 МэВ к комптоновскому импульсу m₀с электрона.

95. Скорость электрона 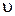=0,8с (где с - скорость света в вакууме). Зная энергию покоя электрона в мегаэлектрон-вольтах, определить в тех же единицах кинетическую энергию Т электрона.

96. Протон имеет импульс p=469 МэВ/с. Какую кинетическую энергию необходимо дополнительно сообщить протону, чтобы его релятивистский импульс возрос вдвое?

97. Во сколько раз релятивистская масса m_e элекрона, обладающего кинетической энергией Т=1,53 МэВ, больше массы покоя m₀?

98. Какую скорость b (в долях скорости света) нужно сообщить частице, чтобы ее кинетическая энергия была равна удвоенной энергии покоя?

99. Релятивистский электрон имел импульс p₁=m₀c. Определить конечный импульс этого электрона (в единицах m₀c.), если его энергия увеличилась в n=2 раза.

100. Релятивистский протон обладал кинетической энергией, равной энергии покоя. Определить, во сколько раз возрастет его кинетическая энергия, если его импульс увеличится в n=2 раза.

101. Частица движется со скоростью с/4, где с – скорость света в вакууме. Какую долю энергии покоя составляет кинетическая энергия частицы?

102. В системе K’ находится квадрат, сторона которого параллельна оси x’. Определить угол между его диагоналями в системе К, если система K’ движется относительно K со скоростью v=0,95 с.

103. Собственное время жизни мю-мезона равно 2 мкс. От точки рождения до точки распада в лабораторной системе отсчета мю-мезон пролетел расстояние l=6 км. С какой скоростью (в долях скорости света) двигался мезон?

104. Отношение заряда движущегося электрона к его массе, определенное из опыта, равно 0,88 10¹¹ Кл/кг. Определить релятивистскую массу электрона и его скорость.

105. На сколько процентов релятивистская масса частицы больше массы покоя при скорости v=30 Мм/с?

106. Известно, что объем воды в океане равен 1,37 10⁹ км³. Определить, на сколько возрастет масса воды в океане, если температура воды повысится на Dt=1ºС. Плотность воды в океане принять равной 1,03 10³ кг/м3.

107. на ракете, движущейся относительно Земли со скоростью vb, происходят две световые вспышки с промежутком времени между ними t₀=48с относительно корабля. Наблюдатель на Земле зафиксировал, что промежуток времени между вспышками равен t=80 с. С какой скоростью движется ракета?

108. На сколько изменится масса воды в океане за один год, если предположить, что поглощается 50% падающей на поверхность океана энергии излучения Солнца. Солнечная постоянная С (плотность потока энергии электромагнитного излучения Солнца на расстоянии, равном среднему расстоянию от Земли до Солнца) равна 1,4 кВт/м², принять площадь поверхности океана равной 3,6 10⁸ км².

109. Импульс релятивистской частицы равен m₀c. Под действием внешней силы импульс частицы увеличился в два раза. Во сколько раз возрастет при этом кинетическая энергия частицы, ее полная энергия?

110. Солнечная постоянная С (плотность потока энергии электромагнитного излучения Солнца на расстоянии, равном среднему расстоянию от Земли до Солнца) равна 1,4 кВт/м2. Определите, какую массу теряет Солнце в течение одного года?