Основные темы курса

Тема 1. Задачи эконометрики в области социально-экономических исследований. Основные этапы эконометрического моделирования.

Название «эконометрика», введенное норвежским экономистом и статистиком Рагнаром Фришем в буквальном переводе означает «измерения в экономике». Единое общепринятое определение эконометрики в настоящее время отсутствует, поэтому приведем высказывания известных ученых, дающие представление об этой науке.

Эконометрика – это раздел экономики, занимающийся разработкой и применением статистических методов для измерений взаимосвязей между экономическими переменными (Р.Фишер и др.)

Э.Маленво интерпретировал эконометрику как «любое приложение математики или статистических методов к изучению экономических явлений».

Эконометрика – самостоятельная экономико-математическая научная дисциплина, позволяющая на базе положений экономической теории и исходных данных экономической статистики, используя необходимый математико-статистический инструментарий, придавать конкретное количественное выражение общим (качественным) закономерностям, обусловленным экономической теорией (Айвазян С.А., Мхитарян В.С.).

Елисеева И.И. определяет эконометрику как науку, которая дает количественное выражение взаимосвязей экономических явлений и процессов.

Таким образом, эконометрика – это научная дисциплина, изучающая количественные стороны экономических явлений и процессов средствами математического и статистического анализа.

Эконометрика охватывает все аспекты применения математических методов в экономике, выявляет, строит и изучает конкретные количественные зависимости одних экономических показателей от других, используя статистические методы для обработки информации и оценки правдоподобия построений, а математические – для их анализа.

Главное назначение эконометрики – модельное описание конкретных количественных взаимосвязей, существующих между анализируемыми показателями.

Существует три основных класса эконометрических моделей:

Модели временных рядов, включающие модели:

- Тренда , где T(t) –временной тренд заданного параметрического вида, εi – случайная компонента;

- Сезонности 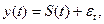где S(t) – периодическая (сезонная) компонента, εi – случайная компонента;

- Тренда и сезонности

аддитивная;

(мультипликативная);

Регрессионные модели с одним уравнением

В таких моделях зависимая переменная y представляется в виде функции , где - независимые (объясняющие) переменные. В зависимости от вида функции модели делятся на линейные и нелинейные.

Системы одновременных уравнений

Эти модели описываются системами одновременных уравнений, которые могут состоять из тождеств и регрессионных уравнений, каждое из которых может, кроме объясняющих переменных, включать в себя также объяснимые переменных из других уравнений системы.

Примером такой системы является модель спроса (Qd) и предложения (Qs), когда спрос на товар определяется его ценой (Р) и (I) потребителя, предложение – его ценой (Р) и достигается равновесие между спросом и предложением:

При эконометрическом моделировании мы встречаемся с двумя типами данных: пространственные данные (набор показателей экономических переменных в один и тот же момент времени) и временные ряды (серия наблюдений одной и той же случайной величины в последовательные моменты времени).

Весь процесс эконометрического моделирования можно разделить на шесть основных этапов:

- постановочный (на этом этапе формируется цель исследования, определяется набор участвующих в модели экономических переменных);

- априорный (проводится анализ экономической ущности изучаемого объекта, формирование и формализация известной до начала исследования (априорной) информации);

- параметризация (осуществляется непосредственно моделирование, т.е. выбор общего вида модели, в том числе состава переменных и формы их связи);

- информационный (собирается необходимая статистическая информация – наблюдаемые значения экономических переменных);

- идентификация модели (на этом этапе проводится статистический анализ модели и оценка ее параметров);

- верификация модели (проверяется истинность, адекватность модели, т.е. соответствие моделируемому реальному экономическому объекту).

На первых трех этапах весьма важной является проблема спецификации модели, включающая выражение в математической форме выявленных связей и соотношений, установление состава объясняющих переменных (в том числе и лаговых), формулировка исходных предпосылок и ограничений модели и ряд других вопросов. Спецификация опирается на имеющиеся экономические теории, специальные знания, а также на интуитивные представления об анализируемом экономическом объекте.

Широкому внедрению эконометрических методов способствовало развитие информационных технологий. Компьютерные эконометрические пакеты сделали эти методы более доступными. Наиболее трудоемкая работа по вычислению различных статистик, параметров, построению таблиц и графиков в основном выполняется компьютером, а исследователю остается работа по постановке задачи, выбору соответствующей модели и метода ее решения, а также интерпретации результатов.

Тема 2. Классическая и обобщенная линейные модели

множественной регрессии

 

Экономические явления определяются, как правило, большим числом совокупно действующих факторов. В связи с этим часто возникает задача исследования зависимости одной переменной Y от нескольких объясняющих переменных X1,Х2,…Хn. Эта задача решается с помощью множественного регрессионного анализа.

Построение уравнения множественной регрессии начинается с решения вопроса о спецификации модели, включающего отбор факторов и выбор вида уравнения регрессии. Факторы, включаемые во множественную регрессию, должны отвечать следующим требованиям:

- они должны быть количественно измеримы (качественным факторам необходимо придать количественную определенность);

- между факторами не должно быть высокой корреляционной, а тем более функциональной зависимости, т.е. наличия мультиколлинеарности.

Включение в модель мультиколлинеарных факторов может привести к следующим последствиям:

- Затрудняется интерпретация параметров множественной регрессии как характеристик действия факторов в «чистом виде», поскольку факторы связаны между собой; параметры линейной регрессии теряют экономический смысл;

- Оценки параметров ненадежны, имеют большие стандартные ошибки и меняются с изменением объема наблюдений.

Пусть - матрица – столбец значений зависимой переменной размера n;

- матрица значений, объясняющих переменных;

 

- матрица – столбец (вектор) параметров размера m+1;

- матрица – столбец (вектор) остатков размера n.

Тогда в матричной форме модель множественной линейной регрессии запишется следующим образом:

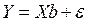(1)

При оценке параметров уравнения регрессии (вектора b) применяется метод наименьших квадратов (МНК). При этом делаются определенные предпосылки.

1. В модели (1) ε – случайный вектор, Х - неслучайная (детерминированная) матрица.

2. Математическое ожидание величины остатков равно нулю: М(ε) = 0n.

3. Дисперсия остатков εi постоянна для любого i (условие гомоскедастичности), остатки εi и εj при i≠j не коррелированны: .

4. ε – нормально распределенный случайный вектор, т.е. ε~N(0n;σ2 En).

5. r(X)=m+1<n. Столбцы матрицы Х должны быть линейно независимыми (ранг матрицы Х максимальный, а число наблюдений n превосходит ранг матрицы).

Модель (1), в которой зависимая переменная, остатки и объясняющие переменные удовлетворяют предпосылкам 1-5 называется классической нормальной линейной моделью множественной регрессии (КНЛММР). Если не выполняется только предпосылка 4, то модель называется классической линейной моделью множественной регрессии (КЛММР).

Согласно методу наименьших квадратов неизвестные параметры выбираются таким образом, чтобы сумма квадратов отклонений фактических значений от значений, найденных по уравнению регрессии, была минимальной:

Решением этой задачи является вектор

Одной из наиболее эффективных оценок адекватности модели является коэффициент детерминации R2, определяемый формулой:

Коэффициент детерминации характеризует долю вариации зависимой переменной, обусловленной регрессией или изменчивостью объясняющих переменных. Чем ближе R2 к единице, тем лучше построенная регрессионная модель описывает зависимость между объясняющими и зависимой переменной.

Следует иметь в виду, что при включении в модель новой объясняющей переменной, коэффициент детерминации увеличивается, хотя это и не обязательно означает улучшение качества регрессионной модели. В этой связи лучше использовать скорректированный (поправленный) коэффициент детерминации R2, пересчитываемый по формуле:

где n – число наблюдений,

m – число параметров при переменных х.

Из формулы следует, что с включением в модель дополнительных переменных разница между значениями и увеличивается. Таким образом, скорректированный коэффициент детерминации может уменьшаться при добавлении в модель новой объясняющей переменной, не оказывающей существенного влияния на результативный признак.

Но использование только коэффициента детерминации для выбора наибольшего уравнения регрессии может оказаться недостаточным.

Средняя относительная ошибка аппроксимации рассчитывается по формуле:

Значимость уравнения регрессии в целом сводиться к проверке гипотезы об одновременном равенстве нулю всех коэффициентов регрессии при факторных признаках т.е. гипотезы:

Если данная гипотеза не отклоняется, то делается вывод о том, что совокупное влияние всех факторных признаков х1, х2, … хm , включенных в модель, на зависимую переменную y можно считать статистически несущественным. Проверка данной гипотезы осуществляется на основе дисперсионного анализа.

Основной идеей дисперсионного анализа является разложение общей суммы квадратов отклонений результативной переменной y от среднего значения y на «объясненную» и «остаточную»:

 

Для приведения дисперсий к сопоставимому виду, определяют дисперсии на одну степень свободы. Результаты вычислений заносят в специальную таблицу дисперсионного анализа.

 

 

Таблица 2.1.

Дисперсионный анализ

Компоненты дисперсии Сумма квадратов Число степеней свободы Оценка дисперсии на одну степень свободы
Общая m-1  
Объясненная m
Остаточная n-m-1

 

В данной таблице n – число наблюдений, m – число параметров при переменных х.

Сравнивая полученные оценки объясненной и остаточной дисперсии на одну степень свободы, определяют значение F – критерия Фишера, используемого для оценки значимости уравнения регрессии:

С помощью F – критерия проверяется нулевая гипотеза о равенстве дисперсий H0: SR2=S2.

Если нулевая гипотеза справедлива, то объясненная и остаточная дисперсии не отличаются друг от друга. Для того, чтобы уравнение регрессии было значимо в целом (гипотеза Н0 была опровергнута) необходимо, чтобы объясненная дисперсия превышала остаточную в несколько раз. Критическое значение F – критерия определяется по таблице Фишера – Снедекора.

Расчетное значение сравнивается с табличным, и если оно превышает табличное (Fрасч>Fтабл), то гипотеза Н0 отвергается, и уравнение регрессии признается значимым. Если Fрасч<Fтабл, то уравнение регрессии считается статистически незначимым. Нулевая гипотеза Но не может быть отклонена.

Расчетное значение F – критерия связано с коэффициентом детерминации R2 следующим соотношением:

где m –число параметров при переменных х;

n – число наблюдений.

Оценка значимости коэффициентов регрессии сводится к проверке гипотезы о равенстве нулю коэффициента регрессии при соответствующем факторном признаке, т.е. гипотезы:

Но : bi=0

Проверка гипотезы проводится с помощью t – критерия Стьюдента. Для этого расчетное значение t-критерия:

где bi – коэффициент регрессии при хi

mbi – средняя квадратическая ошибка коэффициента регрессии bi

сравнивается с табличным tтабл при заданном уровне значимости (для экономических процессов и явлений) и числе степеней свободы (n-2).

Если расчетное значение превышает табличное, то гипотезу о несущественности коэффициента регрессии можно отклонить.

Рассмотрим интерпретацию параметров модели линейной множественной регрессии. В линейной модели множественной регрессии коэффициенты регрессии bi характеризуют среднее изменение результата с изменением соответствующего фактора на единицу при неизменном значении других факторов, закрепленных на среднем уровне.

На практике часто бывает необходимо сравнить влияние на зависимую переменную различных объясняющих переменных, когда последние выражаются разными единицами измерения. В этом случае используют стандартизованные коэффициенты регрессии βi и коэффициенты эластичности Эi (i=1,2,…,m).

Уравнение регрессии в стандартизованной форме:

Где - стандартизованные переменных.

В результате такого нормирования средние значения всех стандартизованных переменных равны нулю, а дисперсии равны единице, т.е.

Коэффициенты «чистой» регрессии связаны со стандартизованными коэффициентами следующим соотношением:

Стандартизованные коэффициенты показывают, на сколько стандартных отклонений (сигм) изменится в среднем результат, если соответствующий фактор х1 изменится на одно стандартное отклонение (одну сигму) при неизменном среднем уровне других факторов. Сравнивая стандартизованные коэффициенты друг с другом, можно ранжировать факторы по силе их воздействия на результат.

Средние коэффициенты эластичности вычисляются по формуле:

Коэффициент эластичности показывает, на сколько процентов (от средней) изменится в среднем Y при увеличении только фактора Xi на 1%.

При эконометрическом моделировании реальных экономических процессов предпосылки КЛММР нередко оказываются нарушенными: дисперсии остатков модели не одинаковы (гетероскедастичность остатков), или наблюдается корреляция между остатками в разные моменты времени (автокоррелированные остатки). Тогда предпосылка «3» запишется следующим образом:

где Ώ – положительно определенная матрица.

Принимая, что дисперсия объясняющих переменных могут быть произвольными, мы получаем обобщенную линейную модель множественной регрессии (ОЛММР).

В этом случае оценка параметров модели осуществляется обобщенным методом наименьших квадратов (ОМНК):

Если модель гетероскедастична, то матрица Ώ – диагональная. Тогда имеем:

В этом случае обобщенный метод наименьших квадратов называется взвешенным методом наименьших квадратов, поскольку мы «взвешиваем» каждое наблюдение с помощью коэффициента 1/σi.

На практике, однако, значения σi почти никогда не бывают известны. Поэтому сначала находят оценку вектора параметров обычным методом наименьших квадратов. Затем находят регрессию квадратов остатков на квадратичные функции объясняющих переменных, т.о. уравнение

Где f(x) – квадратичная функция.

Далее по полученном уравнению рассчитывают теоретические значения и определяют набор весов Затем вводят новые переменных и находят уравнение . Полученная оценка и есть оценка взвешенного метода наименьших квадратов.

Проверить модель на гетероскедастичность можно с помощью следующих тестов: ранговой корреляции Спирмена; Голдфельда-Квандта; Уайта; Глейзера.

Рассмотрим тест на гетероскедастичность, применяемый в случае, если ошибки регрессии можно считать нормально распределенными случайными величинами, - тест Голдфельда-Квандта.

Все n наблюдений упорядочиваются в порядке возрастания значений фактора Х. затем выбираются m первых и m последних наблюдений.

Гипотеза о гомоскедастичности равносильна тому, что значения остатков e1,…,em и en-m+l,…,en представляют собой выборочные наблюдения нормально распределенных случайных величин, имеющих одинаковые дисперсии.

Гипотеза о равенстве дисперсий двух нормально распределенных совокупностей проверяется с помощью F – критерия Фишера.

Расчетное значение вычисляется по формуле (в числителе всегда большая сумма квадратов):

Гипотеза о равенстве дисперсий двух наборов по m наблюдений (т.е. гипотеза об отсутствии гетероскедастичности остатков) отвергается, если расчетное значение превышает табличное F>Fα;m-p;m-p, где p – число регрессоров.

Мощность теста (вероятность отвергнуть гипотезу об отсутствии гетероскедастичности, когда гетероскедастичности действительно нет) максимальна, если выбирать m порядка n/3.

Тест Голдфельда – Квандта позволяет выявить факт наличия гетероскедастичности, но не позволяет описать характер зависимостей дисперсий ошибок регрессии количественно.

Если прослеживается влияние результатов предыдущих наблюдений на результаты последующих, случайные величины (ошибки) εi в регрессионной модели не оказываются независимыми. Такие модели называются моделями с наличием автокорреляции.

Как правило, если автокорреляция присутствует, то наибольшее влияние на последующее наблюдение оказывает результат предыдущего наблюдения. Наличие автокорреляции между соседними уровнями ряда можно определить с помощью теста Дарбина-Уотсона. Расчетное значение определяется по следующей формуле:

Значения критерия находятся в интервале от 0 до 4. По таблицам критических точек распределения Дарбина-Уотсона для заданного уровня значимости , числа наблюдений (n) и количества объясняющих переменных (m) находят пороговые значения dн (нижняя граница) и dв (верхняя граница).

Если расчетное значение:

, то гипотеза об отсутствии автокорреляции не отвергается (принимается);

или , то вопрос об отвержении или принятии гипотезы остается открытым (расчетное значение попадает в зону неопределенности);

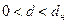, то принимается альтернативная гипотеза о наличии положительной автокорреляции;

, то принимается альтернативная гипотеза о наличии отрицательной автокорреляции.

 

Таблица 2.2.

Промежутки внутри интервала [0 - 4]

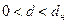
принимается альтернативная гипотеза о наличии положительнойавтокорреляции вопрос об отвержении или принятии гипотезы остается открытым (расчетное значение попадает в зону неопределенности) гипотеза об отсутствии автокорреляции не отвергается (принимается) вопрос об отвержении или принятии гипотезы остается открытым (расчетное значение попадает в зону неопределенности) принимается альтернативная гипотеза о наличии отрицательной автокорреляции

 

Недостаток теста Дарбина – Уотсона заключается прежде всего в том, что он содержит зоны неопределенности. Во-вторых, он позволяет выявить наличие автокорреляции только между соседними уровнями, тогда как автокорреляция может существовать и между более отдаленными наблюдениями. Поэтому наряду с тестом Дарбина-Уотсона для проверки наличия автокорреляции используются тест серий (Бреуша – Годфри),Q- тест Льюинга – Бокса и другие. Наиболее распространенным приемом устранения автокорреляции во временных рядах является построение авторегрессионных моделей.

 

Тема 3. Линейные регрессионные

модели с переменной структурой

 

При изучении социально-экономических процессов и явлений может оказаться необходимым включить в модель фактор, имеющий два или более качественных уровня, например, образование, пол, фактор сезонности. Качественные признаки могут существенно влиять на структуру линейных связей между переменными и приводить к скачкообразному изменению параметров регрессионной модели. В этом случае говорят об исследовании регрессионных моделей с переменной структурой или построении регрессионных моделей по неоднородным данным.

Оценить влияние значений количественных переменных и уровней качественных признаков с помощью одного уравнения регрессии можно путем введения фиктивных переменных.

В качестве фиктивных переменных обычно используются дихотомические (бинарные) переменные, которые принимают всего два значения: «0» и «1». Например, при исследовании зависимости заработной платы от уровня образования Z можно рассмотреть к-1 уровня: начальное образование, среднее и высшее. Обычно вводят (к-1) бинарную переменную. В нашем случае потребуется ввести две фиктивные переменные.

Тогда регрессионная модель запишется в виде:

Где

х1,…хт – экономические (количественные) переменные.

Наличие у работника начального образования будет отражено парой значений z1=0, z2=0.

Параметры при фиктивных переменных z1 и z2 представляют собой разность между средним уровнем результативного признака для соответствующей группы и базовой группы (в нашем примере это работники с начальным образованием).

При построении регрессионных моделей по неоднородным данным необходимо выяснить, действительно ли две выборки однородны в регрессионном смысле, можно ли объединить их в одну и рассматривать единую модель регрессии?

Для ответа на этот вопрос можно воспользоваться тестом Г.Чоу.

По каждой выборке строятся две линейные регрессионные модели:

Проверяемая нулевая гипотеза имеет вид – Н0: b`=b``; D(ε`)= D(ε``)=σ2

Если нулевая гипотеза верна, то две регрессионные модели можно объединить в одну объем n=n1+n2.

Согласно критерию Г.Чоу нулевая гипотеза Н0 отвергается на уровне значимости α, если статистика

Где - остаточные суммы квадратов соответственно для объединенной, первой и второй выборок, n=n1+n2.

Для проверки гипотезы о структурной стабильности тенденции изучаемого временного ряда можно также использовать тест Д.Гуйарати.

 

Тема 4. Нелинейные модели регрессии и их линеаризаци.

 

Довольно часто соотношения между социально-экономическими явлениями и процессами приходится описывать нелинейными функциями. Например, производственные функции (зависимость между объемом производства и основными факторами производства) или функции спроса (зависимость между спросом на товары или услуги и их ценами или доходом).

Следует различать модели, нелинейные по параметрам, и модели, нелинейные по переменным.

Для оценки параметров нелинейных моделей существует два основных подхода:

1. Первый подход основан на линеаризации модели: преобразованием исходных переменных и введением новых, нелинейную модель можно свести к линейной, для оценки параметров которой используется метод наименьших квадратов.

2. Если подобрать соответствующее линеаризующее преобразование не удается, то применяются методы нелинейной оптимизации на основе исходных переменных.

Если модель нелинейна по переменным, то используется первый подход, т.е. вводятся новые переменные, и модель сводится к линейной:

Переходим к новым переменным; и получаем линейное уравнение:

Более сложной проблемой является нелинейность по оцениваемым параметрам. В ряде случаев путем подходящих преобразований эти модели удастся привести к линейному виду. Рассмотрим следующие модели, нелинейные по оцениваемым параметрам:

Степенная (мультипликативная) -

Степенная модель может быть преобразована к линейной путем логарифмирования обеих частей уравнения:

Замена переменных: В новых переменных модель запишется следующим образом:

Степенные модели получили широкое распространение в эконометрическом моделировании ввиду простой интерпретации параметров, которые представляют собой частные коэффициенты эластичности результативного признака по соответствующим факторным признакам.

Экспонента - ,

Экспоненциальная модель линеаризуется аналогично:

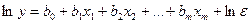
Переходя к новым переменным получаем линейную регрессионную модель:

Гипербола

Гиперболическая модель линеаризуется непосредственной заменой переменной y=1/y:

Эти функции используются при построении кривых Энгеля, которые описывают зависимость спроса на определенный вид товаров или услуг от уровня доходов потребителей или от цены товара.

Логарифмическая модель:

При выборе формы уравнения регрессии важно помнить, что чем сложнее функция, тем менее интерпретируемы ее параметры.

В качестве примера использования линеаризующего преобразования регрессии рассмотрим производственную функцию Кобба-Дугласа:

Где Y – объем производства, К – затраты капитала, L – затраты труда.

Путем логарифмирования обеих частей данную степенную модель можно свести к линейной:

Переходя к новым переменным Y`=lnY, A`=lnA, K`=lnK, L`=lnL, ε`=lnε, получаем линейную регрессионную модель:

Эластичность выпуска продукции.

Показатели α и β являются коэффициентами частной эластичности объема производства Y соответственно по затратам капитала К и труда L. Это означает, что с увеличением только затрат капитала (труда) на 1% объем производства возрастает на α% (β%):

 

Эффект от масштаба производства.

Если α и β в сумме превышают единицу, то говорят, что функция имеет возрастающий эффект от масштаба производства (это означает, что если К и L увеличиваются в некоторой пропорции, то Y растет в большей пропорции). Если их сумма равна единице, то это говорит о постоянном эффекте от масштаба производства. Если их сумма меньше единицы, то имеет место убывающий эффект от масштаба производства. Например, К и L увеличиваются в 2 раза. Найдем новый уровень выпуска (Y*):

Если α+β = 1,2, то 2α+β=2,30, а Y увеличивается больше, чем в 2 раза.

Если α+β = 1, то 2α+β=2, и Y увеличивается также в 2 раза.

Если α+β = 0,8, то 2α+β=1,74, а Y увеличивается меньше, чем в 2 раза.

Первоначально Кобб и Дуглас представляли функцию в виде т.е. предполагали постоянную отдачу от масштаба производства. Впоследствии это допущение было ослаблено.

Если в модели то функцию Кобба-Дугласа представляют в виде:

или

Таким образом, переходят к зависимости производительности труда (Y/L) от его капиталовооруженности (K/L). Логарифмируя обе части уравнения, приводим его к линейному виду:

Функция Кобба-Дугласа с учетом технического прогресса имеет вид:

,

где t — время, параметр — темп прироста объема производства благодаря техническому прогрессу.

Тема 5. Эконометрическое моделирование временных рядов

 

Временным рядом (динамическим рядом) называется набор значений какого-либо показателя за несколько последовательных моментов или периодов времени. Отдельные наблюдения называются уровнями ряда.

Целесообразно выделить следующие 4 типа факторов, под воздействием которых формируются значения элементов временного ряда.

1.Долговременные, формирующие общую (в длительной перспективе) тенденцию в изменении анализируемого признака у(t). Обычно эта тенденция описывается с помощью математической функции . Эту функцию называют трендом.

2.Сезонные, формирующие периодически повторяющиеся в определенное время года колебания анализируемого признака. Обозначим результат действия сезонных факторов с помощью функции . Поскольку эта функция должна быть периодической (с периодами, кратными «сезонам»), в ее аналитическом выражении участвуют гармоники, периодичность которых, как правило, обусловлена содержательной сущностью задачи.

3.Циклические, формирующие изменения анализируемого признака, обусловленные действием долговременных циклов экономической, демографической или астрофизической природы (волны Кондратьева, демографические «ямы», циклы солнечной активности и т.п.).

4.Случайные, не поддающиеся учету и регистрации. Их воздействие на формирование значений временного ряда как раз и обусловливает стохастическую природу элементов уt , а, следовательно, и необходимость интерпретации у1, у2,..., уn как наблюдений, произведенных над случайными величинами, соответственно, , ,..., . Будем обозначать результат воздействия случайных факторов с помощью случайных величин («остатков», «ошибок») .

Конечно, вовсе не обязательно, чтобы в процессе формирования значений всякого временного ряда участвовали одновременно факторы всех четырех типов. Однако во всех случаях предполагается непременное участие случайных факторов.

Выводы о том, участвуют или нет факторы данного типа в формировании значений уt , могут базироваться как на анализе содержательной сущности задачи (т.е. быть априорно-экспертными по своей природе), так и на специальном статистическом анализе исследуемого временного ряда.

Следует отметить, что временные ряды качественно отличаются от простых статистических выборок. Эти отличия следующие:

- последовательные по времени уровни временных рядов являются взаимозависимыми, особенно это относится к близко расположенным наблюдениям;

- в зависимости от момента наблюдения уровни во временных рядах обладают разной информативностью: информационная ценность наблюдений убывает по мере их удаления от текущего момента времени;

- с увеличением количества уровней временного ряда точность статистических характеристик не будет увеличиваться пропорционально числу наблюдений, а при появлении новых закономерностей развития она может даже уменьшаться.

Анализ временных рядов, отражающих развитие экономических процессов, начинается с оценки данных. Уровни исследуемого показателя обязательно должны быть сопоставимы, однородны и устойчивы. Количество наблюдений в них должно быть достаточно велико. Сопоставимость предполагает формирование всех уровней по одной и той же методике, использование одинаковой единицы измерения и шага наблюдений.

Самым распространённым способом моделирования тенденций временного ряда является построение аналитической функции характеризующей зависимость уровней ряда от времени или тренда.

Временные ряды наблюденных показателей чаще всего аппроксимируются следующими элементарными функциями: y=a+b1*t (уравнение прямой линии); y=a+b1*t+b2*t2 (парабола 2-го порядка); y=a+b1*t+b1*t2+b3*t3 (парабола 3-го порядка); y=a+b*ln(t) (логарифмическая); y=a*tb (степенная); y=a*bt (показательная); y=a+ (гиперболическая); y=1/(a+b*e-t) (логистическая); y=sin t и y=cos t (тригонометрическая). Возможно использование комбинированных функций.

Некоторые социально-экономические процессы и объекты моделируются на основе тренда с помощью определенных функций. Например, демографические модели, модели спроса, модели урожайности и т.д.

Приведем примеры функций, которые используются для моделирования спроса:

1.у = а – функция спроса не зависит от времени;

2.у = a + bt – функция спроса линейно зависит от времени;

3. - функция спроса циклично (периодично) зависит от времени;

4. - функция спроса линейно-циклично меняется во времени.

Выделение тренда может быть произведено тремя методами: скользящей средней, укрупнения интервалов или аналитического выравнивания.

Под аналитическим выравниванием, которое используется наиболее часто, подразумевается определение основной проявляющейся во времени тенденции развития изучаемого явления.

Параметры каждого из перечисленных выше трендов можно определить обычным МНК, используя в качестве независимой переменной время t = 1, 2, ….n, а в качестве зависимой переменной – фактические уровни временного ряда уt. Для нелинейных трендов предварительно проводят стандартную процедуру их линеаризации.

Выбранная прогнозная эмпирическая функция, описывающая динамический ряд, должна минимизировать стандартное отклонение S на интервале оценивания, обеспечивать тесноту связи (по коэффициенту корреляции); аппроксимирующее уравнение должно быть адекватно фактической временной тенденции (по F-критерию) и устранять автокорреляцию.

Технология моделирования на основе тренда включает следующие этапы.

1.Анализ и обработка исходной информации.

2.Выбор вида функции, описывающей временной ряд.

3.Расчет параметров функции (например, методом наименьших квадратов).

4.Оценка адекватности и достоверности уравнения тренда.

Оценка адекватности проводится с помощью показателей рассмотренных в теме 2, так как трендовые модели являются частным случаем регрессионных моделей. Следует отметить, что временные ряды качественно отличаются от простых числовых выборок, поэтому обычно в целях проверки адекватности модели используют оценку устойчивости тенденции временного ряда.

Определение устойчивости изменения показателей временного ряда

Устойчивость характеризуется преобладанием закономерности над случайностью в изменении уровней ряда. Устойчивость экономических процессов можно рассматривать как категорию противоположную колеблемости, и как устойчивость направленности изменений.

В первом случае показатель устойчивости можно измерять как разность между единицей и относительным показателем колеблемости. В свою очередь показатель колеблемости вычисляется как отношение среднеквадратического отклонения от тренда к среднему значению показателя.

, где

- показатель колеблемости уровней временного ряда;

- среднеквадратическое отклонение уровней временного ряда от рассчитанных по уравнению тренда (стандартное отклонение);

- среднее значение уровней временного ряда;

- фактические значения уровней временного ряда;

- значения уровней временного ряда, рассчитанные по уравнению тренда.

Следовательно, показатель устойчивости будет равен:

Показатель устойчивости характеризует близость фактических уровней к тренду. Изменения показателей считаются устойчивыми, если показатель устойчивости не менее 67% (то есть показатель колеблемости не превышает 33%).

Во втором случае устойчивость характеризует уровни временного ряда как процесс их направленного изменения. С этих позиций полной устойчивостью направленного изменения уровней временного ряда следует считать такое их изменение, в процессе которого каждый следующий уровень либо выше всех предшествующих (устойчивый рост), либо ниже всех предшествующих (устойчивое снижение). Всякое нарушение строго ранжированной последовательности уровней свидетельствует о неполной устойчивости их развития.

При такой интерпретации в качестве показателя устойчивости тенденции можно использовать коэффициент корреляции рангов Ч.Спирмена:

, где

n – число уровней временного ряда;

- разность рангов уровней и номеров периодов времени.

Коэффициент корреляции рангов Спирмена изменяется от -1 до 1. При хаотическом чередовании подъемов и падений исследуемого процесса его значение буде близко к нулю. Значение коэффициента близкое к 1 доказывает устойчивость тенденции возрастания, близость коэффициента к -1 свидетельствует об устойчивой тенденции убывания.


Решение типовой задачи на построение регрессионной модели

 

По данным, представленным в таблице 1, изучается зависимость балансовой прибыли предприятия торговли Y (тыс. руб.) от следующих факторов:

X 1 - объем товарных запасов, тыс. руб.;

X 2 - фонд оплаты труда, тыс. руб.;

X 3 - издержки обращения, тыс. руб.;

X4 - объем продаж по безналичному расчету, тыс. руб.

Таблица 6.1.

Месяц У Х1 Х2 Х3 Х4
41321,57 300284,10 19321,80 42344,92 100340,02
40404,27 49107,21 20577,92 49000,43 90001,35
37222,12 928388,75 24824,91 50314,52 29301,98
37000,80 724949,11 28324,87 48216,41 11577,42
29424,84 730855,33 21984,07 3301,30 34209,84
20348,19 2799881,13 11000,02 21284,21 29300,00
11847,11 1824351,20 4328,94 28407,82 19531,92
14320,64 1624500,80 7779,41 40116,00 17343,20
18239,46 1115200,93 18344,11 32204,98 4391,00
22901,52 1200947,52 20937,31 30105,29 14993,25
27391,92 1117850,93 27344,30 40294,40 104300,00
44808,37 1379590,02 31939,52 42239,79 119804,33
40629,28 588365,77 29428,60 55584,35 155515,15
31324,80 434281,91 30375,82 49888,17 60763,19
34847,92 1428243,59 33000,94 59866,55 8763,25
33241,32 1412181,59 31322,60 49975,79 4345,42
29971,34 1448274,10 20971,82 3669,92 48382,15
17114,90 4074616,71 11324,93 26032,95 10168,00
8944,94 1874298,99 8341,52 29327,21 22874,40
17499,58 1525436,47 10481,14 40510,01 29603,05
19244,80 1212238,89 18329,90 37444,69 16605,16
34958,32 1154327,22 29881,52 36427,22 32124,63
44900,83 1173125,03 34928,60 51485,62 200485,00
57300,25 1435664,93 41824,92 49959,92 88558,62

Задание:

1. Для заданного набора данных постройте линейную модель множественной регрессии.

2. Оцените точность и адекватность построенного уравнения регрессии.

3. Выделите значимые и незначимые факторы в модели.

4. Постройте уравнение регрессии со статистически значимыми факторами. Дайте экономическую интерпретацию параметров модели.

5.Для полученной модели проверить выполнение условия гомоскедастичности остатков, применив тест Голдфельда-Квандта.

6.Проверить полученную модель на наличие автокорреляции остатков с помощью теста Дарбина-Уотсона.

 

Решение.

Для получения отчета по построению модели в среде EXCEL необходимо выполнить следующие действия:

1. В меню Сервис выбираем строку Анализ данных. На экране появится окно

 

Рис. 6.1. Анализ данных

2. В появившемся окне выбираем пункт Регрессия. Появляется диалоговое окно, в котором задаем необходимые параметры.

3. Диалоговое окно заполняется следующим образом:

Входной интервал Y - диапазон (столбец), содержащий данные со знамениями объясняемой переменной;

Входной интервал X - диапазон (столбцы), содержащий данные со значениями объясняющих переменных.

Метки - флажок, который указывает, содержат ли первые элементы отмеченных диапазонов названия переменных (столбцов) или нет;

Константа-ноль - флажок, указывающий на наличие или отсутствие свободного члена в уравнении регрессии ( );

Выходной интервал - достаточно указать левую верхнюю ячейку будущего диапазона, в котором будет сохранен отчет по построению модели;

Новый рабочий лист - можно задать произвольное имя нового листа, в котором будет сохранен отчет.

Если необходимо получить значения и графики остатков (еi), установите соответствующие флажки в диалоговом окне. Нажмите на кнопку ОК.

Вид отчета о результатах регрессионного анализа представлен на рис. 6.2.

Рис. 6.2. Вывод итогов

Рассмотрим таблицу "Регрессионная статистика".

Множественный R - это , где R2 - коэффициент детерминации.

R-квадрат — это R2. В нашем примере значение R2 = 0,8178 свидетельствует о том, что изменения зависимой переменной Y (балансовой прибыли) в основном (на 81,78%) можно объяснить изменениями включенных в модель объясняющих переменных – X1, Х2, X3, X4. Такое значение свидетельствует об адекватности модели.

Нормированный R-квадрат - поправленный (скорректированный по числу степеней свободы) коэффициент детерминации.

Стандартная ошибка регрессии S = , где S2 = - необъясненная дисперсия (мера разброса зависимой переменной вокруг линии регрессии); п — число наблюдений (в нашем примере равно 24), т - число объясняющих переменных (в нашем примере равно 4).

Наблюдения - число наблюдений п.

Рассмотрим таблицу с результатами дисперсионного анализа.

df - degrees of freedom - число степеней свободы связано с числом единиц совокупности п и с числом определяемых по ней констант (m+1).

55 - sum of squares - сумма квадратов (регрессионная (RSS-regression sum of squares), остаточная (ESS — error sum of squares) и общая (TSS— total sum of squares), соответственно). MS-mean sum - сумма квадратов на одну степень свободы.

F - расчетное значение F-критерия Фишера. Если нет табличного значения, то для проверки значимости уравнения регрессии в целом можно посмотреть Значимость F. На уровне значимости уравнение регрессии признается значимым в целом, если Значимость F < 0.05, и незначимым, если Значимость F 0.05.

Для нашего примера имеем следующие значения (таблица 6.2.)

Таблица 6.2.

Результаты дисперсионного анализа

  df SS MS F Значимость F
Регрессия m = 4 RSS=2,82E+09 RSS/df=7,04E+08 21,32 8,28E-07
Остаток n-m-1=19 ESS=6,27E+08 ESS/df=3,30E+07    
Итого n-1 = 23 TSS=3,44E+09      

 

Расчетное значение F-критерия Фишера составляет 21,32.

Значимость F= 8,28Е-07, что меньше 0,05. Таким образом, полученное уравнение в целом значимо.

В таблице 6.3. приведены значения параметров (коэффициентов) модели, их стандартные ошибки и расчетные значения t-критерия Стьюдента для оценки значимости отдельных параметров модели.

Таблица 6.3.

Оценка коэффициентов регрессии

  Коэффициенты Стандартная ошибка t-статистика Р-Значение Нижние 95% Верхние 95%
Y b0 = 7825.51 mb0=5350.78 tb0 = 7825.51 / 5350.78 = = 1,4625 0.1599 -3373.80 b0 19024.83
X1 b1=-0.00098 mb1=0.00172 tb1=-0.569 0.5762 -0,0046 b1 0,0026
X2 b2=0.8806 mb2=0.15891 tb2=5.5417 0.00002 0,5480 b2 1,2132
X3 b3=0.0094 mb3=0.09754 tb3=0.0961 0.9244 -0,1948 b3 0,2135
X4 b4=0.0617 mb4=0.02647 tb4=2.3312 0.0309 0,0063 b4 0,1171

 

Анализ таблицы 6.3. позволяет сделать вывод о том, что на уровне значимости = 0.05 значимыми оказываются лишь коэффициенты при факторах X2 и Х4, так как только для них Р-значение меньше 0,05. Таким образом, факторы X1 и Х3не существенны, и их включение в модель нецелесообразно.

Поскольку коэффициент регрессии в эконометрических исследованиях имеют четкую экономическую интерпретацию, то границы доверительного интервала для коэффициента регрессии не должны содержать противоречивых результатов, как, например -0,1948 b3 0,2135. Такого рода запись указывает, что истинное значение коэффициента регрессии одновременно содержит положительные и отрицательные величины и даже ноль, чего не может быть. Это также подтверждает вывод о статистической незначимости коэффициентов регрессии при факторах X1 и Х3.

Исключим несущественные факторы X1 и Х3и построим уравнение зависимости Y (балансовой прибыли) от объясняющих переменных X2 и Х4. Результаты регрессионного анализа приведены в таблицах 6.4., 6.5., 6.6.

 

 

Таблица 6.4.

Регрессионная статистика

Множественный R 0,9024465
R-квадрат 0,8144098
Нормированный R-квадрат 0,7967345
Стандартная ошибка 5515,53984
Наблюдения

 

 

Таблица 6.4.

Дисперсионный анализ

df SS MS F Значимость F
Регрессия 46,076253 2,08847E-08
Остаток 638844774,1 30421179,72    
Итого      

 

Таблица 6.4.

Оценка коэффициентов регрессии

Коэффициенты Стандартная ошибка t-статистика P-Значение Нижние 95% Верхние 95%
Y-пересечение 5933,1025 2844,611998 2,085733487 0,0493883 17,40698 11848,798
Переменная X 2 0,9162546 0,132496978 6,915286693 7,834E-07 0,640712 1,1917972
Переменная X 4 0,0645183 0,024940789 2,58686011 0,0172036 0,012651 0,1163856

 

Оценим точность и адекватность полученной модели.

Значение R2 = 0,8144 свидетельствует о том, что вариация зависимой переменной Y (балансовой прибыли) по-прежнему в основном (на 81,44%) можно объяснить вариацией включенных в модель объясняющих переменных – Х2 и Х4.Это свидетельствует об адекватности модели.

Значение поправленною коэффициента детерминации (0,7967) возросло по сравнению с первой моделью, в которую были включены все объясняющие переменные (0,7794).

Стандартная ошибка регрессии во втором случае меньше, чем в первом (5515 < 5745).

Расчетное значение F-критерия Фишера составляет 46,08. Значимость F = 2.08847Е-08, что меньше 0,05. Таким образом, полученное уравнение в целом значимо.

Далее оценим значимость отдельных параметров построенной модели. Из таблицы 3 видно, что теперь на уровне значимости = 0.05 все включенные в модель факторы являются значимыми: Р-значение < 0,05.

Границы доверительного интервала для коэффициентов регрессии не содержат противоречивых результатов:

с надежностью 0.95 (с вероятностью 95%) коэффициент b1 лежит в интервале 0.64 b1 1,19;

- с надежностью 0.95 (с вероятностью 95%) коэффициент b2 лежит в интервале 0,01 b2 0,12

Таким образом, модель балансовой прибыли предприятия торговли запишется в следующем виде:

= 5933,1 + 0,916*Х2+ 0,065*Х4

Параметры модели имеют следующую экономическую интерпретацию. Коэффициент b1 = 0,916, означает, что при увеличении только фонда оплаты труда (X2)на 1 тыс. руб. балансовая прибыль в среднем возрастает на 0,916 тыс. руб., а то, что коэффициент b2 = 0,065, означает, что увеличение только объема продаж по безналичному расчету (Х4) на 1 тыс. руб. приводит в среднем к увеличению балансовой прибыли на 0,065 тыс. руб. Как было отмечено выше, анализ Р-значений показывает, что оба коэффициента значимы.

Средние коэффициенты эластичности рассчитываются по формуле, приведенной выше в теме 2.

Эх1=0,53*35,75/88,38=0,214

Согласно коэффициенту эластичности по первому фактору - рост цены на 1% приводит к увеличению объема предложения на 0,214%.

Эх2=-9,89*5,44/88,38=-0,609

Второй средний коэффициент эластичности доказывает снижение объема предложения блага на 0,609% при увеличении заработной платы сотрудников фирмы на 1%.

Для выполнения задания 5 снова воспользуемся “Пакетом анализа”, встроенным в EXCEL.

В соответствии со схемой теста Голдфельда-Квандта упорядочим данные по возрастанию переменной X4, предполагая, что дисперсии ошибок зависят от величины э