Вероятность и закон нормального распределения вероятностей

Вероятность (Р) – действительное число в диапазоне от 0 до 1,приписываемое случайному событию, представляющее отношение количества благоприятных случаев (n) ко всему количеству возможных случаев (N) в данной совокупности случаев:

При n=0

при n=N

cобытие становится неслучайным, а погрешность становится систематической.

При Р 0,5 событие считается маловероятным, при Р 0,5- вероятным. Чем больше N,тем больше вероятность и достоверность события. При N, стремящемся к бесконечности, Р стремится к 1 (закон больших чисел).

Теория вероятностей содержит несколько законов распределения. Чаще других имеет место закон нормального распределения вероятностей, или закон Гаусса.

Рис. 2 Кривые распределения случайных погрешностей:

а – по закону Гаусса; б – по равновероятностному; в – по закону треугольника; г – по закону Максвелла; 1 – при особо точных методах; 2 – форма кривой при точных методах обработки и измерения; 3 – при низкой точности

Закон Гаусса действует при большом количестве относительно малых , равнозначных, равновозможных и равновлияющих независимых факторов (т.е. когда нет преобладающих факторов).Этот закон проявляется при изготовлении изделий на настроенном автоматизированном оборудовании в условиях массового и серийного производств, а также при линейных измерениях.

Если учитывать только случайные погрешности в чистом виде, то закон Гаусса можно представить графически (рис.2) в виде теоретической кривой нормального распределения (кривой плотности распределения вероятности), где у - плотность вероятности, или частость (отношение количества благоприятных событий к количеству всех событий); в нашем случае частота появления -й составляющей случайной погрешности: 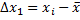-остаточная -я погрешность, или погрешность отдельного -го измерения, характеризующая отклонение случайной величины о центра группирования (центр группирования – ось у), где =1,2,…n-порядковые номера деталей в партии или порядковые номера измерений: -параметр -й детали партии или результат -го измерения; -средний арифметический параметр партии деталей или средний арифметический результат измерений (опытов), соответствующий центру группирования параметров детали в партии или результатов измерений (которое при неограниченном числе измерений называется математическим ожиданием М(х)).

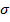-средняя квадратическая погрешность, которая характеризует зону рассеяния- разброса случайных величин относительно центра группирования (в знаменателе n, если n 25;n-1,если n 25).

Рис. 3

Кривая Гаусса (нормального распределения) описывается уравнением:

где - основание натурального логарифма.

Из формы кривой видно, что большие отклонения появляются значительно реже, чем малые, а появление очень больших отклонений маловероятно. Поэтому принимаемые в расчет погрешности ограничиваются некоторыми предельными значениями , где V-размах или поле рассеяния случайных погрешностей, определяемое как разность между наибольшими и наименьшими померенными размерами в партии деталей.

Теоретическая кривая нормального распределения обладает таким свойством, что если площадь, заключенную между кривой и осью абсцисс, принять за 100% (или равной 1), то площадь, заключенная между частью кривой и отрезком составит , между частью кривой и отрезком в пределах 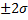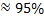от всей площади (доверительная вероятность измерения), между частью кривой и отрезком от всей площади (доверительная вероятность технологическая). Распределение этих площадей соответствует распределению случайных величин.

Величина называется предельной (допустимой) случайной технологической погрешностью, в дальнейшем мы будем называть технологическим допуском. А зона рассеяния погрешностей, соответствующая величине , называется полем рассеяния технологических погрешностей. Площадь, оставшаяся за пределами , равна 0,27% (за правой и левой ветвями кривой по 0,135%).Следовательно, с вероятностью, весьма близкой к 100% (К1), можно утверждать, что случайные погрешности параметров достаточно большой партии деталей не будут выходить за пределы , а вероятность появления брака составит 0,27%, что, как правило, допустимо (0,27% составляет 3 детали из 1000 ил 27 из 10000).

Технологические погрешности параметров, превышающие , и погрешности измерений, превышающие 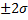, относят к грубым.

Анализируя кривую Гаусса, можно сделать следующие выводы:

- малые по величине погрешности встречаются значительно чаще, чем большие (сила мелочей в том, что их много, и потому они могут приводить к большим отрицательным последствиям);

- одинаковые по абсолютной величине, но противоположные по знаку погрешности встречаются одинаково часто;

- большинство параметров партии деталей или результатов измерений и их погрешностей группируются около середины поля рассеяния (центра группирования случайных величин, т.е. имеют погрешности, стремящиеся к нулю, но не равные нулю);

- с увеличением количества деталей или измерений среднее арифметическое из случайных величин данного ряда стремится к нулю (благодаря чему, увеличивая количество измерений одной величины, можно уменьшать влияние случайных погрешностей на результаты измерений, практически исключая их);

- наиболее достоверные значения результатов при многократных измерениях представляют собой средние арифметические из полученных результатов;

- технологические погрешности, выходящие за пределы , признаются грубыми;

- погрешности измерений, выходящие за пределы 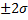, признаются грубыми и исключаются из результатов измерений.

По форме кривой Гаусса можно сравнивать параметры и результаты измерений по точности. Чем выше и сжата кривая, тем точность выше.

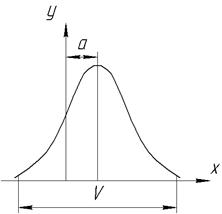
Рис. 4

Как уже отмечалось, одновременно имеют место как систематические, так и случайные погрешности, поэтому форма и расположение кривой распределения изменяются (рис.4). Систематические постоянные по величине и знаку погрешности смещают центр группирования относительно оси ординат (т.е. а 0-величина смещения).