Действия сложения и вычитания в пределах 100

 

Как и во время изучения первого десятка, приемы сложения и вычитания в пределах 100 раскрывают в органической связи с учения теоретического материала. При таком подходе ученики лучше усваивают вопрос теории, потому что они их применяют, и быстрее формируются более сознательные вычислительные навыки.

Анализ приемов сложения и вычитания чисел в пределах 100 свидетельствует, что для сознательного выполнения их ученики должны хорошо знать нумерацию чисел в пределах 100, таблицу сложения и соответствующие случаи вычитания в пределах 10 и, кроме того, усвоить такие особенности действий вычитания и сложения : сложение числа к сумме, вычитание числа из суммы, прибавление суммы к числу, вычитание суммы от числа, прибавление суммы к сумме и вычитанию суммы из суммы.

Сложение и вычитание рассматривают в таком порядке.

Во П классе сначала изучают сложение и вычитание круглых чисел(70+20, 60-40). Потом рассматривают свойства сложения числа к сумме, пользуясь которой и раньше усвоенными знаниями, вводят приемы для случаев: 46+20, 46+2. Здесь же, используется прием перестановки слагаемых, рассматривают случаи 2+46. Дальше изучают свойство вычитания числа из суммы и приемы для случаев: 48-30, 48-3 и 40-3. Потом рассматривают свойство прибавления суммы к числу, на основании какой раскрывают табличные случаи сложения с переходом через десяток(9+3). После этого изучают свойство вычитания суммы из числа и табличные случаи вычитания(12-5). Наконец, рассматривают парами приемы сложения .и вычитания, какие базируются на двух последних свойствах: 47^110 и 47-9; 30+12 и ЗО-12; 65+14 и 65-14; 36+19 и 36-19. В II классе изучают свойства прибавления суммы к сумме и вычитанию суммы из сумми, на основе которых вводят приемы поразрядного сложения и вычитания.

Рассмотрим подробнее методику изучения свойств и вычислительных приемов.

60 - 40

Сложение и вычитание круглых десятков(двузначных разрядных чисел) сводится к сложению и вычитания однозначных чисел, которые выражают число десятков. На-пример, чтобы к 50 прибавить ЗО, достаточно до 5 десяткам прибавить 3 десятка, будет 8 десятков, или 80, а, чтобы из 50 вычесть ЗО, достаточно из 5 десятков вычесть 3 десятка, будет 2 десятка, или 20. Объяснение решение двух-трех примеров иллюстрирующих рисунками и такой записью:

6 дес.- 4 дес.= 2дес. 60 - 40 = 20

70 + 20

7 дес.+ 2 дес.= 9 дес.

70+20 = 90

Дальше, на следующих двух-трех уроках, ученики объясняют вслух, а потом в мысли. В результате упражнений у учеников постепенно производится навык.

Введению свойства прибавления числа к сумме должна предшествовать специальная подготовительная работа, вследствии которой ученики знакомятся с математическими выражениями "сумма чисел.". и "разница чисел."., учатся читать и записывать выражения со скобками, заменять двузначные неразрядные числа суммой их разрядных слагаемых.

Эти вопросы рассматривают во время изучения сложения и вычитания чисел в пределах 10 и нумерации чисел в пределах 100.

Каждое свойство изучают примерно за однако-вим планом: сначала, используя наглядные пособия, надо раскрыть суть самого свойства, потом научить детей застосову-вати ее во время выполнения разных упражнений учебного характера и, наконец, научить, пользуясь знанием свойства, находить рациональные приемы вычислений с учетом особенностей кож-ного конкретного случая.

Рассмотрим, как можно ознакомить детей со свойством к-. дача числа к сумме.

Раскрывая содержание свойства, надо показать детям, что число к сумме можноприбавить разными способами: можно вычислить сумму и к найденному результату прибавить число, можно прибавить число к первому слагаемому и к найденному результату прибавить второе слагаемое, а можно прибавить число ко второму слагаемому и найденный результат прибавить к первому слагаемому.

Покажем, как это можно сделать.

Учитель записывает на доске выражение (5+3)+2.

Прочитайте пример. (К сумме чисел 5 и 3 прибавить 2.) Назовите сумму. (5 плюс 3.) Назовите первое слагаемое этой суммы. (5.) Назовите второе слагаемое. (3.) Назовите число, которое надо прибавить к этой су-ми. (2.) Как найти результат? (Вычислю сумму, будет 8; прибавлю 2, будет 10.)

На доске запись:+2 = 8+2= 10.

Сегодня вы научитесь прибавлять число к сумме и другими способами.

Учитель вывешивает на доске рисунки двух гаражей и предлагает ученикам изготовить прямоугольники голубого, зеленого и красного цветов, вырезанные из бумаги. Это машины. Количество машин в первом гараже будет изображать первое слагаемое. Сколько машин нужно по-ставити в первый гараж? (5.)

Учитель вставляет в прорези 5 машин голубого цвета, вырезанные из картона, а ученики раскладывают на партах 5 голубых прямоугольников.

Количество машин во втором гараже будет изображать второе слагаемое. Сколько машин поставим во второй гараж? (3.)

Учитель "ставит" во второй гараж 3 зеленых машины, а деть роз-кладають на партах 3 зеленых прямоугольника.

Приехали еще две машины(прикрепляют к доске две красных машины, а ученики кладут на парту два красных прямоугольника).

На доске размещают рисунки(рис. 15).

Красные машины надо поставить в гараж. В какой гараж их можно поставить? (В первый или во второй?) Поставим их в первый гараж. (Учитель "ставит" машины в первый гараж, а деть прису-вають красные прямоугольники к голубым). Как теперь узнаем

 

 

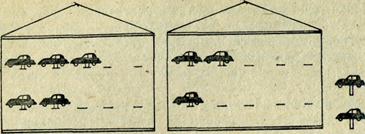
сколько всех машин? (До 5 прибавить 2, будет 7, и еще прибавить 3, будет 10). Да, число 2 прибавили до 5, первого доданка, потом к знай-деного результату, до 7, прибавили второе слагаемое 3. Сравните ответы (Достали также 10.) Если достанем столько же* сколько во время решения первым способом, то, следовательно, можно прибавить число к сумме и таким способом. Кто расскажет, как добавляли число к сумме? (Ученик рассказывает).

Аналогично с использованием тех же пособий раскрывают еще один способ: можно прибавить число ко второму доданка - к Из и найденный результат прибавить к первому доданка - до 5.

Сколько способов прибавления числа к сумме мы рассмотрели? (Три.) Да, три способа: можно решить пример так, как и рраньше это делали, - вычислить сумму чисел 5 и 3 и к результату, до 8, прибавить число 2; можно прибавить число 2 к первому доданка, до 5, и к найденному результату, до 7, прибавить второе слагаемое 3; а можно прибавить число 2 ко второму доданка, до 3, и найден ре-зультат, 5, прибавить к первому доданка, до 5.

Так же рассматривают развязывание тремя способами еще од-ного приложу на добавление числа к сумме. При этом викори-стовують то же наглядное пособие.

Во время изучения свойства можно использовать и другие посіб-ники, например: в ведра вливать воду литрами, в конверты вклада-ти открытки, в тарелки раскладывать фрукты и тому подобное. -

На следующем уроке, рассматривая три способа добавления чис-ла к сумме, одновременно с использованием наглядных пособий роб-лять развернутая запись. Эту запись учитель выполняет на доске или на плакате, а ученики в тетрадях. Например, развязывание тремя способами примера +3 надо записать так:

1) (4+2) +3-6+3=9;

2) (4+2) +3-(4+3) +2 = 7+2-9;

3) (4+2) +3 = 4+ (2+3) =4 + 5=9.

Каждую запись ученики объясняют сначала под руководством учи-теля, а потом самостоятельно. На этом этапе не надо требовать от детей обобщенной формулировки правил добавления числа к сумме; достаточно, -, чтобы они умели объяснять решение разными способами определенных конкретных примеров.

Так же прорабатывают и другие свойства. Однако с рассмотрением новых свойств часть самостоятельного участия детей в "открытии" разных способов нахождения результатов должна увеличиваться.

Свойства, которые дети формулируют в виде правил(и .нази-вають правилами), изучают, применяя их во время выполнения специальных упражнений. Это - нахождение значений заданных выражений разными способами и самым удобным способом, превращение вира-зів, развязывание задач разными способами и тому подобное.

Например, усвоению свойства добавления числа к сумме будут способствовать такие упражнения:

1. Прочитайте пример и вычислите результат разными способами :

а) Вычислю сумму и прибавлю к ней число 2 :

(6+ 1) +2 = 7 + 2 = 9.

б) Прибавлю число 2 к 6, к первому доданка, и к найденному результату, к8, прибавлю второе слагаемое - 1:

(6 + 1) + 2 = (6 + 2) + 1 = 8 + 1 = 9.

в) Прибавлю число 2 к 1, ко второму слагаемому, и найденный результат прибавлю к первому слагаемому – к 6:

(6 + 1) + 2 = 6 + (1 + 2) .= 6 + 3 = 9.

2. Найдите результат удобным способом:

(8 + 6) + 4 (30 + 7) + 20 (60 + 3) + 4.

Выполняя такие упражнения, ученики в уме воссоздают все три спо-соби нахождения результата и выбирают самый рациональный. Сначала учитель должен пытаться, чтобы дети выбрали такой способ самостоятельно. Например, определяя значение первого вира-зу, учитель говорит, что более легко(лучше) прибавить 4 к тому числу, при добавлении к которому достанем круглое число, потому что к круглому чис-ла более легко добавлять; находя значение двух других выражений, учи-тель подчеркивает, что десятки удобнее добавлять до десятков, а віди-ниці к единицам.

3. Закончить запись:

(8+ 7)+2= (8 + 2)... (40 + 3) +5 = 40+ (...).

Учитель дает приблизительно такое объяснение: слева записано, что к сумме чисел 8 и 7 надо прибавить 2, а справа записано, что число 2 до-дали до 8, к первому доданка; чтобы справа достать столько, скіль-ки слева, надо к найденной сумме прибавить второе слагаемое 7.

Усвоению свойств помогает также решение некоторых задач разными способами и сравнение решений.

Как только будет усвоенное свойство, можно переходить к изучению вычислительных приемов, которые основываются на соответствующем свойстве.

Рассмотрим, как можно провести работу над прийома-ми для случаев: 46+20 и 46+2, которые рассматривают потом за-своєння учениками свойства добавления числа к сумме.

Для подготовки предлагают развязать самым удобным спо-собом примеры вида :+40 и+2. Решая такие примеры, ученики должны выяснить, во-первых, что десятки удобнее добавлять до десятков, а единицы к единицам, и, во-вторых, что в пер-шому, случая добавляли 40 к числу 53, а во втором - 2 добавляли до 36.

Во время ознакомления с приемом надо, производя соответствующие действия, использовать наглядность и сопровождать их від-повідними записями и словесными объяснениями.

На доске запись: 46+20. Дети читают пример и иллюстрируют числа с помощью полосок с кружками или паличок-всі у себя на партах, а один ученик на доске(см. рис. 16).

Суммой каких разрядных слагаемых замінимо число 46? (40 и 6). Покажите, как изображены эти слагаемые. (Показывают полоски.) Заміни-мо число 46 суммой разрядных слагаемых. Запись на доске: 46+20 +20.

Прочитайте пример. (К сумме чисел 40 и 6 прибавить 20.) Как удобнее вычислить результат? (Прибавить число 20 до 40, к пер-шого доданка, и к найденному результату прибавить.6, второй дода--нок.

Выполним это на полосках. (До 4 полосок присовывают 2 такие же полоски и еще 6 кружков.) Вычислите результат. (До 40 до-дати 20, будет 60; до 60 прибавить 6, будет 66.)

Запись: 46+20 +20 +6 = 66. Аналогично рассматривают случай 462.

Теперь полезно выяснить, чем похожи способы решения(в обоих случаях заміняли первое число суммой разрядных слагаемых и к сумме прибавляли число) и чем отличаются(в первом примере прибавляли десятки, их удобнее прибавить к десяткам, а во втором примере прибавляли единицы, их удобнее прибавлять к единицам).

Чтобы не допустить неправильных обобщений, надо сказать детям, что здесь заменяли суммой первое число(46), а в других случае удобнее заменять суммой второе число.

Потом можно рассмотреть, используя иллюстрации, решения с объяснением аналогичных примеров, после чего решить ряд примеров с развернутой записью и подробным объяснением сначала под руководством учителя, а потом самостоятельно.

Очень важно с самого начала научить детей выделять во время объяснения примеров главные моменты, то есть надо добиться, чтобы ученик рассуждал по определенному плану. Да, уже на втором уроке учитель может сказать, что такие примеры решать более легко, если рассуждать будем в определенном порядке: сначала заменим число суммой, потом прочитаем пример, а дальше решим его удобным способом.

Вот как должен рассуждать ученик, решая пример 23+4: "Заменю число 23 суммой разрядных слагаемых 20 и 3; получим пример: к сумме чисел 20 и 3 прибавить 4; решим его удобным способом, здесь более удобное число 4 прибавить до 3, ко второму доданка, будет 7, прибавлю найденный результат до 20, к первому сагаемому, будет 27".

Одновременно записывают:

23 + 4 = (20 + 3) + 4 = 20 + (3 + 4) = 27.

Так рассуждают сначала под руководством учителя, который сообщает план объяснения, записав на доске слова: заменю будет пример.., удобнее.. Постепенно дети овладевают такой последовательностью операций : выполняют и называют их самостоятельно. Это обеспечивает в будущем самостоятельный выбор учениками новых вычислительных приемов

Подробное объяснение решения, которое дают ученики, нужно постепенно сокращать. Например, уже на втором уроке одновременно с подробным объяснением и развернутой записью дети так объясняют решение примера 56+30:

56 - это 50 и 6, прибавлю ЗО к 50, будет 80, да еще 6, будет 86. Впоследствии объяснение становится еще более коротким: 50 и ЗО -это 80, и 6, всего 86. Однако время от времени надо требовать подробного объяснения иногда с развернутым объяснением, чтобы дети, натолкнувшись на трудности, всегда могли воссоздать всю последовательность операций.

На следующих уроках рассматривают случаи: 27+3 и 6+42, которые принципиально не отличаются от ранее рассмотренных, потому ученики са-мостоятельно дают объяснение. В первом случае сумма единиц образует десяток, его надо прибавить к десяткам; во втором - нужно слагаемые переставить местами (этот прием дети уже знают).

Как только дети усвоят вычислительный прием, надо на специальних упражнениях сформировать вычислительные навыки. Навык производится в результате тренировки, потому на каждом уроке надо давать примеры как для устной, так и для письменной работы. При этом новые случаи следует рассматривать рядом с раньше изученными.

Одновременно с работой над формированием вычислительных навыков для рассмотренных случаев изучают свойство вычитания числа от суммы по такой же методике, как и свойствоприбавления числа к сумме. Как только ученики усвоят его, вводят сначала одновременно приемы для случаев: 57-ЗО и 57 - Из, а немного позже - прием для случая 60-3.

Чтобы подготовить детей к раскрытию первых двух приемов, предлагают решить самым удобным способом примеры вида :(60+ +8) - 50 и(60+8) - 5. Выполняя такие задания, ученики замечают, Что здесь удобнее единицы вычитать от единиц, а десятки от десятков.

Новые приемы для случаев 57-30 и 57-3 решают примерно так же, как и аналогичные приемы сложения. При этом ученики должны под руководством учителя, но с большей самостоятельностью, дать объяснение согласно приведенному раньше плану. Приведем рассуждения ученика :

57-ЗО. Заменю число 57 суммой разрядных слагаемых 50 и^ 7; плучили пример: от суммы чисел 50 и 7 отнять ЗО; лучше вычесть ЗО из 50, из первого слагаемого, а к найденному результату, к 20, прибавить 7, второе слагаемое, будет 27.

Запись: 57-30=(50+7) - ЗО = (50-30)+7=27.

Аналогичное объяснение дают для случая 57-3.

Выражение 60-3 отличается от предыдущего тем, что здесь уменьшаемое является разрядным числом и его нельзя заменить суммой разрядных слагаемых. Определяя результат, удобнее уменьшаемое заменить суммой таких двух слагаемых, один из которых равняется 10. Такие слагаемые называют "удобными"(разрядные слагаемые также удобны). Чтобы научить детей выделять такие удобные слагаемые, используют специальные упражнения:

1) Заменить число суммой по образцу:

ЗО = 20 + 10, 40 '=. П + 10, 90 = П + 10, 50 = П + 10.

2) Решите примеры удобным способом:

((50+1.0) - 7,(90+10) - 3.

От какого числа отняли 7? Из?

При ознакомлении с приемом используют щепотки палочек(один пучок решают).

Ученики дают такое объяснение:

60-3. Заменю число 60 суммой удобных слагаемых 50 и 10; получили пример: от суммы чисел 50 и 10 отнять 3; удобнее отнять 3 от 10, от второго слагаемого, и найденный результат(7) прибавить к 50, к первому слагаемому, будет 57.

Запись: 60-3= (50+10) - 3 = 50 + (10-3) =57.

Потом решают упражнения для выработки вычислительных навыков. Одновременно изучают свойство добавления суммы к числу, равно как и раньше рассмотренные свойства. На основании полученных знаний ученики в первую очередь должны овладеть приемом прибавления одинозначных чисел с переходом через десяток, то есть табличный случай прибавления с переходом через десяток(9+3), а позже и другие приемы.

Изучению табличных случав прибавления надо уделять особое внимание, потому что здесь ученики должны не только усвоить прием, но и запомнить табличные результаты.

Чтобы подготовить детей к ознакомлению с новым случаем сложения, надо рассмотреть с ними прием сложения однозначных чисел к 10. Учитель объясняет, что дополнить число, например 6, к 10 - значит подобрать другое число, которое надо прибавить до 6, чтобы достать 10. Потом решают упражнения на дополнение чисел до 10.

Кроме ознакомления с приемом прибавления, решают удобным способом примеры вида : 5(5+4), 8(6+2) и т. д. Ученики объясняют, что здесь удобнее прибавить сначала то слагаемое, какой дополняет первое число к 10, потому что к числу 10 легко прибавить второе слагаемое.

При ознакомлении с приемом можно использовать специальное наборное полотно с двумя десятками карманов, размещенных двумя рядами, и двумя десятками двухцветных кружков, которые вставляют в кармашки (рис. 17).

Иллюстрируя , наприклад, прийом для случая 9+3, в один ряд вставляємо 9 кружков одного кольору, потом выясняем, скольки кружков еще можна вставити в цей ряд, то есть скольки знадо добавить к 9, щоб дополнить до 10, и сколько нужно еще прибавить….. Один кружок другого цвета вставляем в первуй ряд, а два таких самих кружка в другой ряд. Учитель объясняет, що тут число 3 заменили сумою удобных слагаемых 1 и 2. Дети объяняют, почему эти слагаемые удобнее

Одновременно записывают:

9 + 3 = 9 + (1 + 2) = (9 + 1) + 2 =. 12.

Аналогично рассматривают на этом же уроке иные случаи: 8+6, 7+5 и т. д. Решая примеры, ученики самостоятельно делают розгор-нутий запись и дают соответствующие объяснения, например:

7+5. Заменю число 5 сумою удобных слагаемых 3 і 2; получили например: к числу 7 прибавить сумму чисел 3 и 2; удобнее прибавить к 7 число 3, первое слагаемое 7 второе 3 , и к полученному результату, 10, прибавить 2, Второе слагаемое будет 2 сумма чисел равна 12.

Табличные результаты надо запоминать постепенно. Сначала заучивают случаи одинаковых слагаемых : 6+6, 7+7, 8+8, 9+9. Здесь полезно показать, как, пользуясь результатами этих случаев, найти результаты в примерах вида : 6+5, 6+7; 7+8 и т. д. (прибавили на единицу больше или меньше и достанем на единицу больше или меньше).

В заключение сосавляют таблицу всех случаев сложения с переходом через десяток:

9 + 2=11 8 + 3=11 7 + 4 = 11 6 + 5=11

9 + 3=12 8 + 4=12 7 + 5 =12 6 + 6=12

9 + 4=13 8 + 5=13 7 + 6=13

9 + 5=14 8 + 6=14 7 + 7 = 14

9 + 6=15 8 + 7=15

9 + 7=16 8 + 8=16
9 + 8= 17
9 + 9= 18

Пусть ученики проследят, как можно достать в каждом столбике следующий результат из предыдущего, а сравнив результаты в строках, установят, что они одинаковы(9+2=11, 8+3=11 и т. д.). Надо обратить внимание детей на то, что каждая таблица заканчивается случаем добавления одинаковых слагаемых, и выяснить, почему не надо продолжать таблицу.

Запомнить табличные результаты помогают разные формы зав-дань, например: записать все примеры на добавление чисел из від-повіддю 11(12, 13 .., 18); записать все одинцифровые числа и збіль-шити каждое на 9(на 8, на 7) и тому подобное. Полезно применять трену-вальні упражнения в форме игр.

Чтобы подготовить учеников к приему вычитания, который основывается на знании таблицы добавления, надо давать специальные упражнения, спря-мовані на усвоение состава чисел второго десятка. Да, користую-чись составленной таблицей, ученики называют, суммой которых двух одно-цифровых чисел есть, например, число 11(12, 13 .., 18), и записывают 11=9+2, 11 = 8+3 и т. д.

Выучив свойства вычитания суммы от числа по такой же методике, как и другие свойства, рассматривают вычитание вида 12-5.

Для этого случая вычитания целесообразно рассмотреть три прийо-ми: первый основывается на использовании свойства вычитания су-ми от числа, второй- на использовании свойства вычитания числа от суммы, а третий - на знании состава чисел второго десятка и связи между результатом и компонентом действия добавления.

Подготовкой к использованию первого приема будет розв'язу-вання удобным способом примеров вида 13 -(3 + 2). При ознайом-ленні с приемом используют то же наборное полотно, какое за-стосовували, рассматривая прием добавления виду 9+5(см. рис. 17).

Предлагают развязать пример 12-5. Каждый ученик у себя на парте, а один на доске откладывают на наборном полотне 12 круж-ків. Учитель спрашивает, как удобнее отнять 5 от 12. Ученики запропону-ють отнять сначала 2#00, а потом еще 3#01. Выясняют, что число 5 замінили суммой удобных до-данків 2 и 3, отняли сначала одно слагаемое, а потом от найденного результата - второй.

Запись: 12-5=12-т = (12-2}- 3=7.

При этом ученик объясняет, исходя из рассмотренной ранее схемы: "Заменю число 5 суммой удобных слагаемых 2 и 3; приведем пример: от 12 отнять сумму чисел 2 и 3; удобнее сначала отнять 2, первое слагаемое, а от найденного результата, от 10, отнять 3, второе слагаемое, получим 7".

Не исключено, что дети самостоятельно предложат прием замены уменьшаемого суммой разрядных слагаемых :

12 - 5(10 + 2) - 5 + 2 = 7.

В этом случае после коллективного рассмотрения надо сказать ді-тям, что можно пользоваться и таким способом. Если ученики само-стійно не придут к этому способу, то учитель должен запропону-вати его, но несколько позже.

Чтобы подготовить учеников к использованию приема, какой грунту-ється на знании состава чисел второго десятка, надо повторить аналогичный прием с числами первого десятка, больше приділити внимания работе над составом чисел друрого десятка и выполнить специальные упражнения на нахождение результата вычитания за соответствующим результатом добавления(например, найти результаты второго и тре-тього примеров за результатом первого : 7+5 .12-7, 12-5). После такой подготовки ученики самостоятельно находят для случая вида 14-5 третий прием: 14 - это сумма чисел 5 и 9; если от 14 отн противопоставлении, з'ясу-вавши, чем отличаются приемы#00.

Дальше вводят в противопоставлении аналогичные случаи добавления и вычитания парами. Методический подход к раскрытию этих случаев предыдущий: сначала осуществляют подготовительную работу, потом ученики знакомятся с новыми случаями добавления и вычитания, после чего формируют навыки. Рассмотрим для остальных случаев пояснен-ня, которые должны давать ученики, и соответствующие записи. Сначала на одном уроке рассматривают случаи:

47+9. Заменим число 9 суммой удобных слагаемых 3 и 6; получим пример: к 47 прибавить сумму чисел Из и 6; удобнее до 47 прибавить Из, первое слагаемое, и к найденному результату, до 50, прибавить 6, дру-гий слагаемое, будет 56.

Запись: 47+9=47 +6=56.

47-9. Заменим число 9 суммой удобных слагаемых 7 и 2; получим пример: из 47 отнять сумму чисел 7 и 2; удобнее вот 47 отнять 7, первое слагаемое; вот найденного результата, вот 40, отнять 2, дру-гий слагаемое, будет 38.

Запись: 47-9=47 -(47-7) - 2=38.

 

Потом на одном уроке рассматривают случаи: 30+12 и 30-12.

30+12. Замінимо число 12 суммой разрядных слагаемых 10 и 2; ді-станемо пример: к ЗО прибавить сумму чисел 10 и 2; удобнее к ЗО прибавить 10, первое слагаемое, и к результату, до 40, прибавить 2, второй -доданок, будет 42.

Запись: 30+12=30+2=42.

По рассмотрении этого приема добавления можно подвести учеников к новому приему добавления двоцифрового числа к одноцифро-вого, когда есть переход через десяток.

47+9. Заменим число 47 суммой разрядных слагаемых 40 и 7; получим пример: к сумме чисел 40 и 7 прибавить 9; удобнее прибавить 9 до 7, ко второму слагаемому , и результат(16) прибавить к 40, к первому слагаемому, будет 56.

Запись: 47+9 +9=40 =56.

30-12. Заменю число 12 суммой разрядных слагаемых 10 и 2; получим пример: от ЗО отнять сумму чисел 10 и 2; удобнее от ЗО отнять 10, первое слагаемое, а от результата, от 20, отнять 2, второе слагаемое, будет 18.

Запись: 30-12=30 -(30-10) - 2= 18.

Потом рассматривают одновременно случаи: 65+14 и 65-14 и, наконец, также одновременно случаи с переходом через десяток: 36+19 и 36-19. Наведем для них развернутую запись объяснения :

65 + 14 = 65 + 4 = 79 65 - 14 = 65 -(65 - 10) - 4 = 51 36 + 19 = 36 + 9 = 55 36-19 = 36 -(36-10) - 9= 17 Для этих случаев, как и для предыдущих, ученики самостоятельно знахо-дять приемы вычислений и дают соответствующие объяснения.

Для двух последних случаев ученики обычно предлагают другие приеми: заменяют суммой разрядных слагаемых не только первый компонент, но и второй или заменяют один из компонентов суммой удобных слагаемых. Например, для случая 36+19 ученики находят такие приеми:

36 + 19 = ЗО + 6 + 19 = ЗО + 19 + 6 = 55 36 + 19 - =36 + 4 + 15 = 36 + 4 + 15 = 55 36 + 19 = 35 + 1 + 19 = 35 + 1 + 19 = 55 и т. д.

В II классе после изучения свойств прибавления сумми к сумме и вычитанию суммы из суммы и вводят приемы поразрядного прибавления и вычитания двузначных чисел.

До сих пор ученики так овладевают общим приемом использования влас-тивостей для обоснования вычислительных приемов, которые могут самостоятельно найти новые приемы. Потом, решая примеры, во-ни так записывают объяснение:

65 + 14 = 60 + 5 + 10 + 4 = 60 + 10 + 5 + 4 = 79 65 - 14 = 60 + 5 - 10 + 4 = 60 - 10 + 5 - 4 = 51

Одновременно объясняют: замінюючи каждое число суммой розряд-них слагаемых, достанем пример: к сумме чисел 60 и 5 прибавить сумму чисел Ш и 4; удобнее прибавить первые слагаемые 60 и 10, потом вторые до-данки 5 и 4, прибавив результаты, достанем 79.

В II классе надо в течение всего учебного года приділяти значительное внимание формированию навыков добавления и вычитания чисел в пределах 100, решая для этого разные упражнения на вычисление(зна-ходження значений выражений, заполнения таблиц и тому подобное).