Особенности расчета поля в дальней зоне антенны

Выражения (1), (5) для результирующего поля на первый взгляд просты; однако при произвольном положении точки наблюдения процесс интегрирования или суммирования не позволяет получать простых замкнутых выражений, допускающих наглядную трактовку. Сложность эта связана прежде всего с тем, что поле каждо­го излучающего элемента известно в своей собственной системе коор­динат, связанной с самим излучателем. Для нахождения результирую­щего поля необходимо ввести единую для всех элементов систему ко­ординат и выразить поля всех элементов в этой общей системе коор­динат.

Наибольший практический интерес при излучении антенны пред­ставляет электромагнитное поле, создаваемое на большом расстоянии от нее (так называемая дальняя зона антенны или зона Фраунгофера. Сформулировать суть упрощений, допускаемых при расчете поля на большом расстоянии, а также оценить это расстояние можно следу­ющим образом.

Рассмотрим систему из дискретных излучателей, одинаково ори­ентированных в пространстве, а именно так, что любой излучающий элемент может быть совмещен с другим только путем параллельного перемещения в пространстве без вращения. Введем общую прямоу­гольную систему координат x, у, z, центр которой расположим внутри излучающей системы. Выделим произвольный элемент с номером n (рис. 3), находящийся на расстоянии p_n от начала общей системы координат. Оси локальной системы координат х_n, у_n, z_n ориентируем параллельно соответствующим осям системы координат х, у, z. Вве­дем также общую сферическую систему координат r, Θ, φ. В системе координат r_n, Θ_n, φ_n каждая компонента поля излучения рассматривае­мого элемента имеет вид (индексы, соответствующие различным ком­понентам, опущены)

 

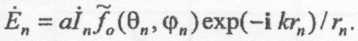(6)

 

Необходимо все функции, входящие в (6) и зависящие от ко­ординат r_n, Θ_n, φ_n выразить через r, Θ, φ. С особой осторожностью сле­дует подойти к замене r_n на r в фазовом множителе, поскольку даже небольшое отличие r_n от r может привести к большим фазовым ошибкам. Так, если р_n составляет всего 15 мм, то на частоте f = 10 ГГц максимальная фазовая ошибка при замене r_n на r независимо от абсолютного значения r может составить ∆Ф = 180°. Расстояние r_n , характеризующее положение точки наблюдения М в локальной системе координат, можно определить по формуле

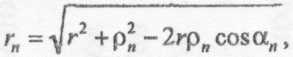(7)

 

где α_n - угол между вектором r и p - вектором, направленным из начала общей системы координат в точку расположения n-го элемента (см. рис. 3, а).

В дальней зоне излучающей системы можно ограничиться пер­выми двумя членами ряда, т.е. положить

(8)

Указанное равенство равносильно тому, что лучи, проведенные в точку наблюдения М из начала общей системы координат и из точки расположения излучаемого элемента, считаются па раллельными (см. рис. 3, б). Величина p_ncoscα_n = ∆r_n носит название разности хода лу­чей. Из параллельности лучей сразу следует равенство угловых координат: Θ_n = Θ, φ_n= φ. Следовательно, векторы Е, создаваемые отдель­ными излучателями в точке наблюдения, параллельны между собой; компоненты результирующего вектора можно находить как сумму компонент каждого из элементарных полей; для каждой из компонент поля можно вынести из-под знака суммы функцию, соответствующую ком­плексной ДН.

 

 

Рис. 3 – Графическая интерпретация для определения расстояния r_n

 

Естественно, что принятые выше допущения тем строже, чем больше расстояние r. Определим более точно, при каком расстоянии можно ими пользоваться. Основная погрешность определяется третьим слагаемым при определении r_n. Отбрасывание этого слагаемого дает ошибку при вы­числении фазового множителя. Если потребовать, чтобы фазовая ошибка не превыша­ла π/8, т.е. 22,5°, то необходимо, чтобы

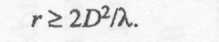(9)

Из (9) следует, что с увеличением размеров излучающей сис­темы граница дальней зоны резко отодвигается от антенны. Так, если D = 10λ, то дальняя зона начинается с r = 200λ. При частоте f=10 ГГц это расстояние составит 6 м. При D = 100λ граница дальней зоны начинается с расстояния r = 20000λ, что соответствует 600 м.

Отметим еще раз, что условие (9) дает верхнюю границу даль­ней зоны во всем секторе углового положения точек наблюдения отно­сительно антенны, поскольку оно справедливо для углов α_n, близких к π/2. При значениях α_n, близких к нулю, требования к расстоянию r, значительно ослаб­ляются, т.е. граница дальней зоны в этих направлениях приближается к антенне и определяется, по существу, уже не фазовыми ошибками при суммировании (5), а амплитудными погрешностями, обусловленны­ми отличием r_n от r. Таким образом, при заданной геометрии антенны граница дальней зоны зависит от углового положения точек наблюдения.

Обычно расстояние между передающей антенной и точкой при­ема существенно больше, чем это требуется формулой (9), однако знание границы дальней зоны важно при экспериментальном иссле­довании характеристик антенн, в частности при измерении ДН.

При этом каждую компоненту результирующего поля можно вычислить как

 

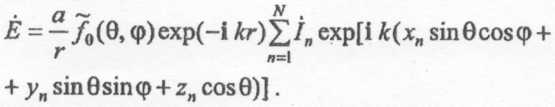(10)

 

Описанные выше излучающие системы из идентичных элемен­тов носят название антенных решеток (АР) и широко применяются в антенной технике для увеличения направленности излучения. Из вы­ражения (10) видно, что для АР диаграмма направленности всей из­лучающей системы, т.е. зависимость напряженности поля от угловых координат, определяется для каждой из компонент выражением, приведенным в справочнике.

Подчеркнем, что множитель системы для любой антенной решетки из элементов, идентично расположенных в пространстве, определяется тремя факторами: амплитудой токов в элементах, фазами токами в элементах и фазовым сдвигом между полями, обуcловленными разностью хода лучей от каждого элемента по сравнению с лучом, проведенным в точку наблюдения из начала общей системы координат.

Расчет поля в области промежуточной и ближней зон существен­но сложнее, чем в дальней зоне, ввиду невозможности использования принятых выше допущений. Основное отличие структуры поля в про­межуточной зоне от поля в дальней зоне проявляется в том , что на монотонное убывание поля по закону 1/rнакладывается осциллирую­щее амплитудное затухание, а угловая зависимость поля оказывается зависящей от r, те. ДН в промежуточной зоне искажается. В ближней зоне поля имеют как поперечные, так и продольные составляющие, зависимость от расстояния rносит здесь нерегулярный характер. Не­обходимость знания поля в промежуточной и ближней зонах связана с расчетом входного сопротивления антенн, эффектов взаимной связи между близко расположенными антеннами (проблема электромагнит­ной совместимости (ЭМС)), влияния поля антенны на обслуживаю­щий персонал. Кроме того, знание структуры поля в ближней или про­межуточной зоне позволяет путем соответствующего пересчета опре­делять ДН антенны в дальней зоне. Это используется на практике для больших антенн, у которых размеры дальней зоны чрезмерно велики [см. формулу (9)], что затрудняет непосредственное измерение ДН в дальней зоне.