Диференціальне числення функції багатьох змінних.

Функція – функція двох змінних і . Областю визначення функції є деяка множина точок площини ( може бути вся площина, або частина площини, обмежена певними лініями ). Існують частинні похідні функції першого порядку по : та по : . При знаходженні похідної по певній змінній всі інші змінні вважаємо сталими. Правила диференціювання і таблиця похідних такі ж самі, як для функції однієї змінної. Частинні похідні першого порядку є функціями двох змінних. Їх можна диференціювати. Дістанемо другі частинні похідні: , , . При цьому , тобто .

Повний диференціал функції обчислюється за формулою:

Похідна складеної функції: а) функція залежить від двох змінних та , кожна з яких, в свою чергу, є функцією змінної : , , тоді ;

б) маємо функцію , де , тоді ;

в) маємо функцію , де , , тоді і .

Функція є неявно заданою, якщо рівняння не може бути розв’язане відносно . Тоді частинні похідні цієї функції визначаються формулами:

і .

Нехай задано поверхню . Точка належить цій поверхні і функція диференційована в ній. Рівняння дотичної площини, яка проходить через точку , має вигляд: . Рівняння нормалі, яка проходить через точку , має вигляд: Якщо рівняння поверхні задано в явній формі , то поклавши , можна застосувати наведені вище формули.

Якщо функція має екстремум в точці , то в цій точці частинні похідні першого порядку по змінних та дорівнюють нулю або не існують. Точка, що задовольняє цим умовам, називається критичною, наприклад, . Вона буде екстремальною, якщо

. Якщо , то точка не экстремальна. У випадку, коли , необхідне додаткове дослідження.

Задача 25. Знайти і побудувати область визначення функції:

Розв’язання: Функція визначена при , або . Функція існує, якщо , тобто у двох випадках:

при і при . Звідки область визначення всієї функції:

 

і

 

Побудуємо область визначення функції.

 

 

 

Задача 26. Знайти частинні похідні першого порядку для функції

Розв’язання: При знаходженні похідної по певній змінній всі інші змінні вважаємо сталими.

Задача 27. Довести, що функція задовольняє заданому рівнянню.

Розв’язання:

Підставимо знайдені похідні в рівняння:

Задача 28. Знайти перші частинні похідні неявно заданої функції

Розв’язання: Маємо , де

. Знайдемо похідні

,

,

.

,

.

Задача 29.Знайти перші похідні складної функції.

Розв’язання: Знайдемо похідні:

,

, .

Маємо:

Задача 30. Знайти повний диференціал функції:

Розв’язання: Знайдемо перші частинні похідні: . Тоді

Задача 31.Скласти рівняння дотичної площини і нормалі до поверхні в точці .

Розв’язання: Запишемо рівняння площини в неявному вигляді:

. Знайдемо частинні похідні в точці М₀

; ;

Підставимо в рівняння дотичної площини знайдені значення. Матимемо: або

і відповідно рівняння нормалі:

.

Задача 32. Дослідити на екстремум функцію:

Розв’язання: Область визначення функції – вся числова площина . Обчислимо частинні похідні функції:

. Знайдемо критичні точки. Розв’яжемо систему: .

Розв’язком будуть дві точки і . Обидві точки належать області визначення. Обчислимо частинні похідні другого порядку даної функції: . Знайдемо їх значення в точках і : , , і , , . Покладемо .

В точці : . Отже, екстремуму немає. В точці : . Отже, екстремум є. Так як , то в точці функція має мінімум. Мінімум функції

.

1.2 Індивідуальні завдання

Завдання 1.Розв’язати матричне рівняння.

 

1.		2.
3.		4.
5.		6.
7.		8.
9.		10.
11.		12.
13.		14.
15.		16.
17.		18.
19.		20.
21.		22.
23.		24.
25.		26.
27.		28.
29.		30.

Завдання 2. Розв’язати систему ЛАР трьома способами: а) по формулам Крамера; б) матричним методом; в) методом Гаусса.

 

1.		2.
3.		4.
5.		6.
7.		8.
9.		10.
11.		12.
13.		14.
15.		16.
17.		18.
19.		20.
21.		22.
23.		24.
25.		26.
27.		28.
29.		30.

Завдання 3. Задані координати вершин піраміди . Знайти: а) Кут між ребрами та ; б) Площу грані ; в) Проекцію вектора на вектор , г) Довжину висоти піраміди, проведену з вершини , д) Яку трійку утворюють вектори , і ?

 

1.	А1( 2; 1; 4 )	А2( -1; 5; -2 )	А3 (-7; -3; 2 )	А4( -6; -3; 6 )
2.	А1( 5; 2; 0 )	А2( 2; 5; 0 )	А3( 1; 2; 4 )	А4( -1; 1; 1 )
3.	А1( 1; 2; 0 )	А2 (3; 0; -3 )	А3( 5; 2; 6 )	А4( 8; 4; -9 )
4.	А1( 2; -1; 2 )	А2( 1; 2; -1 )	А3( 3; 2; 1 )	А4( -4; 2; 5 )
5.	А1( 1; 1; 2 )	А2( -1; 1; 3 )	А3( 2; -2; 4 )	А4( -1; 0; -2 )
6.	А1( 2; 3; 1 )	А2( 4; 1; -2 )	А3( 6; 3; 7 )	А4( 7; 5; 3 )
7.	А1( 1; 5; -7 )	А2( -3; 6; 3 )	А3( -2; 7; 3 )	А4( -4; 8; -12)
8.	А1( 0; -1; -1 )	А2( -2; 3; 5 )	А3( 1; -5; -9 )	А4( -1; -6; 3 )
9.	А1( 7; 2; 4 )	А2( 7; -1; -2 )	А3( 3; 3; 1 )	А4( -4; 2; 1 )
10.	А1( 4; -1; 3 )	А2( -2; 1; 0 )	А3( 0; -5; 1 )	А4( 3; 2; -6 )
11.	А1( 2; 0; 0 )	А2( -2; 0; -1 )	А3( 1; 4; 2 )	А4( 3; 0; 6 )
12.	А1( -2; 0; 2 )	А2( 0; 0; 4 )	А3( 3; 2; 4 )	А4( 1; 3; 2 )
13.	А1( 1; 2; 3 )	А2( 2; 0; 0 )	А3( 3; 2; 5 )	А4( 4; 0; 0 )
14.	А1( 3; 0; 6 )	А2( 1; -3; 2 )	А3( 3; 2; 5 )	А4( 2; 2; 5 )
15.	А1( -2; 0; -1 )	А2( 0; 0; 4 )	А3( 1; 3; 2 )	А4( 3; 2; 7 )
16.	А1( 1; -2; 1 )	А2( 0; 0; 4 )	А3( 1; 4; 2 )	А4( 2; 0; 0 )
17.	А1( -2; 1; 0 )	А2( 3; 2; 7 )	А3( 2; 2; 5 )	А4( 6; 1; 5 )
18.	А1( -1; 3; 0 )	А2( 2; 0; 0 )	А3( 4; -1; 2 )	А4( 3; 2; 7 )
19.	А1( 6; 1; 5 )	А2( 5; 1; 2 )	А3( -4; 1; -2 )	А4( -6; 0; 5 )
20.	А1 (1; -1; 6 )	А2( -5; -1; 0 )	А3( 4; 0; 0 )	А4( 2; 2; 5 )
21.	А1( 4; 2; 5 )	А2( 0; 7; 2 )	А3 (0; 2; 7 )	А4( 1; 5; 0 )
22.	А1( 4; 4; 10 )	А2( 4; 10; 2 )	А3( 2; 8; 4 )	А4( 9; 6; 9 )
23.	А1( 4; 6; 5 )	А2( 6; 9; 7 )	А3( 2; 10; 10 )	А4( 7; 5; 9 )
24.	А1( 3; 5;4 )	А2( 8; 7; 4 )	А3 ( 5; 10; 4 )	А4( 4; 7; 8 )
25.	А1( 10; 6; 6 )	А2( -2; 8; 2 )	А3( 6; 8; 9 )	А4( 7; 10; 3 )
26.	А1( 1; 8; 2 )	А2( 5; 2; 6 )	А3( 5; 7; 4 )	А4( 4; 10; 9 )
27.	А1( 6; 6; 5 )	А2( 4; 9; 5 )	А3( 4; 6; 11 )	А4( 6; 9; 3 )
28.	А1( 7; 2; 2 )	А2( 5; 7; 7 )	А3( 5; 3; 1 )	А4( 2; 3; 7 )
29.	А1( 8; 6; 4 )	А2( 10; 5; 5 )	А3( 5; 6; 8 )	А4( 8; 10; 7 )
30.	А1( 7; 7; 3 )	А2( 6; 5; 8 )	А3( 3; 5; 8 )	А4( 8; 4; 1 )

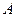Завдання 4. Дані вершини трикутника . Знайти а) довжину та рівняння сторони ; б) довжину та рівняння висоти, проведеної до сторони , в) рівняння середньої лінії, яка з’єднує сторони та , г) кут при вершині . Зробити рисунок трикутника.

 

1.	А ( 2, - 3 )	В ( 3, 0 )	С ( - 2, 5 )
2.	А ( 1, 3 )	В ( - 1, 0 )	С ( 2, - 2 )
3.	А ( 1, 2 )	В (- 1, - 1 )	С ( 2, 1 )
4..	А ( 2, 1 )	В ( 4, 3 )	С ( - 2, 1 )
5.	А ( 1, - 1 )	В ( 6, 4 )	С ( 2, 6 )
6.	А ( 2, - 3 )	В ( 3, 2 )	С ( - 2, 5 )
7.	А ( 3, 2 )	В ( 5, - 2 )	С ( 1, 3 )
8.	А ( 3, - 4 )	В ( - 2, 3 )	С ( 4, 5 )
9.	А ( 3, 6 )	В ( - 1, 3 )	С ( 2, - 1 )
10.	А ( 5, - 4 )	В ( - 1, 3 )	С ( - 3, - 2 )
11.	А ( 1, 1 )	В ( 7, 4 )	С ( 4, 5 )
12.	А ( 1, 1 )	В ( - 5, 4 )	С ( - 2, 5 )
13.	А ( - 1, 1 )	В ( 5, 4 )	С ( 2, 5 )
14.	А ( - 1, 1 )	В ( - 7, 4 )	С ( - 4, 5 )
15.	А ( 1, - 1 )	В ( 7, 2 )	С ( 4, 5 )
16.	А ( 1, - 1 )	В ( -5, 2 )	С ( - 2, 3 )
17.	А ( -1, -1 )	В ( 5, 2 )	С ( 2, 3 )
18.	А ( - 1, - 1 )	В ( - 7, 2 )	С ( - 4, 3 )
19.	А ( 0, 1 )	В ( 6, 4 )	С ( 3, 5 )
20.	А ( 1, 0 )	В ( 7, 3 )	С ( 4, 4 )
21.	А ( 2, - 3 )	В ( - 3, 0 )	С ( 2, 5 )
22.	А ( 1, 3 )	В ( 2, 0 )	С ( - 2, - 2 )
	А ( 1, 2 )	В ( 2, - 1 )	С ( - 3, 1 )
24.	А ( 2, 1 )	В ( - 4, 3 )	С ( 1, 1 )
25.	А ( 1, - 1 )	В ( - 3, 4 )	С ( - 2, 6 )
26.	А ( 2, - 3 )	В ( - 3, 2 )	С ( 2, 5 )
27.	А ( 3, 2 )	В ( - 3, - 2 )	С ( - 2, 3 )
28.	А ( 3, - 4 )	В ( 4, 3 )	С ( - 1, 5 )
29.	А ( 3, 6 )	В ( 2, 3 )	С ( - 3, 1 )
30.	А ( 5, - 4 )	В ( 4, 3 )	С ( 2, - 2 )

Завдання 5. Дано точки: , , , . Знайти: а) рівняння прямої, яка проходить через т. паралельно прямій ; б) рівняння площини ; в) рівняння прямої, яка проходить через т. перпендикулярно площині .

 

1.	А( 0; -1; 2 )	B( 2;-2; 2 )	С( -1;-1 ; 3 )	D( 2;-1; 3 )
2.	А( 2; -1; 3 )	В( 1; -4; 4 )	С( 4; -2; 3 )	D( -1;2 ; 3 )
3.	А( -1; 2; 3 )	В( -2; 2; 4 )	С( 1; 1; 3 )	D( -1;3 ; 2 )
4.	А( -1;3 ; 2 )	В ( -2; 3 ; 3 )	С( 1; 2; 2 )	D( 2; 3;-1 )
5.	А( 2; 3;-1 )	В( 1; 3;0 )	С( 4; 2; -1 )	D( 0; 4; -1 )
6.	А( 0; 2;-1 )	В( -1; 2;0 )	С( 2;1 ; -1 )	D( -2; 0;1 )
7.	А( -2; 0; 1 )	В( -3;0 ;2 )	С( 0;-1 ; 1 )	D( 1;0 ;-2 )
8.	А( 1; 0; -2 )	В( 0; 0; -1 )	С( 3;-1 ; -2 )	D( 0; 1 ; -2 )
9.	А( 0; 1; -2 )	В( -1; 1; -1 )	С( 2; 0 ;-2 )	D( -2; 1 ; 0 )
10.	А( -2;1 ;0 )	В( -3; 1; 1 )	С( 0; 0; 0 )	D( -2; -1; 0 )
11.	А( -2; -1;0 )	В( -3; -1; 1 )	С( 0; -2; 0 )	D( 0; -2; -1 )
12.	А( 0; -2; -1 )	В( -1; -2; 0 )	С( 2; -3; -1 )	D( -1; 0; -2 )
13.	А( -1; 0 ;-2 )	В( -2; 0; -1 )	С( 1; -1; -2 )	D( 0; -1; -2 )
14.	А( 0; -1;-2 )	В( -1; -1; 1 )	С( 2; -2; -2 )	D( -2; 0; -1 )
15.	А( -2; 0; -1 )	В( -3; 0; 0 )	С( 0; -1; -1 )	D( -1; -2; 0 )
16.	А( 0; -1; 2 )	В(-1; -1; 3 )	С( 2; -2; 2 )	D( 2;-1; 3 )
17.	А( 2; -1; 3 )	В( 4; -2; 3 )	С( 1; -1; 4 )	D( -1; 2; 3 )
18.	А( -1; 2; 3 )	В (1; 1; 3 )	С( -2; 2; 4 )	D( -1; 3; 2 )
19.	А( -1; 3; 2 )	В( 1; 2; 2 )	С( -2; 3; 3 )	D( 2; 3; -1 )
20.	А( 2; 3; - 1)	В( 4; 2; -1 )	С( 1; 3; 0 )	D( 0 ;2; -1 )
21.	А( 0; 2; -1 )	В( 2; 1; -1 )	С( -1; 2; 0 )	D( -2; 0; 1 )
22.	А( -2; 0; 1 )	В( 0; -1; 1 )	С( -3; 0; 2 )	D( 1; 0; -2 )
23.	А( 1; 0; -2 )	В( 3; -1; -2 )	С( 0; 0; -1 )	D( 0; 1; -2 )
24.	А( 0; 1;-2 )	В( 2; 0; -2 )	С( -1; 1; -1 )	D( -2; -1; 0 )
25.	А( -2; 1; 0 )	В( 0; 0; 0 )	С( -3; 1; 1 )	D( -2; -1; 0 )
26.	А( -2; -1; 0 )	В( 0; -2; 0 )	С( -3; -1; 1 )	D( 0; -2; -1 )
27.	А( 0; -2; -1 )	В( 2; -3; -1 )	С( -1; -2; 0 )	D( -1; 0; -2 )
28.	А( -1; 0; -2 )	В( 1; -1; -2 )	С( -2; 0; -1 )	D( 0; -1; -2 )
29.	А( 0; -1; -2 )	В( 2; -2; -2 )	С( -1; -1; -1 )	D( -2; 0; -1 )
30.	А( -2; 0; -1 )	В( 0; -1; -1 )	С( -3; 0; 0 )	D( -1; -2; 0 )

Завдання 6. Знайти границі функції

 

1.	а)
	б)		в)
	г)
2.	а)
	б)		в)
	г)
3.	а)
	б)		в)
	г)
4.	а)
	б)		в)
	г)
5.	а)
	б)		в)
	г)
6.	а)
	б)		в)
	г)
7.	а)
	б)		в)
	г)
8.	а)
	б)		в)
	г)
9.	а)
	б)		в)
	г)
10.	а)
	б)		в)
	г)
11.	а)
	б)		в)
	г)
12.	а)
	б)		в)
	г)
13.	а)
	б)		в)
	г)
14.	а)
	б)		в)
	г)
15.	а)
	б)		в)
	г)
16.	а)
	б)		в)
	г)
17.	а)
	б)		в)
	г)
18.	а)
	б)		в)
	г)
19.	а)
	б)		в)
	г)
20.	а)
	б)		в)
	г)
21.	а)
	б)		в)
	г)
22.	а)
	б)		в)
	г)
23.	а)
	б)		в)
	г)
24.	а)
	б)		в)
	г)
25.	а)
	б)		в)
	г)
26.	а)
	б)		в)
	г)
27.	а)
	б)		в)
	г)
28.	а)
	б)		в)
	г)
29.	а)
	б)		в)
	г)
30.	а)
	б)		в)
	г)

Завдання 7. Дослідити на неперервність функцію, встановити характер точок розриву, якщо вони існують. Зробити схематичне креслення: