Пересечение конуса проецирующей плоскостью

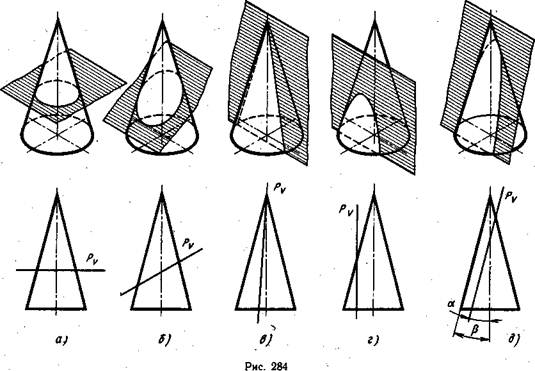
На рис. 284 показаны примеры пересечения конуса плоскостями различного положения, где каждому наглядному изображению соответст­вует фронтальная проекция конуса со следом секущей плоскости.

Если Прямой круговой конус рассечь плоско­стью, параллельной основанию, то линия пере­сечения боковой поверхности конуса с плоско­стью будет окружностью (рис. 284, а).

Если конус рассечь наклонной плоскостью так, чтобы пересеклись все его образующие, то линия пересечения боковой поверхности конуса с плоскостью будет эллипсом (рис. 284, б).

Если конус рассечь плоскостью, проходящей через его вершину, то, будет ли плоскость пер­пендикулярна или наклонна к основанию, линия пересечения боковой поверхности конуса с пло­скостью будет треугольником (рис. 284, в).

Если на поверхности конуса можно провести две образующие параллельно пересекающей его плоскости, то такая плоскость пересечет боко­вую поверхность конуса по гиперболе (рис. 284, г).

Если плоскость пересекает конус параллельно одной образующей, то боковая поверхность конуса пересечется этой плоскостью по парабо­ле (рис. 284, д). При таком положении пло­скости, пересекающей конус, угол а между ее следом и осью конуса равен углу р между осью и образующей конуса. Если α>β, то в пересече­нии получится эллипс, а если α<β, то в пересе­чении получится гипербола. Гипербола получит­ся и тогда, когда α=0, т. е. секущая плоскость параллельна оси конуса.