б) Найдите угол между этой плоскостью и плоскостью основания.

Решение.

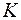а) Возьмем на ребре произвольно точку . Из нее в плоскости грани проводим прямую , образующую угол с ребром 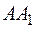, до пересечения с продолжением стороны 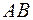в точке . Очевидно, что .

Из точки 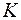в плоскости грани проводим прямую , образующую угол с ребром 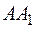,(возможны два положения прямой) до пересечения с продолжением стороны в точке .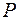

Очевидно, что (Рис. 1). Сечение - искомое.

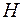б) Из точки опустим перпендикуляр на прямую и соединим точку и 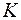. По теореме, обратной теореме о трех перпендикулярах, получим, что .

Следовательно, искомый угол.

Из прямоугольного имеем: .

Обозначим . Тогда , .

. .

. . .

Ответ: . Другой ответ:

Пример 4.

Плоскость пересекает боковые ребра и треугольной пирамиды в точках и соответственно и делит объем пирамиды пополам.

а) Постройте сечение пирамиды плоскостью, если , .

б) В каком отношении эта плоскость делит медиану грани ?

Решение.

Пусть - проекция ребра на плоскость . Из подобия и :

, - отношение высот и пирамид и .

По условию , , , , .

Значит, точка 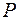делит ребро в отношении .

Сечение - искомое.

 

Обозначим: , , .

Система уравнений:

.

.

Ответ: считая от основания.

 

Пример.

Найти расстояние между серединами не смежных ребер в правильной треугольной пирамиде, все ребра которой равны 1.

Решение.

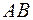Пусть - середины не смежных ребер и .

Пусть , .

, , .

Ответ: