ПРИКЛАДНАЯ МАТЕМАТИКА

МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ

 

Пермь 2012
I. Общие методические указания

Преподавание дисциплины "Прикладная математика" обосно­вывается на необходимости изучения арсенала математических методов и моделей для применения их в решении практических задач в различных сферах коммерческой и финансовой деятельности, позволяющие получить более выгодные, оптимальные решения в сравнении с традиционными приемами, привить навыки самостоя­тельного изучения литературы по математическим методам реше­ния коммерческих задач, развить логическое мышление, повысить уровень математической культуры, выработать навыки математиче­ского исследования проблем и задач финансовой и коммерческой деятельности.

Курс изучается по программе "Прикладная математика", утвержденной в 1992 г.

Цель настоящих методических указаний: оказать помощь студентам в изучении разделов и тем курса "Прикладная математика" для развития навыков по применению различных математических методов и моделей в решении практических задач коммерческой деятельности, а также подготовить к самостоятельному изу­чению литературы по математическим методам в экономике и применения их к решению новых проблем и задач в финансовой и коммерческой сферах.

Для выполнения контрольной работы студенту необходимо ознакомится с программой курса "Прикладная математика", с мето­дическими указаниями и контрольными заданиями. При изучении студент должен пользоваться рекомендуемой литературой, материалами устных и письменных консультаций, закрепляя усвоение каждой темы решением практических задач.

Студент, завершивший самостоятельное изучение дисциплины, должен выполнить две контрольные работы и сдать экзамен.

 

IV.МЕТОДИЧЕСКИЕ УКАЗАНИЯ К РЕШЕНИЮ ЗАДАЧ

1. Графический метод решения задач линейного программирования

Общей задачей линейного программирования ОЗЛП называется задача, которая состоит в определении максимального (минимального) значения линейной целевой функции:

 

 

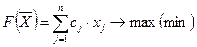
При условиях-ограничениях

 

где 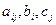-заданные постоянные величины и .

Стандартной (или симметричной) задачей линейного программирования называется задача, которая состоит в определении максимального (минимального) значения целевой функции при выполнении условий 1 и 3 , где и .

Канонической (или основной) задачей линейного программирования называется задача, которая состоит в определении максимального (минимального) значения целевой функции при выполнении условий 2 и 4, где и .

Совокупность чисел = 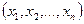удовлетворяющих ограничениям задачи, называется допустимым решением (или планом).

План = 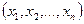, при котором целевая функция задачи принимает максимальное (минимальное) значение, называется оптимальным.

В случае, когда требуется найти минимум функции можно перейти к нахождению максимума функции , так как min .

Ограничение-неравенство исходной задачи линейного программирования, имеющее вид " ", преобразуется в ограничение-равенство добавлением к левой части дополнительных неотрица­тельной переменной, а ограничение неравенство вида " " - в огра­ничение-равенство вычитанием из левой части дополнительной неотрицательной переменной.

 

Допустим ограничения задачи отображают наличие производственных ресурсов, тогда числовое значение дополнительной переменной в плане задачи, записанной в форме основной, равно объе­му неиспользуемого соответствующего ресурса.

План называется опорным планом основной задачи линейного программирования, если система векторов, входящих в разложение с положительными коэффициентами линейно независима.

Так как векторы являются m-мерными, то из определения опорного плана следует, что число его положительных компонент не может превышать m.

Опорный план называется невырожденным, если он содержит ровно m положительных компонент, в противном случае - план вырожденный.

Свойства основной задачи линейного программирования связаны со свойствами выпуклых множеств.

Множество точек называется выпуклым, если оно вместе с любыми двумя точками содержит и их произвольную выпуклую линейную комбинацию.

Геометрический смысл этого определения состоит в том, что множеству вместе с его двумя произвольными точками полностью принадлежит и прямолинейный отрезок, их соединяющий. Примерами выпуклых множеств являются прямолинейный отрезок, полуплоскость, круг, шар, куб, полупространство и др.

Угловыми точками выпуклого множества называются точки, не являющиеся выпуклой комбинацией двух произвольных точек множества. Например, угловыми точками треугольника являются его вершины, круга - точки окружности, которые его ограничивают.

Множество планов основной задачи линейного программирования является выпуклым (если оно не пусто). Непустое множество планов называется многогранником решений, а всякая угловая точка многогранника решений - вершиной.

Если основная задача линейного программирования имеет оптимальный план, то максимальное значение целевая функция задачи принимает в одной из вершин многогранника решений. Если максимальное значение достигается более чем в одной вершине, то целевая функция принимает его во всякой точке, являющейся выпуклой линейной комбинацией этих вершин.

Непустое множество планов основной задачи линейного программирования образует выпуклый многогранник, каждая вершина которого определяет опорный план. Для одного из опорных планов (т.е. в одной из вершин многогранника решений) значение целевой функции является максимальным (при условии, что функция ограничена сверху на множестве планов).

Вершину многогранника решений, в которой целевая функция принимает максимальное значение, можно найти достаточно просто, если задача в стандартной форме содержит не более двух переменных:

при условиях

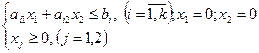
Каждое из неравенств системы ограничений задачи геометрически определяет полуплоскость допустимых значений переменных соответственно с граничными прямыми

Если система неравенств совместна, то областью допустимых решений задачи является выпуклое множество, которое называется многоугольником решений. Стороны этого многоугольника лежат на прямых, уравнения которых получаются из исходной системы ограничений заменой знаков неравенств на знаки точных равенств.

Решение задачи линейного программирования графическим методом включает следующие этапы.

1. На плоскости строят прямые, уравнения которые получаются в результате замены в ограничениях знаков неравенств на знаки точных равенств.

2. Находят полуплоскости, определяемые каждым из ограничений задачи.

3. Строят многоугольник решений.

4. Строят вектор , направление которого указывает на возрастание целевой функции.

5. Строят начальную прямую 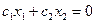и передвигают ее в направлении вектора до крайней угловой точки многоугольника решений. В результате находят точку, в которой целевая функция принимает максимальное значение, либо множество точек с одинаковым максимальным значением целевой функции, если начальная прямая сливается с одной из сторон многоугольника решений, либо устанавливают неограниченность сверху функции на множестве планов .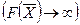

6. Определяют координаты точки максимума функции и вычисляют значение целевой функции в этой точке.

Минимальное значение линейной функции цели находится путем передвижения начальной прямой 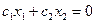, в направлении,

противоположном вектору .

Пример

Найти максимум и минимум линейной функции :

при условиях:

Решение;

Построим на плоскости многоугольник решений рис.1.

Для этого в неравенствах системы ограничений и условиях не отрицательности переменных знаки неравенств заменим на знаки точных равенств.

 

 
 

 

 


Построив полученные прямые, найдем соответствующие полуплоскости и их пересечение

 

 

Построив полученные прямые, найдем соответствующие полуплоскости и их пересечение

Многоугольником решений задачи является пятиугольник АВ-СДЕ, координаты точек которого удовлетворяют условию неотрицательности и неравенствам системы ограничений задачи.

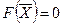Для нахождения точек экстремума построим начальную прямую и вектор . Передвигая прямую параллельно самой себе в направлении вектора , найдем точку С, в которой начальная прямая принимает положение опорной прямой. Следовательно, в точке С целевая функция принимает максимальное значение, так как точка С получена в результате пересечения прямых 1 и 2 , то ее координаты удовлетворяют уравнениям этих прямых:

Решив систему уравнений, получим:

Для нахождения минимального значения целевой функции задачи перемещаем начальную прямую в направлении, противоположном вектору . Начальная прямая займет положение опорной прямой в вершине Е. Целевая функция принимает минимальное

значение в угловой точке Е, где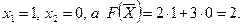

Найдем координаты угловых точек В, Д и А. Для этого решим следующие системы уравнений:

В результате получим координаты точек В (0;2,5), Д (2,0) и А (0,1).

Вычислим значения целевой функции во всех угловых точках многоугольника решений АВСДЕ:

 

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Сформулируйте общую задачу линейного программирования.

2. Дайте определение невырожденного и вырожденного опорного плана, оптимального плана.

3. Какое множество называется выпуклым?

4. Какая точка выпуклого множества называется угловой?

5. Дайте геометрическую интерпретацию задачи линейного программирования.

6. В какой точке многогранника решений целевая функция задачи линейного программирования достигает оптимального значения?

7. Какие задачи линейного программирования можно решить графическим методом?

8. Назовите особые случаи при решении задачи линейного программирования графическим методом.

2. Симплексный метод решения задачи линейного программирования.

Симплексный метод основан на последовательном переходе от одного опорного плана задачи линейного программирования к другому, при этом значение целевой функции изменяется. Рассмотрим алгоритм симплексного метода на примере задачи планирования товарооборота.

Коммерческое предприятие реализует несколько -товарных групп, располагая ограниченными материально-денежными ресурсами . Известны расходы ресурсов каждого вида на реализацию продажи единицы товарооборота товаров по каждой группе, представленной в виде матрицы и прибыль получаемая предприятием от реализации единицы товарооборота товаров группы. Определить объем и структуру товарооборота . при которых прибыль коммерческого предприятия была бы максимальной.

1. Математическую модель задачи запишем следующим образом:

Определить , который удовлетворяет ограничениям вида:

и обеспечивает максимальное значение целевой функции

 

Алгоритм симплексного метода включает следующие этапы.

2. Составление первого опорного плана.

Система ограничений задачи, решаемой симплексным методом, задана в виде системы неравенств. Перейдем от системы неравенств к системе уравнений путем введения неотрицательных дополнительных переменных. Векторы-столбцы при этих переменных представляют собой единичные векторы и образуют базис, а соответствующие им переменные называются базисными:

где базисные переменные.

свободные переменные.

Решим эту систему относительно базисных переменных:

а функцию цели перепишем в таком виде:

 

Полагая, что основные переменные

.получим первый опорный план ,(заносим его в симплексную таблицу 3, которая состоит из коэффициентов системы ограничений и свободных членов. Последняя строка таблицы называется индексной. Она заполняется коэффициентами функции цели, взятыми с противоположным знаком.

3. Проверка плана на оптимальность.

Если все коэффициенты индексной строки симплексной таблицы при решении задачи на максимум неотрицательны ( 0), то

план табл.3 задачи табл. 2 является оптимальным. Если найдется хотя бы один коэффициент индексной строки меньше нуля, то план не оптимальный и его можно улучшить. Тогда переходим к следующему этапу алгоритма.

4. Определение ведущих столбца и строки.

Из отрицательных коэффициентов индексной строки выбираем наибольший по абсолютной величине, что и определяет ведущий столбец, который показывает, какая переменная на следующей итерации перейдет из свободных в базисные.

Затем элементы столбца свободных членов симплексной таблицы делим на соответствующие только положительные элементы ведущего столбца. Результаты заносим в отдельный столбец . Строка симплексной таблицы, соответствующая минимальному значению , является ведущей. Она определяет переменную которая на следующей итерации выйдет из базиса и станет свободной.

Элемент симплексной таблицы, находящейся на пересечении ведущих столбца и строки, называют разрешающими и выделяет кружком.

5. Построение нового опорного плана

Переход к новому плану проводится пересчетом симплексной таблицы по методу Жордана-Гаусса. Сначала заменим переменные в базисе, т.е. вместо в базис войдет переменная , соответствующая направляющему столбцу.

Разделим все элементы ведущей строки предыдущей симплексной таблицы на разрешающий элемент и результаты деления занесем в строку следующей симплексной таблицы, соответствующую введенной в базис переменной . В результате этого на месте разрешающего элемента в следующей симплексной таблице будем иметь 1 , а в остальных клетках j столбца, включая клетку столбца индексной строки, записываем нули. Остальные новые элементы

нового плана находятся по правилу прямоугольника: - ,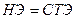

где элемент старого плана, разрешающий элемент,

А и В - элементы старого плана, образующие прямоугольник с элементам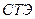и и .

 

6. Полученный новый опорный план опять проверяется на оптимальность в соответствии с этапом 3 алгоритма.

При решении задачи линейного программирования на минимум целевой функции, признаком оптимальности плана является отрицательные значения всех коэффициентов индексной строки симплексной таблицы.

Если в направляющем столбце все коэффициенты 0,то функция цели неограниченна на множестве допустимых планов, т.е. и задачу решить нельзя.

Если в столбце симплексной таблицы содержатся два или несколько одинаковых наименьших значения, то новый опорный план будет вырожденным (одна или несколько базисных переменных станут равными нулю). Вырожденные планы могут привести к зацикливанию, т.е. многократному повторению процесса вычислений, не позволяющему завершить задачу. С целью исключения этого для выбора направляющей строки используют способ Креко, который заключается в следующем. Делим элементы строк, имеющие одинаковые наименьшее значение , на предполагаемые разрешающие элементы, а результаты заносим в дополнительные строки. За ведущую строку выбирается та, в которой раньше встречается меньшее число при чтении таблицы слева направо по столбцам.

Если в оптимальный план вошла дополнительная переменная , то при реализации такого плана имеются недоиспользованные ресурсы гo вида в количестве, полученном в столбце свободных членов симплексной таблицы.

Если в индексной строке симплексной таблицы оптимального плана находится нуль, принадлежащий свободной переменной, не вошедшей в базис, а в столбце, содержащем этот нуль, имеется хотя бы один положительный элемент, то задача имеет множество оптимальных планов. Свободную переменную, соответствующую указанному столбцу, можно внести в базис, выполнив соответствующие этапы алгоритма. В результате будет получен второй оптимальный план с другим набором базисных переменных.

 

Примеры решения задачи симплексным методом

Торговое предприятие, располагающее материально-денежными ресурсами, реализует три группы товаров А, В и С. Плановые нормативы затрат ресурсов на тыс. руб. товарооборота, прибыль от продажи товаров на тыс. руб. товарооборота, а также объем ресурсов заданы в таблице 2.

Определить плановый объем продажи и структуру товарооборота так, чтобы прибыль торгового предприятия была максимальной.

 

Таблица 2

Виды материально-денежных ресурсов Норма затрат материально-денежных ресурсов на ед. товарооборота, тыс. руб. Объём ресурсов
  А _ группа _ В группа С группа  
Рабочее время продавцов, чел./ч 0,1 0,2 0,4
Площадь торговых залов, м2 0,05 0,02 0,02
Площадь складских помещений, м2
Прибыль, т.руб. max

1.Запишем математическую модель задачи.

Определить , который удовлетворяет условиям

 

и обеспечивают максимальное значение целевой функции

 

 

Для построения первого опорного плана систему неравенств, приведем к системе уравнений.

 

 

В матрице этой системы уравнений имеет:

 

 

Векторы - линейно независимы, так как определитель, составленный из компонент этих векторов, отличен от нуля:

 

Соответствующие этим векторам переменные будут базисными.

Решим систему уравнений относительно базисных переменных.

 

Функцию цели запишем в виде:

2.Полагая, что свободные переменные =0, =0, =0, получим первый опорный план

=(0,0,01100,120,8000), F = 0, в котором базисные переменные =1100, =120, =8000,

следовательно товары не продаются и прибыль равна нулю, а ресурсы не используются.

Заносим первый опорный план 1 в симплексную таблицу 3.

План Базисные переменные Ресурсы плана Значения коэффициентов при переменных
               
I план 1100 120 8000 0,1 0,05 3 0,2 0,02 1 0,4 0,02 2 0 1 0
Инд. Строка -3 -5 -4  
II план 5500 10 2500 0,5 0,04 2,5 -0,02 0 -0,1 -5
Инд. Строка -0,5  
III план 5375 250 1 875 2,25 -0,5 1,25 6,25 -2,5 1,25 -12,5 25 -62,5 0 0  
Инд. строка 5,75 23,75 12,5  

 

 

Первый опорный план 1 не оптимальный, так как в индексной строке находятся отрицательные коэффициенты - -3,-5,-4.

За ведущий столбец выберем столбец, соответствующий переменной , так как сравнивая по модулю имеем:

Рассчитываем значения 9 по строкам, как частное от деления и выбираем наименьшее:

Следовательно, первая строка является ведущей.

Разрешающий элемент равен 0,2 и находится на пересечении ведущего столбца и ведущей строки и выделен кругом.

5. Формируем следующую симплексную таблицу. Вместо переменной в план II войдет переменная . Строка, соответствующая переменной в плане II, получена в результате деления всех элементов строки плана I на разрешающий элемент . На месте разрешающего элемента в плане II получаем 1. В остальных клетках столбца плана II записываем нули.

Таким образом, в новом плане II заполнены строки и столбец . Все остальные элементы нового плана II, включая элементы индексной строки определяется по правилу прямоугольника. Для этого выбираем из старого плана 4 числа, которые расположены в вершинах прямоугольника и всегда включают разрешающий элемент . Во второй вершине по диагонали находится старое значение элемента, например, значение целевой функции , которое указывает на место расположение нового в новом плане II. Третий элемент А=1100 и четвертый элемент В=-5 завершают построение прямоугольника в недостающих двух вершинах и расположены по другой диагонали. Значение нового элемента в плане II находится из выражения:

Элементы строки определяются аналогично:

Все элементы, расположенные на пересечении строк и столбцов, соответствующих одновременным базисным элементам равны 1, остальные элементы столбца в базисах векторов, включая индексную строку, равны 0. Аналогично проводятся расчеты по всем строкам таблицы, включая индексную.

Выполняя последовательно все этапы алгоритма, формируем план II.

6.На третьей интеракции таблицы 3 получаем план III, который является оптимальным, так как все коэффициенты в индексной строке 0.

Оптимальный план можно записать так:

X = (250,5375,0,0,0,1875), 27625 тыс. руб.

Следовательно, необходимо продавать товаров первой группы А 250 ед., а второй группы В - 5375 ед. При этом торговое предприятие получает максимальную прибыль в размере 27625 тыс. руб. Товары группы С не реализуются.

"В оптимальном плане среди базисных переменных находится дополнительная переменная .Это указывает, что ресурсы третьего вида (площадь складских помещений) недоиспользована на 1875 м2 , так как переменная была введена в третье ограничение задачи, характеризующее собой использование складских помещений.

В индексной строке оптимального плана в столбцах переменных , не вошедших в состав базисных, получены ненулевые элементы, поэтому оптимальный план задачи линейного программирования является единственным.

 

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Какие задачи линейного программирования можно решать симплексным методом?

2. Каков признак оптимальности в симплексном методе?

3. Как строится первый опорный план?

4. Как определяется ведущий столбец и ведущая строка симплексной таблицы?

5. Как осуществляется пересчет элементов симплексной таблицы?

6. Каковы особые случаи при реализации симплексного метода?

 

3. ДВОЙСТВЕННАЯ ЗАДАЧА.

Двойственная задача формулируется следующим образом.

Определить оценку единицы каждого вида ресурсов, чтобы при заданных объемах ресурсов , прибыли , минимизировать оценку всех ресурсов торгового предприятия, затраченных на организацию торгового процесса.

Запишем математическую модель двойственной задачи.

Определить , который удовлетворяет ограничениям

и доставляет минимальное значение целевой функции

Ограничения показывают, что стоимость всех ресурсов, затраченных на продажу единицы группы товаров, должна быть не меньше прибыли, получаемой при реализации единицы группы товаров, а общая стоимость всех ресурсов должна быть минимизировать.

Для симметричной пары задач двойственная задача по отношению к исходной составляется согласно следующим правилам:

Число переменных в двойственной задаче равно числу ограничений в прямой задаче.

Матрица коэффициентов системы ограничений двойственной задачи получается из матрицы коэффициентов системы ограничений прямой задачи путем транспонирования.

Система ограничений двойственной задачи записывается в виде неравенств противоположного смысла неравенствам системы ограничений прямой задачи.

Свободными членами системы ограничений двойственной задачи являются коэффициенты функции цели прямой задачи.

На каждую переменную двойственной задачи накладывается условие не отрицательности. Двойственная задача решается на минимум, если целевая функция прямой задачи задается на максимум, и наоборот.

Двойственная задача решается на минимум, если целевая функция прямой задачи задаётся на максимум, и наоборот.

Коэффициентами функции цели двойственной задачи служат свободные члены системы ограничений прямой задачи.

Решение прямой задачи дает оптимальные объемы в структуру товарооборота торгового предприятия, а решение двойственной - оптимальную систему оценок ресурсов, используемых для реализации товаров.

Установим сопряженные пары переменных прямой и двойственной задач. Запишем переменные задач в двух строчках. В первой располагаем переменные по порядку номеров: сначала основные, затем -дополнительные, а во. второй строке запишем переменные двойственной задачи: сначала дополнительные, затем - основные.

основные дополнительные

дополнительные основные

Согласно сопряженным парам переменных из решения прямой задачи можно получить решение двойственной, не решая ее, и наоборот, из решения двойственной задачи можно получить решения прямой.

Составим, например, двойственную задачу к прямой задаче, которая решена выше симплексным методом.

Определить , который удовлетворяет условиям -ограничениям :

и обеспечивает минимальное значение целевой функции

Z( )=1100y1+120y2+8000y3 min

Таким образом, оптимальный план двойственной задачи имеет вид:

_

= (23,75; 12,5; 0; 0; 0; 5,75) =27625

По этим данным проводится анализ оптимального плана двойственной задачи по оценке ресурсов, используемых для реализации товаров.

 

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Как сформулировать экономическую постановку двойственной задачи к задаче планирования торгового процесса?

2. Как записывается математическая модель прямой и двойственной задач?

3. Каков план построения двойственной задачи?

4. Как определяется сопряженные пары переменных : прямой и двойственной задач?

 

4. ТРАНСПОРТНАЯ ЗАДАЧА ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ

Транспортная задача заключается в определении оптимального плана перевозок некоторого однородного груза из m пунктов от­правления в пунктов потребления .

Рассмотрим транспортную задачу, где в качестве критерия оптимальности является стоимость перевозок всего груза, которая должна быть минимальной.

 

Введем обозначения:

запасы груза в ом пункте отправления ;

величина заказа на этот груз в ом пункте назначения ;

стоимость перевозки единицы груза из А го пункта отправления в В ый пункт потребления (тариф перевозок);

- количество груза, доставленного из пункта в пункт, 0 •

Определить план перевозок груза из пунктов отправления в пункты назначения так, чтобы: вывести все грузы от поставщиков; удовлетворить заявки каждого потребителя; обеспечить минимальные транспортные расходы на перевозку груза.

Все исходные данные транспортной задачи можно записать в виде транспортной таблицы 4.

Таблица 4

Пункты отправления Пункты назначения Запасы
В1 … …  
… …
… …
… … … … … … … …
… …
… … … … … … … …
… …
Заявки … …

где - суммарный запас груза у поставщиков;

- суммарная величина заявок потребителей.

Математическая постановка транспортной задачи заключается в определении матрицы

', ,которая удовлетворяет следующим условиям:

а) Всякое неотрицательное решение системы линейных уравнений, определяемое матрицей

', называется допустимым планом транспортной задачи.

б) Ранг матрицы, составленный из коэффициентов при неизвестных системы линейных уравнений транспортной задачи, на единицу меньше числа уравнений, т.е. равен . Следовательно, число линейно независимых уравнений равно , они образуют базис, а соответствующие им переменных будут являться базисными.

в) Допустимый план транспортной задачи, имеющий не более отличных от нуля величин , называется опорным.

 

г) Если в опорном плане число отличных от нуля компонент равно в точности , то план является невырожденным, если меньше, то план называется вырожденным.

д) План ', при котором функция 4 принимает свое минимальное значение, называется оптимальным планом транспортной задачи.

е) Для решения транспортной задачи необходимо и достаточно, чтобы суммарные запасы груза в пунктах отправления были равны сумме заявок пунктов назначения:

ж) Модель транспортной задачи, удовлетворяющая этому условию, называется закрытой. Если же указанное условие не выполняется, то модель называется открытой.

В случае превышения запаса над заявками:

вводится фиктивный пункт назначения с потребностью

= и соответствующие тарифы считаются равными нулю: .

При вводится фиктивный (m+1) пункт отправления с запасом груза = , итарифы принимаются равными нулю:

Рассмотрим один из методов построение первого опорного плана - метод наименьших тарифов.

з) Наилучшим элементом матрицы тарифов называется наименьший тариф, если задача поставлена на минимум, наибольший тариф - если задача поставлена на максимум целевой функции.

Алгоритм построения первого опорного плана методом наименьшей стоимости включает следующие этапы.

1. Среди тарифов находится наименьший.

2. Клетку с выбранным тарифом заполняем максимально возможным объемом груза с учетом ограничений по строке и столбцу, при этом либо весь груз вывозится от соответствующего поставщика, либо полностью удовлетворяется заявка потребителя. Строка или столбец таблицы вычеркивается и в дальнейшем распределении не участвует.

3. Из оставшихся тарифов вновь находим наилучший, и процесс продолжается до тех пор, пока не будет распределен весь груз.

Если модель транспортной задачи открытая и введены фиктивный поставщик или потребитель, то распределение осуществляется сначала для действительных поставщиков и потребителей, и в последнюю очередь нераспределенный груз направляется от фиктивного поставщика или к фиктивному потребителю.

Дальнейшее улучшение первого опорного плана и получение оптимального плана производим методом потенциалов.

и) План транспортной задачи будет являться оптимальным, если существует система m+n чисел называемых потенциалами, удовлетворяющая условиям:

- для занятых клеток, где >0

для свободных клеток, где =0

при решении задачи на минимум, а при решении задачи на максимум:

для занятых клеток, где >0

для свободных клеток, где =0,

Потенциалы и являются переменными двойственной транспортной задачи и обозначают оценку единицы груза в пунктах отправления и назначения соответственно.

Введем обозначение оценки свободной клетки таблицы:

Если среди оценок нет отрицательная (задача поставлена на минимум), то опорный план является оптимальным и все сво­бодные клетки потенциальны.

Алгоритм метода потенциалов включает следующие этапы.

1. Построение первого опорного плана.

2. Проверка вырожденности плана.

Потенциалы и могут быть рассчитаны только для невырожденного плана. Если число занятых клеток в опорном плане меньше, чем , то вносим нуль в одну из свободных клеток таблицы так, чтобы общее число занятых клеток стало равным . Нуль вводят в клетку с наилучшим тарифом одного из одновременно вычеркиваемых рядов таблицы. При этом фиктивно занятая нулем клетка не должна об­разовывать замкнутого контура с другими клетками таблицы.

3. Определение значения функции цели путем суммирования произведений тарифов (удельных затрат) на объем перевозимого груза по всем занятым клеткам таблицы.

 

4. Проверка условия оптимальности.

Определением потенциалы и . Для каждой занятой

клетки таблицы записываем уравнение

( ; ). Получим систему уравнений с пе­ременными.

Так как число переменных больше числа уравнений , то система не определена и имеет бесчисленное множество решений. Одному из неизвестных , придают произвольное значение, например, для простоты вычислений полагаем =0. Тогда остальные потенциалы определяются из приведенных соотношений.

В транспортную таблицу добавляется дополнительная строка и столбец, куда заносятся потенциалы.

Определяем оценки свободных клеток .

Если все > О (задача решается на минимум целевой функции) либо все < 0 (задача решается на максимум целевой функции) , то оптимальный план найден. Если хотя бы одна оценка свободной клетки <0 (задача поставлена на минимум), >0 (задача поставлена на максимум), план не оптимальный, его можно улучшить , осуществив перераспределение груза.

5. Построение нового опорного плана.

Из всех положительных оценок свободных клеток выбираем наибольшую (если задача поставлена на минимум), из отрицательных - наибольшую по абсолютной величине (если задача поставлена на максимум). Клетку, которой соответствует наибольшая оценка, следует заполнить, т.е. направить груз. Заполняя выбранную клетку, необходимо изменить объемы поставок, записанных в ряде других занятых клеток и связанных с заполнением, так называемым циклом.

Циклом или прямоугольным контуром в таблице условий транспортной задачи называется ломаная линия, вершины которой расположены в занятых клетках таблицы, а звенья - вдоль строк и столбцов, причем в каждой вершине цикла встречаются ровно два звена, одно из которых находится в строке, другое - в столбце. Если ломаная линия, образующая цикл, пересекается, то точки пересе­чения не являются вершинами. Для каждой свободной клетки таблицы можно построить единственный цикл.

Вершинам цикла, начиная от вершины, находящейся в свободной клетке, присваиваем поочередно знаки "+" и "-".

Из объемов груза, стоящих в минусовых клетках, выбираем наименьшее и обозначим его 9. Перераспределяем величину 8 по циклу, прибавляя ее к соответствующим объемам грузов, стоящим в минусовых клетках. Клетка, которая ранее была свободной, становится занятой, а одна из занятых клеток цикла становится свобод­ной. В результате получаем новый опорный план и возвращаемся к четвертому этапу алгоритма.

 

ЗАМЕЧАНИЯ

1. Если в минусовых клетках построенного цикла находятся два (или несколько) одинаковых минимальных значения , то при перераспределении объемов груза освобождаются две (или несколько) клеток, и план становится вырожденным. Для продолжения решения необходимо в одну (или несколько) одновременно освобождающихся клеток направить нуль, причем предпочтение отдается клетке с наилучшим тарифом. Нулей вводится столько, чтобы во вновь полученном опорном плане число занятых клеток было равно (m+n-1).

2. Если в оптимальном плане транспортной задачи оценка для некоторой свободной клетки =0 , то задача имеет множество оптимальных планов. Для клетки с нулевой оценкой можно построить цикл и перераспределить груз. В результате полученный план будет также оптимальным.

3. Значение функции цели на каждой интеракции можно рассчитать следующим образом:

· задача поставлена на min,

· задача поставлена на max, где при переходе к новому плану;

- значение функции цели на k-итерации;

- значение функции цели на предыдущей (k-1)- итерации.

Пример решения транспортной задачи

На три базы поступил однородный груз в количествах, соответственно равных 6, 8, 10 (ед.) Этот груз требуется перевезти в четыре магазина соответственно в количествах 4, 6, 8, 8 (ед.). Стоимость доставки единицы груза с каждого из пункта отправления в соответствующие

пункты назначения заданы матрицей тарифов (в руб.):