Сочетания

 

В тех случаях, когда не имеет значения порядок элементов в подмножестве некоторого множества, а лишь его состав, говорят о сочетаниях. К сочетаниям без повторений приводит следующая задача комбинаторики.

Сколько -элементных подмножеств с различными элементами можно составить из элементов -множества ?

Такие подмножества называют сочетаниями без повторений из элементов по или короче 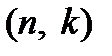-сочетаниями, а их число обозначают (от французского слова combinaison – сочетание). Другими словами, сочетаниями без повторений называется неупорядоченная 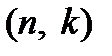-выборка, в которой элементы не повторяются.

Формулу для числа сочетаний легко получить из формулы (2) для числа размещений. Выберем какое-нибудь -элементное подмножество . Его можно упорядочить способами, а число таких подмножеств есть . Тогда справедлива формула

, (5)

откуда

. (6)

Пример 5. Сколько всего партий играется в шахматном турнире с участниками?

Ответ: , так как каждая партия однозначно определяется двумя ее участниками.

Пусть множество состоит из элементов различных типов: . Множество , составленное из , в котором элементы могут повторяться, называется мультимножеством. Для задания мультимножества надо указать число вхождений в него каждого элемента:

,

где – мощность мультимножества.

Число мультимножеств мощности , составленных из элементов -множества , называют сочетаниями с повторениями и обозначают . Другими словами, сочетаниями с повторениями называется неупорядоченная 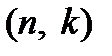-выборка, в которой элементы могут повторяться.

. (7)

Пример 6. В кондитерском магазине продавались 4 сорта пирожных: наполеоны, эклеры, песочные и слоеные. Сколькими способами можно купить 7 пирожных?

Решение. Мощность мультимножества , число различных элементов . Число способов покупки пирожных равно .