Вывод: все животные в этом дворе грызут кости.

Представим все высказывания в дизъюнктивной форме.





|



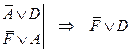
|



|


|
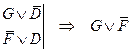
|
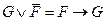 - что и требовалось доказать - что и требовалось доказать
|
Задача 2.Сформулировать представленную выше задачу на языке логики предикатов и упростить полученную систему используя теоремы и тождества логики предикатов.

Тождество доказано.
Задача 3.Сконструировать машину Тьюринга (написать соответствующую программу) для решения следующей задачи.
На ленте машины Тьюринга содержится последовательность символов “+”. Напишите программу для машины Тьюринга, которая каждый второй символ “+” заменит на “–”. Замена начинается с правого конца последовательности. Автомат в состоянии q1 обозревает один из символов указанной последовательности. Кроме самой программы-таблицы, описать словами, что выполняется машиной в каждом состоянии.

В состоянии q1 машина ищет правый конец числа, в состоянии q2 — пропускает знак “+”, при достижении конца последовательности — останавливается. В состоянии q3машина знак “+” заменяет на знак “–”, при достижении конца последовательности она останавливается.
Задача 4.Записать логическую функцию, соответствующую высказыванию:
А – «Допоздна работаешь с компьютером», В – «Пьешь много кофе», С – «Утром встаешь в дурном расположении духа», D – «Утром встаешь с головной болью». Составное высказывание «Если допоздна работаешь с компьютером и при этом пьешь много кофе, то утром просыпаешься в дурном расположении духа или с головной болью».
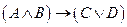
Задача 5.Записать сложное высказывание «Если компьютер при запуске выдает ошибку при проверке оперативной памяти (A) и память установлена правильно (B), то оперативная память дефектна (C) и дефектна материнская плата (D)» логической формулой и минимизировать его, используя карту Карно.
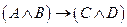

| 
| 
| 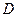
| 
| 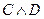
| 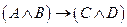
|

В нашем случае:  ,
, 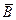 ,
, 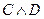 .
.
Значит  .
.
Задача 6.Каждой пропозициональной форме, содержащей n различных пропозициональных букв, соответствует таблица истинности с 2n строками.
Составить таблицу истинности для следующей формы:


| 
| 
| 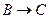
| 
| 
| 
| 
| 
|
Задача 7.Составить рекуррентное выражение для вычисления функции (n +1)! + 2, представив функции h(n, m) и g(n).





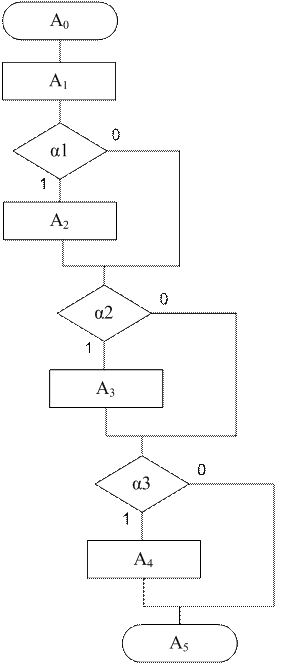
Задача 8. Представить на языке ГСА (операторные вершины обозначить буквами А1, А2, …, Аn, а логические – буквами α1, α2, …, αm), используя рекомендуемые ГОСТом обозначения, алгоритм решения следующей задачи.
Найти максимальное из четырех представленных чисел A, B, C и D, не используя понятие массива.
Введем обозначения:
A0 – «начало»
А1 – «x = A»
А2 – «x = В»
А3 – «x = С»
А4 – «x = D»
А5 – «конец»
α1 – «x < В»
α2 – « x < С»
α3 – « x < D»
Задача 9. Представленный в предыдущем задании алгоритм перевести с языка ГСА на язык ЛСА (используя обозначения предыдущей задачи).
А0А1 α1↑1А2↓1α2↑2А3↓2α3↑3А4↓3А7
Библиографический список
1. Игошин В.И. Задачи и модели по математической логике и теории алгоритмов. – 2-е изд. – М.: Академия, 2006. – 304 с.
2. Тимофеева, И.Л. Математическая логика: курс лекций: учеб. пособие. – 2-е изд. – М.: КДУ, 2007.
3. Гладкий А.В. Математическая логика и теория алгоритмов. – М.: МЦНМО, 2001.
4. Зюзьков В.М, Шелупанов А.А. Математическая логика и теория алгоритмов: Учебное пособие для вузов. – 2-е изд. – М.: Горячая линия–Телеком, 2007. – 176 с.
5. Игошин В.И. Задачник-практикум по математической логике: уч. пособие. – М.: Академия, 2006.
6. Галиев Ш.И. Математическая логика и теория алгоритмов. – Казань: Издательство КГТУ им. А.Н. Туполева. 2002. – 270 с.