Общие теоретические сведения
Одним из фундаментальных в статистическом анализе является понятие случайной величины. Случайной называется переменная величина, принимающая те или иные значения с определенными вероятностями.
В практических задачах обычно используются дискретные и непрерывные случайные величины. Дискретной случайной величиной называется такая случайная величина, множество возможных значений которой либо конечно, либо бесконечно, но счетно. Непрерывной случайной величиной называется такая случайная величина, которая может принять любое значение из некоторого конечного или бесконечного интервала. Чтобы дать полное математическое описание случайной величины, нужно указать множество ее значений и соответствующее случайной величине распределение вероятностей на этом множестве.
Каждое отдельное значение непрерывной случайной величины обладает нулевой вероятностью. Однако, несмотря на данное обстоятельство, нахождение возможных значений случайной величины в различных интервалах обладает различными отличными от нуля вероятностями. Для этого используют понятие функции распределения случайной величины.
Функцией распределения случайной величины X называется функция F(x), задающая вероятность того, что случайная величина X принимает значение, меньшее х, т.е.
F(x)=P(X<x) (8.1)
Иногда функцию F(x) называют интегральной функцией распределения. Для дискретной случайной величины интегральная функция распределения будет выглядеть следующим образом:
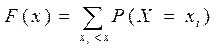 (8.2)
(8.2)
Функция распределения вероятностей непрерывной случайной величины дает полную вероятностную характеристику ее поведения. Однако способ задания непрерывной случайной величины с помощью функции распределения не является единственным. Ее можно задать с помощью другой функции, которая называется дифференциальной функцией распределения или плотностью распределения. В некотором смысле эта функция более удобна, чем интегральная функция F(x), так как последняя не в полной мере дает представление о характере распределения случайной величины в небольшой окрестности той или иной точки числовой оси.
Решить эту задачу позволяет дифференциальная функция распределения, которая является первой производной интегральной функции распределения:
f(х)=F’(х) (8.3)
График дифференциальной функции распределения f(x) называется кривой распределения. Кривая распределения, выражающая общую закономерность данного типа распределения, называется теоретической кривой распределения.
В статистике широко используются различные виды теоретических распределений — нормальное распределение, биномиальное, распределение Пуассона и др. Каждое из теоретических распределений имеет специфику и свою область применения.