Проблема измерения в квантовой механике.

Не менее важным является вопрос, касающийся квантовых пределов точности измерений. Одной из актуальнейших проблем в современной науке на сегодняшний день и в материаловедении в частности, является так называемая проблема «толстых пальцев», под которой подразумевается сложность манипулирования микро- и наночастицами. Н. Бор сформулировал один из основополагающих принципов квантовой механики – так называемый принцип дополнительности, согласно которому невозможно точно измерить одну физическую величину микрообъекта без потери информации о величине, дополнительной к ней. В 1927 г. В. Гейзенберг установил так называемый принцип неопределённости, согласно которому: невозможно одновременно точно осуществить одновременное измерение координаты и импульса микрочастицы. Это означает, в свою очередь, что осуществление измерения одной величины, исключает возможность измерения другой физической величины, дополнительной к ней. При этом, чем точней будет измерена координата микрочастицы, тем больше будет неопределённость в измерении её импульса, и наоборот. Постановка вопроса об одновременной измеримости динамических величин является типично квантово-механической. В классической динамике каждая физическая величина строго детерминирована – в одинаковых условиях всегда воспроизводится 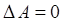. В квантовой механике равенство 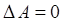возможно лишь при условии равенства , в котором вектор – одно из собственных состояний 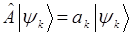. Если же для заданного значения флуктуирующих величин 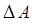и равны нулю, то есть есл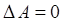и и 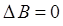, то естественно говорить об одновременной измеримости динамических переменных и в состоянии . Но это означает, что является одновременно собственным вектором и для , и для 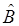. Данная задача нами уже рассматривалась при обсуждении теории представлений в квантовой механики. Вернёмся теперь и рассмотрим последнюю более подробней. В основе подобного рассмотрения лежат введенные нами уже ранее так называемые коммутационные соотношения. Основываясь на свойствах коммутаторов, решают задачу об одновременной измеримости двух динамических переменных (физических величин) в квантовой механике. Действительно, пусть у нас имеется две взаимосвязанные динамические переменные (физические величины), которым отвечают соответствующие им квантово-механические операторы и . При этом каждому из операторов соответствует свой набор собственных значений физической величины, которой в квантовой механике ставится в соответствие линейный самосопряжённый оператор. В квантовой механике взаимосвязь между операторами и динамическими переменными (физическими величинами) – оригиналами и их отображениями, выражается соответствующими операторными уравнениями вида:

тогда соответственно:

Для решения принципиального вопроса касающегося одновременной измеримости двух взаимосвязанных физических величин (динамических переменных), составим соответствующее этим операторам коммутационное соотношение. При этом если данные операторы будут коммутировать между собой, т.е. если , то имеется отличная от нуля возможность одновременного измерения соответствующих этим операторам динамических переменных. Отличие же коммутаторов от нуля, т.е. если , указывает на то, что совместное измерение двух динамических переменных (физических величин) в квантовой механике невозможно (операторы не коммутируют между собой), имеем соответственно:

и таким образом:

Это в свою очередь находится в полном соответствии с принципом неопределённости В. Гейзенберга, отрицающего возможность одновременного измерения двух динамических переменных (физических величин). Тогда система уравнений в общем виде:

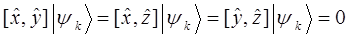
будет представлять собой математическое выражение принципа неопределённости В. Гейзенберга, сформулированного на языке операторов квантовой механики. Итак, условием одновременной измеримости двух динамических величин (переменных) является обращение в нуль их коммутатора:

Если же коммутатор не обращается в нуль, т.е. при условии, что:

то на основании выражения:

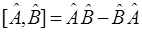
можно оценить меру одновременной неизмеримости и . При этом в общем случае можно показать, что для произведения двух флуктуаци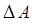й и оказывается справедливым неравенство Гейзенберга:

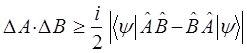
учитывая, что:

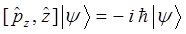
или

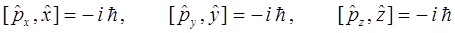
в чём убеждаемся на основании соответствующих выкладок:

и аналогично:

а также, что:

имеем соответственно:

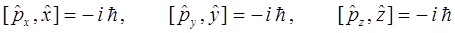
или

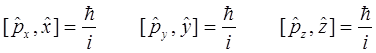
Подставляя полученные значения для коммутаторов в неравенство Гейзенберга:

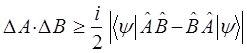
будем иметь соответственно:

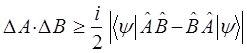
и таким образом:

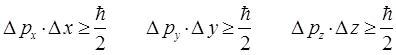
Отсюда следует, что если точно определить координату частицы, то ничего нельзя сказать об её импульсе и наоборот. Из соотношения неопределённости следует, что чем точнее определено значение одной из входящих в него величин, тем менее определено будет значение другой, дополнительной к ней величины. Другая пара величин, связанных между собой соотношением неопределённостей – это энергия системы и время , в течение которого система имеет это значение энергии:

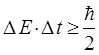
Отсюда следует, что если имеется возможность наблюдать динамическую систему в течение времени 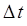, то её энергия может быть определена с точностью:

Таким образом, соотношение неопределённостей устанавливает фундаментальные, принципиально непреодолимые пределы точности измерений. Можно даже сказать, что природа позволяет изучать себя с точностью только до соотношения неопределённостей и не более того. Не один эксперимент не может привести к одновременному и точному измерению величин, которые являются дополнительными друг к другу. Принцип неопределённости часто объясняют влиянием измерительного прибора на частицы. С одной стороны, это оправдано, поскольку большинство измерительных приборов, так или иначе, являются макроскопическими, грубыми по отношению к размерам квантовых объектов. Понятно, что чем больше техническое несовершенство измерительного прибора, тем менее определёнными (точными) будут измерения. С другой стороны, неопределённость в измерениях связана не только с несовершенством измерительной техники, но и с объективными свойствами материи, так как любое измерение, как физический процесс, обязательно сопровождается каким-либо воздействием на объект в процессе измерения.