Уравнение Шрёдингера.
Правильный способ вычисления волновых функций микрочастиц был предложен в 1926 г. Э. Шрёдингером. Он также руководствовался оптико-механической аналогией Гамильтона и идеей де Бройля о корпускулярно-волновой природе микрочастиц, но исходным считал волновое уравнение:
В основе механики Шрёдингера лежат представления об аналогии между механическими колебаниями и волнами. Используя волновое уравнение классической теории электромагнитного излучения и соотношение де Бройля, связывающее импульс частицы с длиной волны 
, Э. Шрёдингер предложил свой вариант квантовой механики – волновую механику, получив уравнение, описывающее движение микрообъектов в пространстве. В 1927 г. В. Гейзенберг установил так называемый принцип неопределённости, согласно которому невозможно одновременно точно осуществить одновременное измерение координаты и импульса микрочастицы. Это означает, в свою очередь, что осуществление измерения одной величины, исключает возможность измерения другой физической величины. При этом, чем точней будет измерена координата микрочастицы, тем больше будет неопределённость в измерении импульса, и наоборот. В этом же самом году им была предложена так называемая матричная механика, основная идея которой состояла в том, что каждой наблюдаемой физической величине соответствовала определённая матрица. Э. Шрёдингером было показано, что матричная механика Гейзенберга, в конечном счете, сводится к волновой механике. Результатом этого стало объединение обеих подходов и возникновение квантовой механики. Квантовая механика занимает своеобразное положение в ряду физических теорий. Обычно более общая теория может быть сформулирована логически замкнутым образом не зависимо от менее общей теории, являющейся её предельным случаем. Так, релятивистская механика может быть построена на основании своих принципов, без всяких ссылок на ньютоновскую механику. Формулировка же основных положений квантовой механики, принципиально невозможна без привлечения механики классической. Таким образом, квантовая механика содержит в себе классическую в качестве своего предельного случая. Мало того, она нуждается в этом самом предельном случае для самого своего обоснования. При этом переход от классической механики к квантовой, осуществляется через механику колебаний и волн по-аналогии с тем, как происходит предельный переход от волновой к геометрической оптике. Необходимо подчеркнуть, что указанный выше предельный переход не только неизбежен, но и необходим. Он позволяет представить квантовую механику не как систему постулатов «загадочного» происхождения, а как стройную физическую теорию с определённым логическим выводом, терминологически и идейно следующим из классического подхода. Так, одной из основных задач классической механики является нахождение траектории движения частицы (или системы частиц). Для этого необходимо составить и решить уравнение движения и получить зависимость координат от времени. Зная координаты частицы в настоящий момент времени, можно предсказать её положение в любой последующий момент времени. В отличие от классической, квантовая механика включает в себя совершенно новую концепцию движения. В соответствии с принципом неопределённости Гейзенберга, для квантово-механической системы нельзя рассчитать траекторию движения. Следовательно, для описания движения не по траекториям квантовая механика должна использовать новые понятия и представления. Центральным понятием квантовой механики является волновая функция 
, которая по аналогии с гармоническими колебаниями и волнами характеризует распределение стоячих волн в пространстве. Данное понятие было введено в квантовую механику Шрёдингером. Волновая функция зависит от координат 
частиц и в общем случае от времени 
, тогда общее решение дифференциального уравнения для гармонического осциллятора в показательной форме:
может быть переписано в виде:
где выражения:
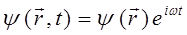
представляют собой частные решения соответствующего дифференциального уравнения. Необходимо отметить, что одно из частных решений будет комплексно сопряжённым другому. При этом суперпозиция соответствующих частных решений, образуют стоячую волну, состоящую из двух бегущих волн. Поскольку волновая функция 
- комплексная величина, т.е.
то физический смысл будет иметь не сама волновая функция 
, а квадрат её модуля 
. По аналогии со световыми волнами, квадрат амплитуды пропорционален интенсивности волны. Интенсивность волны, с точки зрения квантовой теории света, равнозначна числу световых квантов (фотонов) в единице объёма, а для единичного фотона – вероятности его нахождения в единице объёма. Проводя аналогию между светом и веществом далее, можно считать, что интенсивность волны де Бройля или определяет число частиц в единице объёма. Если рассматривать единичную частицу, то квадрат амплитуды 
даёт вероятность нахождения частицы в единице объёма или плотность вероятности:
Очевидно, произведение плотности вероятности на элементарный объём 
- есть вероятность нахождения частицы в элементарном объёме, т.е. в области с координатами 
и 
, 
и 
, 
и 
. Таким образом, амплитуда волны де Бройля получает статистическое истолкование, а для единичной частицы – вероятностное толкование. Квадрат амплитуды волны де Бройля равен вероятности нахождения частицы в единице объёма, её плотности вероятности. Аналитически данное положение, являющееся одним из постулатов квантовой механики, задаётся выражением вида:
Этот постулат был выдвинут впервые в 1928 г. М. Борном. Волны де Бройля – это волны вероятности, они не материальны, т.е. не связаны с каким-либо переносом энергии. Отсюда становится понятным, почему при рассмотрении волнового процесса, в качестве модели выбирают так называемые стоячие волны, распространение которых не связано с переносом энергии и потому являющиеся стабильными, постоянными во времени. Итак, в квантовой механике описание состояния частицы (или системы частиц) выполняется с помощью волновой функции , которая описывает распределение вероятностей нахождения этой частицы (или системы частиц) в пространстве. Статистическая интерпретация как вероятности нахождения частицы в элементе объёма , находится в полном соответствии с принципом неопределённости Гейзенберга. В оптике волновая функция находится как решение дифференциального уравнения волны. Аналогично в квантовой механике существует дифференциальное уравнение для волн де Бройля, из которого находят волновую функцию описывающую распределение электронной плотности в микросистемах. Для вывода такого уравнения на основании оптико-механической аналогии Гамильтона, найдём изначально стационарные решения волнового уравнения, строго зависящие от частоты 
, имеем соответственно:
При этом получаемые решения должны удовлетворять требованиям регулярности и граничному условию. К требованиям регулярности относят: конечность, однозначность, и непрерывность волновой функции. Требование конечности означает, что величины и не могут принимать бесконечно большие значения. Однозначность волновой функции означает, что вероятность найти частицу в данном элементарном объёме - всегда строго определённая, большая или малая, но всегда одна. Непрерывность волновой функции означает, что нет такого элементарного объёма 
, где нельзя было бы определить вероятность нахождения микрочастицы. Граничное условие – обращение волновой функции в нуль на бесконечности. Данное условие означает, что частицу всегда можно найти в каком-то строго локализованном участке пространства. Кроме того, волновая функция должна подчиняться условиям нормировки и ортогональности. Ортогональные и нормированные волновые функции называют также ещё ортонормированными. Условие одновременной ортогональности и нормированности волновой функции можно записать, используя символ Кронекера 
. Таким образом, имеем соответственно:
Основываясь на хорошо известной из математики теореме о полной вероятности, можно утверждать, что вероятность обнаружить частицу во всём объёме равна сумме вероятностей во всех точках этого пространства и равна единице. Действительно, если электрон находится в некотором объёме 
и известна волновая функция электрона 
. Тогда при разбиении объёма на бесконечно малое число элементарных объёмов 
, 
, 
, …, 
, вероятность обнаружить электрон в каждом из элементарных объёмов будет очевидно определяться выражениями вида:
.……………………….
Поскольку вероятность достоверного события равна единице, то очевидно полная вероятность (вероятность нахождения электрона во всём объёме ) равна сумме вероятностей отдельных событий и равна единице:
Переходя к бесконечно малым элементам объёма, суммирование можно заменить интегралом вида:
Из условия нормировки также следует, что волны вероятности 
и 
соответствуют одинаковым состояниям микрочастицы. Нормированность волновой функции показывает, что вероятность нахождения микрочастицы в элементарном объёме всегда конечна и равна единице. Ортогональность волновых функций определяется выражением вида:
откуда следует, что волны вероятности и соответствуют различным состояниям микрочастицы. Ортогональность волновых функций определяет их линейную независимость, т.е. не одна из них не содержит в себе примеси другой, в чём хорошо проявляется принцип суперпозиции состояний системы. Поскольку по определению волновая функция должна быть конечной, т.е. величины и не могут принимать бесконечно большие значения, тогда в соответствии с принципом конечности, стационарное (не зависящее от времени), решение выбираем в виде:
Рассматривая для простоты выкладок одномерный случай, будем иметь соответственно:
Легко показать, что выбранное в соответствии с описанными выше физически осмысленными условиями решение, соответствует уравнению плоской волны де Бройля, имеющей вид:
учитывая, что величине смещения 
, амплитуды волны в квантовой механике соответствует волновая функция 
, тогда соответственно будем иметь:
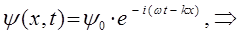
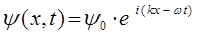
из полученного уравнения достаточно хорошо видно, что волновая функция есть произведение координатной волновой функции на член, выражающий зависимость её от времени, т.е.
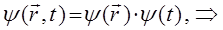
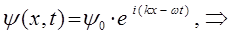
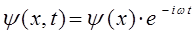
Найдём сначала стационарные решения волнового уравнения:
то есть решения, строго периодически зависящие от частоты ω. Для этого продифференцируем выражение для плоской волны де Бройля, записанное через волновую функцию по времени t:
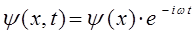
используя соотношения:
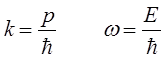
несложно показать, что уравнение для плоской волны де Бройля:
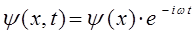
принадлежит именно такому классу решений:
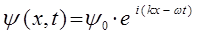
или что то же самое:
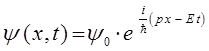
Таким образом, имеем соответственно:
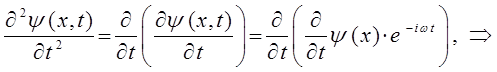
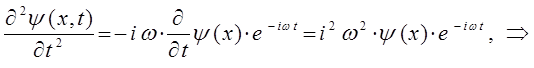
или для общего случая:
подстановка полученного равенства в уравнение:
приводит последнее к виду, уже не содержащему время:
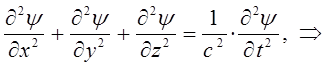
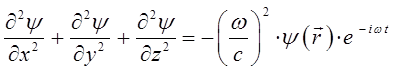
учитывая, что:
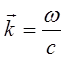
и соответственно:
имеем соответственно:
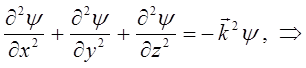
Полученное уравнение нами выше уравнение является всё ещё результатом классической волновой теории. Оно было известно ранее как уравнение Гельмгольца. Переходя от механических величин к квантовым, путём отождествления волнового вектора 
с волновым числом, на основании уравнения:
будем иметь соответственно:
и таким образом:
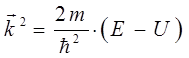
Подставляя полученное выражение для волнового вектора в уравнение:
имеем соответственно:
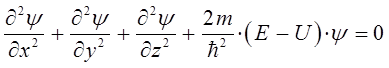
или после соответствующих преобразований:
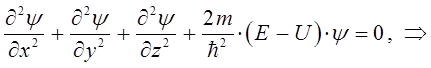
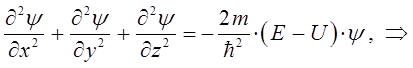
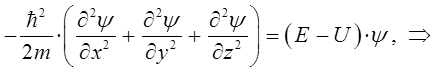
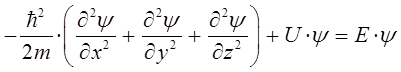
Полученное в ходе проделанных выкладок уравнение, называется стационарным уравнением Шрёдингера для одной частицы с произвольным потенциалом 
. Данное уравнение можно также получить и другим способом. Для этих целей необходимо продифференцировать выражение для плоской волны де Бройля сначала по координате, а затем по времени, учтя независимость данных операций и далее подставить результаты дифференцирования в соответствующее волновое уравнение. Таким образом, будем иметь соответственно:
аналогично дифференцирование выражение для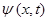 
по , имеем:
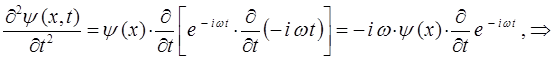
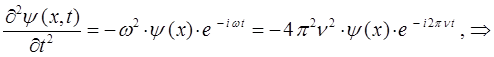
Таким образом, в ходе проделанных операций дифференцирования, мы пришли к выражениям вида:
исходя из вида волнового уравнения, полученного уже ранее:
имеем соответственно:
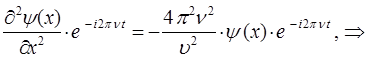
по аналогии с электромагнитными волнами, для которых справедливы соотношения:
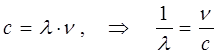
и условие:
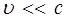
данные соотношения можно переписать в виде:
тогда соответственно:
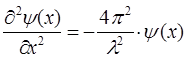
нетрудно заметить, что:
и таким образом, выражение вида:
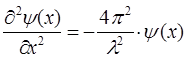
становится эквивалентным тому, что решалось нами в задаче на гармонический осциллятор, где вместо величины смещения 
используется в силу специфики микрообъектов – волновая функция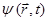 
. Тогда соответственно, записывая полученное выше уравнение через волновой вектор 
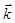, будем иметь соответственно:
учитывая уравнение, связывающее волновой вектор с импульсом микрочастицы:
и выражение, описывающее её кинетическую энергию:
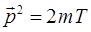
будем иметь соответственно:
откуда соответственно:
поскольку:
тогда, следовательно:
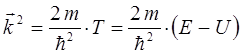
подстановка значения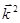 
в соответствующее волновое уравнение, даёт выражение вида:
Распространяя данное уравнение на случай трёх пространственных декартовых координат, будем иметь соответственно:
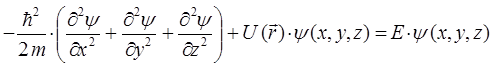
Опуская индексы, делающие полученное уравнение более громоздким, можно записать, что:
или в более компактном виде:
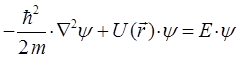
здесь:
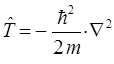
Преобразуя полученное выражение, приходим к уравнению:
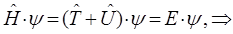
Полученное выражение представляет собой стационарное уравнение Шрёдингера в операторной форме. Это есть частный случай более общей задачи на собственные значения оператора:
имеющей в квантовой механике принципиальное значение. Полученное стационарное уравнение Шрёдингера может быть далее обобщено на случай нестационарных (протекающих во времени) процессов. Для получения нестационарного уравнения Шрёдингера, необходимо преобразовать выражение:
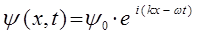
к виду, используя соответствие между импульсом и волновым вектором, энергией и циклической (круговой) частотой, т.е.
тогда соответствующее выражение для плоской волны де Бройля, с учётом этих условий, после подстановки значений 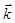и , перепишется в виде:
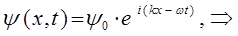
Поскольку гамильтониан есть дифференциальный оператор, то очевидно для нестационарных процессов, его действие при решении задачи на собственные значения оператора будет сводиться к нахождению частной производной по времени от функции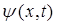 
; так, имеем соответственно:
при этом учитывая, что значение амплитуды волны де Бройля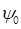 
будет находиться и в правой, и в левой частях тождества и как следствие сократится, тогда соответственно:
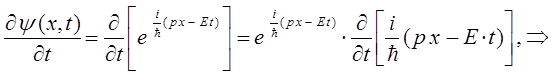
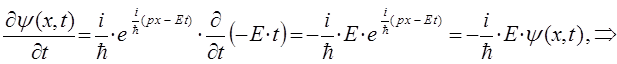
поскольку:
тогда:
учитывая, что:
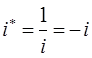
будем иметь соответственно:
постоянство энергии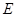 
позволяет сделать замену вида:
тогда соответственно:
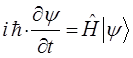
Таким образом, в ходе проделанных выкладок приходим к двум эквивалентным друг другу уравнениям:
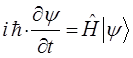
Полученные уравнения справедливы для произвольного гамильтониана, допускающего явную зависимость от времени. Уравнение Шрёдингера как линейное дифференциальное уравнение второго порядка в частных производных, имеет бесчисленное множество решений. Из них интерес представляют лишь такие, которые удовлетворяют требованиям регулярности и граничному условию. В обычных задачах квантовой химии при интерпретации свойств и структуры молекул, как правило, важны стационарные (не зависящие от времени) состояния. В стационарных состояниях плотность вероятности, электронная плотность, а также и другие физические величины не зависят от времени. Можно показать, что нестационарное уравнение Шрёдингера:
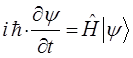
сводится к стационарному (не зависящему от времени) уравнению Шрёдингера. Для этого запишем волновую функцию для электрона, находящегося в стационарном состоянии:
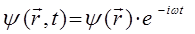
учитывая условия вида:
будем иметь соответственно:
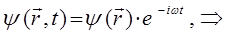
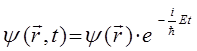
подставляя данное выражение в нестационарное уравнение Шрёдингера:
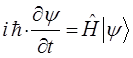
будем иметь соответственно:
продифференцируем левую часть данного операторного уравнения:
откуда будем иметь соответственно:
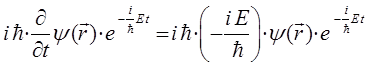
поскоipt async src="adsbygoogle.js">