Описание состояния микрообъектов в квантовой механике. Квантовые пределы точности измерений.

В 1926 г. руководствуясь оптико-механической аналогией Гамильтона и идеей де Бройля о корпускулярно-волновой природе микрочастиц, Э. Шрёдингер предложил свой вариант квантовой механики – волновую механику. В основе механики Шрёдингера лежат представления об аналогии между механическими колебаниями и волнами. Используя волновое уравнение классической теории электромагнитного излучения и соотношение де Бройля, связывающее импульс частицы с длиной волны , Э. Шрёдингер получил уравнение, описывающее движение микрообъектов в пространстве:

В 1927 г. В. Гейзенберг установил так называемый принцип неопределённости, согласно которому: невозможно одновременно точно осуществить одновременное измерение координаты и импульса микрочастицы. Это означает, в свою очередь, что осуществление измерения одной величины, исключает возможность измерения другой физической величины. При этом, чем точней будет измерена координата микрочастицы, тем больше будет неопределённость в измерении импульса, и наоборот. Так, на основании формулы де Бройля, имеем:

поэтому:

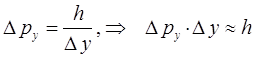
В этом же самом году им была предложена так называемая матричная механика, основная идея которой состояла в том, что каждой наблюдаемой физической величине соответствовала определённая матрица. Э. Шрёдингером было показано, что матричная механика Гейзенберга, в конечном счёте, сводится к волновой механике. Результатом этого стало объединение обеих подходов и возникновение квантовой механики. Одной из основных задач классической механики является нахождение траектории движения частицы (или системы частиц). Для этого необходимо составить и решить уравнение движения и получить зависимость координат от времени. Зная координаты частицы в настоящий момент времени, можно предсказать её положение в любой последующий момент времени. В отличие от классической, квантовая механика включает в себя совершенно новую концепцию движения. В соответствии с принципом неопределённости Гейзенберга, для квантово-механической системы нельзя рассчитать траекторию движения. Следовательно, для описания движения не по траекториям квантовая механика должна использовать новые понятия и представления. Центральным понятием квантовой механики является волновая функция , которая по аналогии с гармоническими колебаниями и волнами характеризует амплитуду (распределение) стоячих волн в пространстве. Данное понятие было введено в квантовую механику Э. Шрёдингером. Волновая функция зависит от координат частиц, т.е. от радиус-векторов и в общем случае от времени и обозначается , тогда общее решение дифференциального уравнения для гармонического осциллятора в показательной форме:

может быть записано в виде:

где выражения:

частные решения соответствующего дифференциального уравнения. Необходимо отметить, что одно из частных решений будет комплексно сопряжённым другому. При этом суперпозиция соответствующих частных решений, образует стоячую волну, состоящую из двух бегущих волн. Поскольку волновая функция - комплексная величина, т.е.

то физический смысл, очевидно, будет иметь не собственно волновая функция , а квадрат её модуля . По аналогии со световыми волнами, квадрат амплитуды пропорционален интенсивности волны. Интенсивность волны, с точки зрения квантовой теории света, равнозначна числу световых квантов (фотонов) в единице объёма, а для единичного фотона – вероятности его нахождения в единице объёма. Проводя аналогию между светом и веществом далее, можно считать, что интенсивность волны де Бройля или определяет число частиц в единице объёма. Если рассматривать единичную частицу, то квадрат амплитуды даёт вероятность нахождения частицы в единице объёма или плотность вероятности:

Очевидно, произведение плотности вероятности на элементарный объём - есть вероятность нахождения частицы в элементарном объёме, т.е. в области с координатами и , и , и . Таким образом, амплитуда волны де Бройля получает статистическое истолкование, а для единичной частицы – вероятностное толкование. Квадрат амплитуды волны де Бройля равен вероятности нахождения частицы в единице объёма, её плотности вероятности. Аналитически данное положение, являющееся одним из постулатов квантовой механики, задаётся выражением вида:

Этот постулат был выдвинут впервые в 1928 г. М. Борном. Волны де Бройля – это волны вероятности, они не материальны, т.е. не связаны с каким-либо переносом энергии. Отсюда становится понятным, почему при рассмотрении волнового процесса, в качестве модели выбирают так называемые стоячие волны, распространение которых не связано с переносом энергии и потому являющиеся стабильными, постоянными во времени. Итак, в квантовой механике описание состояния частицы (или системы частиц) выполняется с помощью волновой функции , которая описывает распределение вероятностей нахождения этой частицы (или системы частиц) в пространстве. Статистическая интерпретация как вероятности нахождения частицы в элементе объёма , находится в полном соответствии с принципом неопределённости Гейзенберга. В оптике волновая функция находится как решение дифференциального уравнения волны. Аналогично в квантовой механике существует дифференциальное уравнение для волн де Бройля, из которого находят волновую функцию описывающую распределение электронной плотности в микросистемах. Для вывода такого уравнения на основании оптико-механической аналогии Гамильтона, находят изначально стационарные решения волнового уравнения, строго зависящие от частоты :

при этом получаемые решения должны удовлетворять требованиям регулярности и граничному условию. К требованиям регулярности относят: конечность, однозначность, и непрерывность волновой функции. Требование конечности означает, что величины и не могут принимать бесконечно большие значения. Однозначность волновой функции означает, что вероятность найти частицу в данном элементарном объёме - всегда строго определённая, большая или малая, но всегда одна. Непрерывность волновой функции означает, что нет такого элементарного объёма , где нельзя было бы определить вероятность нахождения микрочастицы. Граничное условие – обращение волновой функции в нуль на бесконечности. Данное условие означает, что частицу всегда можно найти в каком-то строго локализованном участке пространства. Кроме того, волновая функция должна подчиняться условиям нормировки и ортогональности. Ортогональные и нормированные волновые функции называют также ещё ортонормированными. Условие одновременной ортогональности и нормированности волновой функции можно записать, используя символ Кронекера :

Основываясь на хорошо известной из математики теореме о полной вероятности, можно утверждать, что вероятность обнаружить частицу во всём объёме равна сумме вероятностей во всех точках этого пространства и равна единице:

Таким образом, условие нормировки является следствием этой математической теоремы. Действительно, если электрон находится в некотором объёме и известна волновая функция электрона . Тогда при разбиении объёма на бесконечно малое число элементарных объёмов , , , …, , вероятность обнаружить электрон в каждом из элементарных объёмов будет очевидно определяться выражениями вида:

………………………..

Поскольку вероятность достоверного события равна единице, то очевидно полная вероятность (вероятность нахождения электрона во всём объёме ) равна сумме вероятностей отдельных событий и равна единице:

Переходя к бесконечно малым элементам объёма, суммирование можно заменить интегралом вида:

Из условия нормировки также следует, что волны вероятности и соответствуют одинаковым состояниям микрочастицы. Нормированность волновой функции показывает, что вероятность нахождения микрочастицы в элементарном объёме всегда конечна и равна единице. Ортогональность волновых функций определяется выражением вида:

откуда следует, что волны вероятности и соответствуют различным состояниям микрочастицы. Ортогональность волновых функций определяет их линейную независимость, т.е. не одна из них не содержит в себе примеси другой, в чём хорошо проявляется принцип суперпозиции состояний системы. Таким образом, состояние частицы (системы частиц) в любой момент времени полностью описывается волновой функцией, характеризующей распределение стоячих волн в пространстве. Одной из основных задач классической механики является нахождение траектории движения частицы (или системы частиц). Для этого необходимо составить и решить уравнение движения и получить зависимость координат от времени. Зная координаты частицы в настоящий момент времени, можно предсказать её положение в любой последующий момент времени. В отличие от классической, квантовая механика включает в себя совершенно новую концепцию движения. В соответствии с принципом неопределённости Гейзенберга, для квантово-механической системы нельзя рассчитать траекторию движения. Следовательно, для описания движения не по траекториям квантовая механика должна использовать новые понятия и представления. Центральным понятием квантовой механики является волновая функция , которая по аналогии с гармоническими колебаниями и волнами характеризует амплитуду (распределение) стоячих волн в пространстве. Данное понятие было введено в квантовую механику Э. Шрёдингером. Волновая функция зависит от координат частиц, т.е. от радиус-векторов и в общем случае от времени и обозначается , тогда общее решение дифференциального уравнения для гармонического осциллятора в показательной форме:

может быть записано в виде:

где выражения:

частные решения соответствующего дифференциального уравнения. Необходимо отметить, что одно из частных решений будет комплексно сопряжённым другому. При этом суперпозиция соответствующих частных решений, образуют стоячую волну, состоящую из двух бегущих волн. Сформулируем физические особенности стоячих волн:

ü Стоячая волна является по существу не волной, а колебательным процессом, происходящим в среде или теле. Поэтому определение волна (в строгом смысле этого слова) – к стоячим волнам не относится.

ü В реальной среде стоячая волна затухает в результате диссипации (рассеяния) энергии. Для поддержания стоячих волн, необходима их подпитка бегущей волной.

ü В стоячей волне все точки среды колеблются с разными амплитудами, а фазы колебаний точек по разную сторону от узла – противоположны, отличаясь на величину . В бегущей волне все точки среды колеблются с одинаковой амплитудой, одновременно в разных фазах.

ü В стоячей волне, в отличие от бегущей, нет переноса энергии. В ней происходит периодическое превращение одного вида энергии в другой – например, кинетической энергии в потенциальную и наоборот. Это обусловлено тем, что стоячая волна сформирована двумя бегущими волнами, распространяющимися и переносящими энергию в противоположных направлениях. Поскольку волновая функция - комплексная величина, т.е.

то физический смысл будет иметь не сама волновая функция , а квадрат её модуля . По аналогии со световыми волнами, квадрат амплитуды пропорционален интенсивности волны. Интенсивность волны, с точки зрения квантовой теории света, равнозначна числу световых квантов (фотонов) в единице объёма, а для единичного фотона – вероятности его нахождения в единице объёма. Проводя аналогию между светом и веществом далее, можно считать, что интенсивность волны де Бройля или определяет число частиц в единице объёма.

Если рассматривать единичную частицу, то квадрат амплитуды даёт вероятность нахождения частицы в единице объёма или плотность вероятности:

Этот постулат был выдвинут впервые М. Борном. Волны де Бройля – это волны вероятности, они не материальны, т.е. не связаны с каким-либо переносом энергии. Отсюда становится понятным, почему при рассмотрении волнового процесса, в качестве модели выбирают так называемые стоячие волны, распространение которых не связано с переносом энергии и потому являющиеся стабильными, постоянными во времени. Итак, в квантовой механике описание состояния частицы (или системы частиц) выполняется с помощью волновой функции , которая описывает распределение вероятностей нахождения этой частицы (или системы частиц) в пространстве. Статистическая интерпретация как вероятности нахождения частицы в элементе объёма , находится в полном соответствии с принципом неопределённости Гейзенберга. В оптике волновая функция находится как решение дифференциального уравнения волны. Аналогично в квантовой механике существует дифференциальное уравнение для волн де Бройля, из которого находят волновую функцию описывающую распределение электронной плотности в микросистемах. Для вывода такого уравнения на основании оптико-механической аналогии Гамильтона, найдём изначально стационарные решения волнового уравнения, строго зависящие от частоты , имеем соответственно:

При этом получаемые решения должны удовлетворять требованиям регулярности и граничному условию. К требованиям регулярности относят: конечность, однозначность, и непрерывность волновой функции. Требование конечности означает, что величины и не могут принимать бесконечно большие значения. Однозначность волновой функции означает, что вероятность найти частицу в данном элементарном объёме - всегда строго определённая, большая или малая, но всегда одна. Непрерывность волновой функции означает, что нет такого элементарного объёма , где нельзя было бы определить вероятность нахождения микрочастицы. Граничное условие – обращение волновой функции в нуль на бесконечности. Данное условие означает, что частицу всегда можно найти в каком-то строго локализованном участке пространства. Кроме того, волновая функция должна подчиняться условиям нормировки и ортогональности. Ортогональные и нормированные волновые функции называют также ещё ортонормированными. Условие одновременной ортогональности и нормированности волновой функции можно записать, используя символ Кронекера :

.……………………….

Переходя к бесконечно малым элементам объёма, суммирование можно заменить интегралом вида:

из условия нормировки также следует, что волны вероятности и соответствуют одинаковым состояниям микрочастицы. Нормированность волновой функции показывает, что вероятность нахождения микрочастицы в элементарном объёме всегда конечна и равна единице. Ортогональность волновых функций определяется выражением вида:

откуда следует, что волны вероятности и соответствуют различным состояниям микрочастицы. Ортогональность волновых функций определяет их линейную независимость, т.е. не одна из них не содержит в себе примеси другой, в чём хорошо проявляется принцип суперпозиции состояний системы. Не менее важным является вопрос, касающийся квантовых пределов точности измерений. Одной из актуальнейших проблем в современной науке на сегодняшний день является так называемая проблема «толстых пальцев», под которой подразумевается сложность манипулирования микро - и наночастицами. Н. Бор сформулировал один из основополагающих принципов квантовой механики – так называемый принцип дополнительности, согласно которому невозможно точно измерить одну физическую величину микрообъекта без потери информации о величине, дополнительной к ней. В 1927 г. В. Гейзенберг установил так называемый принцип неопределённости, согласно которому: невозможно одновременно точно осуществить одновременное измерение координаты и импульса микрочастицы. Это означает, в свою очередь, что осуществление измерения одной величины, исключает возможность измерения другой физической величины, дополнительной к ней. При этом, чем точней будет измерена координата микрочастицы, тем больше будет неопределённость в измерении импульса, и наоборот.

Отсюда следует, что если точно определить координату частицы, то ничего нельзя сказать об её импульсе и наоборот. Из соотношения неопределённости следует, что чем точнее определено значение одной из входящих в него величин, тем менее определено будет значение другой, дополнительной к ней величины. Другая пара величин, связанных между собой соотношением неопределённостей – это энергия системы и время , в течение которого система имеет это значение энергии:

Отсюда следует, что если имеется возможность наблюдать динамическую систему в течение времени , то её энергия может быть определена с точностью:

Таким образом, соотношение неопределённостей устанавливает фундаментальные, принципиально непреодолимые пределы точности измерений. Можно даже сказать, что природа позволяет изучать себя с точностью только до соотношения неопределённостей и не более того. Не один эксперимент не может привести к одновременному и точному измерению величин, которые являются дополнительными друг к другу. Принцип неопределённости часто объясняют влиянием измерительного прибора на частицы. С одной стороны, это оправдано, поскольку большинство измерительных приборов, так или иначе, являются макроскопическими, грубыми по отношению к размерам квантовых объектов. Понятно, что чем больше техническое несовершенство измерительного прибора, тем менее определёнными (точными) будут измерения. С другой стороны, неопределённость в измерениях связана не только с несовершенством измерительной техники, но и с объективными свойствами материи, так как любое измерение, как физический процесс, обязательно сопровождается каким-либо воздействием на объект в процессе измерения.