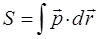Вариационные принципы механики.
Рассмотрим сначала частный случай динамики – статику: движение отсутствует, все обобщённые импульсы  и обобщённые силы
и обобщённые силы  равны нулю. Это в свою очередь равносильно экстремуму гамильтониана, а фактически потенциальной энергии U. В случае одной частицы статическое состояние системы задаётся условием исчезновения градиента U:
равны нулю. Это в свою очередь равносильно экстремуму гамильтониана, а фактически потенциальной энергии U. В случае одной частицы статическое состояние системы задаётся условием исчезновения градиента U:

В динамике, когда  , подобный по простоте принцип экстремума сформулировать нельзя. Однако при проведении некоторых параллелей между статикой и динамикой удаётся найти аналог стационарности, называемый также вариационным принципом. Как известно, потенциальное поле
, подобный по простоте принцип экстремума сформулировать нельзя. Однако при проведении некоторых параллелей между статикой и динамикой удаётся найти аналог стационарности, называемый также вариационным принципом. Как известно, потенциальное поле  изображают с помощью силовых линий. В этой связи напомним некоторые понятия теории поля. Так, к рассмотрению скалярных и векторных полей приводят многие задачи физики, механики, математики, электротехники и других технических наук. Изучение одних физических полей способствует изучению и других. Так, например, силы всемирного тяготения, магнитные, электрические силы – все они изменяются обратно пропорционально квадрату расстояния от своего источника; диффузия в растворах происходит по законам, общим с распространением тепла в различных средах; вид силовых магнитных линий напоминает картину обтекания препятствий жидкостью и т.д. Математическим ядром теории поля являются такие понятия, как градиент, поток, потенциал, дивергенция, ротор, циркуляция и другие. В общем случае полем называют область V пространства, в каждой точке которого определено значение некоторой величины. Если каждой точке M этой области соответствует определённое число
изображают с помощью силовых линий. В этой связи напомним некоторые понятия теории поля. Так, к рассмотрению скалярных и векторных полей приводят многие задачи физики, механики, математики, электротехники и других технических наук. Изучение одних физических полей способствует изучению и других. Так, например, силы всемирного тяготения, магнитные, электрические силы – все они изменяются обратно пропорционально квадрату расстояния от своего источника; диффузия в растворах происходит по законам, общим с распространением тепла в различных средах; вид силовых магнитных линий напоминает картину обтекания препятствий жидкостью и т.д. Математическим ядром теории поля являются такие понятия, как градиент, поток, потенциал, дивергенция, ротор, циркуляция и другие. В общем случае полем называют область V пространства, в каждой точке которого определено значение некоторой величины. Если каждой точке M этой области соответствует определённое число  , говорят, что в области определено (задано) скалярное поле (или функция точки). Иначе говоря, скалярное поле – это скалярная функция
, говорят, что в области определено (задано) скалярное поле (или функция точки). Иначе говоря, скалярное поле – это скалярная функция  вместе с её областью определения. Если же каждой точке M области пространства соответствует некоторый вектор
вместе с её областью определения. Если же каждой точке M области пространства соответствует некоторый вектор  , то говорят, что задано векторное поле (или векторная функция точки). Примерами скалярных полей могут быть поля температуры, атмосферного давления, плотности, электрического потенциала и т.д. Примерами векторных полей являются поле силы тяжести, поле скоростей частиц текущей жидкости (ветра), магнитное поле, поле плотности электрического тока и т.д. Если функция
, то говорят, что задано векторное поле (или векторная функция точки). Примерами скалярных полей могут быть поля температуры, атмосферного давления, плотности, электрического потенциала и т.д. Примерами векторных полей являются поле силы тяжести, поле скоростей частиц текущей жидкости (ветра), магнитное поле, поле плотности электрического тока и т.д. Если функция  или
или  не зависит от времени, то скалярное (векторное) поле называется стационарным. Поле, которое меняется с течением времени, называется нестационарным. Далее будем рассматривать только стационарные, не зависящие от времени поля. Если V – область трёхмерного пространства, то скалярное поле U можно рассматривать как функцию трёх переменных x, y, z (координат точки M):
не зависит от времени, то скалярное (векторное) поле называется стационарным. Поле, которое меняется с течением времени, называется нестационарным. Далее будем рассматривать только стационарные, не зависящие от времени поля. Если V – область трёхмерного пространства, то скалярное поле U можно рассматривать как функцию трёх переменных x, y, z (координат точки M):

Наряду с обозначениями  и
и  , используют запись
, используют запись  , где
, где  – радиус-вектор точки M. Если скалярная функция
– радиус-вектор точки M. Если скалярная функция  зависит только от двух переменных, например x и y, то соответствующее скалярное поле
зависит только от двух переменных, например x и y, то соответствующее скалярное поле  называют плоским. Аналогично, вектор
называют плоским. Аналогично, вектор  , определяющий векторное поле, можно рассматривать как векторную функцию трёх скалярных аргументов x, y и z –
, определяющий векторное поле, можно рассматривать как векторную функцию трёх скалярных аргументов x, y и z –  или
или  . Вектор
. Вектор  можно представить, разложив по ортам координатных осей, в виде:
можно представить, разложив по ортам координатных осей, в виде:

где  – проекции вектора
– проекции вектора  на оси координат. Если в выбранной системе координат
на оси координат. Если в выбранной системе координат  одна из проекций вектора
одна из проекций вектора  равна нулю, а две другие зависят только от двух переменных, то векторное поле называется плоским, например:
равна нулю, а две другие зависят только от двух переменных, то векторное поле называется плоским, например:

Векторное поле называется однородным, если  – постоянный вектор, в данном выражении P, R и Q – постоянные величины. Таким полем является поле силы тяжести. В дальнейшем будем предполагать, что скалярные функции
– постоянный вектор, в данном выражении P, R и Q – постоянные величины. Таким полем является поле силы тяжести. В дальнейшем будем предполагать, что скалярные функции  – определяющие скалярное поле и
– определяющие скалярное поле и  – задающие векторное поле, непрерывны вместе со своими частными производными. Рассмотрим скалярное поле, задаваемое функцией
– задающие векторное поле, непрерывны вместе со своими частными производными. Рассмотрим скалярное поле, задаваемое функцией  . Для наглядного представления скалярного поля используют поверхности линии уровня. Поверхностью уровня скалярного поля называется геометрическое место точек, в которых функция
. Для наглядного представления скалярного поля используют поверхности линии уровня. Поверхностью уровня скалярного поля называется геометрическое место точек, в которых функция  принимает постоянное значение, т.е.
принимает постоянное значение, т.е.

Придавая величине C различные значения, можно получить различные поверхности уровня, которые в совокупности как бы расслаивают поле. Через каждую точку поля проходит только одна поверхность уровня. Её уравнение очевидно можно найти путём подстановки координат точки в общее уравнение для поверхности уровня. Для случая плоского поля  равенство
равенство  представляет собой уравнение линии уровня поля, то есть линия уровня – это линия на плоскости
представляет собой уравнение линии уровня поля, то есть линия уровня – это линия на плоскости  , в точках которой функция
, в точках которой функция  сохраняет постоянное значение. Для характеристики скорости изменения поля
сохраняет постоянное значение. Для характеристики скорости изменения поля  в заданном направлении введём понятие производной по направлению.
в заданном направлении введём понятие производной по направлению.

Для этого возьмём в пространстве, где задано поле  , некоторую точку M и найдём скорость изменения функции U при движении точки M в произвольном направлении
, некоторую точку M и найдём скорость изменения функции U при движении точки M в произвольном направлении  . Пусть вектор
. Пусть вектор  имеет начало в точке M и направляющие косинусы
имеет начало в точке M и направляющие косинусы 

 . Приращение функции U, возникающее при переходе от точки M к некоторой точке M1 в направлении вектора
. Приращение функции U, возникающее при переходе от точки M к некоторой точке M1 в направлении вектора  определяется как:
определяется как:

или

тогда:

Производной от функции  в точке M по направлению
в точке M по направлению  называется предел:
называется предел:

В общем случае, производная по направлению  характеризует скорость изменения функции (поля) в точке M по этому направлению. При этом возможны два основных случая – производная по направлению может быть как больше нуля, так и соответственно меньше нуля. В первом случае, то есть когда производная по направлению больше нуля:
характеризует скорость изменения функции (поля) в точке M по этому направлению. При этом возможны два основных случая – производная по направлению может быть как больше нуля, так и соответственно меньше нуля. В первом случае, то есть когда производная по направлению больше нуля:

то функция U будет возрастать в направлении  . Если же производная по направлению оказывается меньше нуля, то есть когда:
. Если же производная по направлению оказывается меньше нуля, то есть когда:

то функция U в направлении  будет убывать.
будет убывать.
Кроме того, величина вида:

представляет собой мгновенную скорость изменения функции U в направлении  в точке M. Очевидно, чем больше будет величина последней, тем быстрее будет изменяться функция U. В этом и состоит физический смысл производной по направлению. Выведем формулу для вычисления производной по направлению, считая, что функция
в точке M. Очевидно, чем больше будет величина последней, тем быстрее будет изменяться функция U. В этом и состоит физический смысл производной по направлению. Выведем формулу для вычисления производной по направлению, считая, что функция  дифференцируема в точке M. Составим для этого полное приращение функции
дифференцируема в точке M. Составим для этого полное приращение функции  в точке M, тогда соответственно:
в точке M, тогда соответственно:

учитывая, что:

тогда:

поскольку:

а также:



имеем соответственно:

учитывая, что:

тогда после соответствующих подстановок будем иметь соответственно:

и таким образом:

переходя к пределу отношения  , будем иметь соответственно:
, будем иметь соответственно:

и таким образом приходим к выражению вида:

В случае плоского поля  по определению имеем соответственно:
по определению имеем соответственно:

тогда:

В общем случае, понятие производной по направлению является обобщением частных производных:

которые можно рассматривать как производные от функции U по направлению координатных осей Ox, Oy и Oz. Так, например, если направление  совпадает с положительным направлением оси Ox:
совпадает с положительным направлением оси Ox:

то положив в формуле:

получим:

Для того чтобы установить в каком направлении з всех возможных производная по направлению будет иметь наибольшее значение, вводят понятие градиента функции. Так, нетрудно заметить, что правая часть полученного нами ранее выражения:

представляет собой скалярное произведение единичного вектора:

и некоторого вектора:

Вектор, координатами которого являются значения частных производных функции  в точке
в точке  , называют градиентом функции и обозначают grad U. Отметим, что градиент функции скалярного поля grad U есть векторная величина. Принято говорить, что скалярное поле
, называют градиентом функции и обозначают grad U. Отметим, что градиент функции скалярного поля grad U есть векторная величина. Принято говорить, что скалярное поле  порождает векторное поле градиента:
порождает векторное поле градиента:

или

Теперь, с учётом приведенных нами выше доводов, полученное равенство:

может быть переписано далее в виде:

или
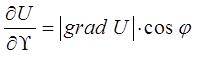
где  – угол между вектором grad U и направлением
– угол между вектором grad U и направлением  .
.

Из формулы
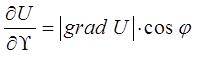
хорошо видно, что производная по направлению достигает наибольшего своего значения, когда  , то есть при
, то есть при  . Таким образом, направление градиента совпадает с направлением
. Таким образом, направление градиента совпадает с направлением  , вдоль которого поле меняется быстрее всего, то есть градиент функции указывает направление наибыстрейшего возрастания функции. Градиент всегда направлен по нормали к поверхности уровня, проходящей через данную точку. Наибольшая скорость изменения функции
, вдоль которого поле меняется быстрее всего, то есть градиент функции указывает направление наибыстрейшего возрастания функции. Градиент всегда направлен по нормали к поверхности уровня, проходящей через данную точку. Наибольшая скорость изменения функции  в точке равна:
в точке равна:
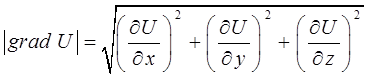
В этом состоит физический смысл градиента. На указанном свойстве градиента основано его широкое применение в математике и других смежных науках. К числу важнейших свойств градиента функции можно отнести следующие из них:
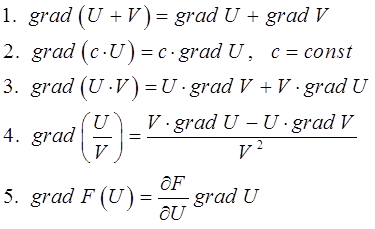
Доказываются эти свойства на основании определения градиента. Однако приведенные выше свойства градиента функции остаются справедливыми и для случая плоского поля. В общем случае, градиент функции скалярного аргумента направлен по нормали к поверхности уровня, проходящей через данную точку.
Действительно, по любому направлению вдоль поверхности уровня  :
:
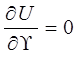
но тогда из выражения:
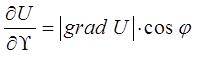
следует, что:

В качестве примера рассмотрим некоторую механическую систему  . Пусть дана поверхность уровня функции:
. Пусть дана поверхность уровня функции:
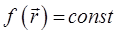
Для потенциальных полей  такую функцию называют эквипотенциальной поверхностью. Тогда градиент
такую функцию называют эквипотенциальной поверхностью. Тогда градиент 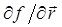 ортогонален поверхности уровня, проходящей через точку
ортогонален поверхности уровня, проходящей через точку 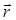 :
:
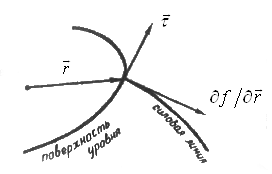
Действительно, возьмём две близко расположенные точки поверхности 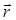 и
и 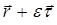 , где
, где  – вектор, касательный к поверхности уровня, а число
– вектор, касательный к поверхности уровня, а число 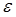 достаточно мало. Разлагая функцию
достаточно мало. Разлагая функцию  в ряд по малой величине
в ряд по малой величине 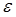 , имеем соответственно:
, имеем соответственно:
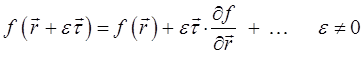
Очевидно, условие:
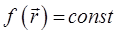
выполняется, если:

Это и есть требование ортогональности градиента и поверхности уровня, так как  принадлежит касательной плоскости поверхности. С градиентом связывают силовую линию, в каждой точке которой градиент
принадлежит касательной плоскости поверхности. С градиентом связывают силовую линию, в каждой точке которой градиент 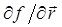 является касательным вектором некоторой кривой. При этом силовые линии, как это хорошо видно из разложения для
является касательным вектором некоторой кривой. При этом силовые линии, как это хорошо видно из разложения для  , будут ортогонально входить в поверхность уровня.
, будут ортогонально входить в поверхность уровня.
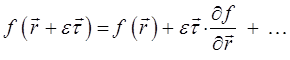
Рассмотрим теперь случай векторного поля, задаваемого некоторым вектором  . В общем случае, изучение поля удобно начинать с понятия векторных линий, поскольку последние являются простейшими геометрическими характеристиками поля. Векторной линией поля
. В общем случае, изучение поля удобно начинать с понятия векторных линий, поскольку последние являются простейшими геометрическими характеристиками поля. Векторной линией поля 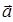 называется линия, касательная к которой в каждой её точке M имеет направление соответствующего й вектора
называется линия, касательная к которой в каждой её точке M имеет направление соответствующего й вектора  . Это понятие для конкретных полей имеет ясный физический смысл. Совокупность всех векторных линий поля, проходящих через некоторую замкнутую кривую, называется векторной трубкой. Изучение векторного поля обычно начинают с изучения расположения его векторных линий. Векторные линии поля:
. Это понятие для конкретных полей имеет ясный физический смысл. Совокупность всех векторных линий поля, проходящих через некоторую замкнутую кривую, называется векторной трубкой. Изучение векторного поля обычно начинают с изучения расположения его векторных линий. Векторные линии поля:

описываются системой дифференциальных уравнений вида:

Действительно, пусть PQ – векторная линия поля и  – её радиус-вектор:
– её радиус-вектор:

тогда, очевидно, вектор  :
:
будет направлен по касательной к линии PQ в точке M. В силу колинеарности векторов  и
и  , следует пропорциональность их проекций, то есть равенства:
, следует пропорциональность их проекций, то есть равенства:

Пусть векторное поле образовано вектором:

Для наглядности будем считать  вектором скорости некоторого потока жидкости, движущейся стационарно. Представим, что некоторая поверхность S находится в этом потоке и пропускает жидкость. Подсчитаем, какое количество жидкости протекает через поверхность S. Для этих целей выберем определённую сторону поверхности S. Пусть
вектором скорости некоторого потока жидкости, движущейся стационарно. Представим, что некоторая поверхность S находится в этом потоке и пропускает жидкость. Подсчитаем, какое количество жидкости протекает через поверхность S. Для этих целей выберем определённую сторону поверхности S. Пусть  – единичный вектор нормали к рассматриваемой стороне поверхности S. Разобьём поверхность на элементарные площадки
– единичный вектор нормали к рассматриваемой стороне поверхности S. Разобьём поверхность на элементарные площадки  . Выберем на каждой площадке некоторую точку
. Выберем на каждой площадке некоторую точку 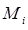 , где
, где 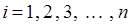 и вычислим значение вектора скорости
и вычислим значение вектора скорости  в каждой точке
в каждой точке 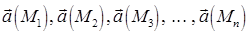 и будем приближённо считать каждую площадку плоской, а вектор
и будем приближённо считать каждую площадку плоской, а вектор 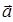 – постоянным по модулю и одинаково направленным в каждой точке площадки. Тогда за единицу времени через
– постоянным по модулю и одинаково направленным в каждой точке площадки. Тогда за единицу времени через 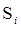 протекает количество жидкости, приближённо равное:
протекает количество жидкости, приближённо равное:
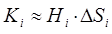
где 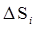 – площадь i-той площадки,
– площадь i-той площадки,  – высота i-го цилиндра образованная
– высота i-го цилиндра образованная  . Учитывая, что
. Учитывая, что  является проекцией вектора
является проекцией вектора 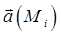 на нормаль
на нормаль  , имеем:
, имеем:
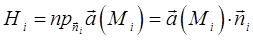
где  – единичный вектор нормали к поверхности в точке
– единичный вектор нормали к поверхности в точке  . Следовательно, общее количество жидкости, протекающее через всю поверхность S за единицу времени, найдём, вычислив сумму:
. Следовательно, общее количество жидкости, протекающее через всю поверхность S за единицу времени, найдём, вычислив сумму:

Точное значение искомого количества жидкости получим, взяв предел найденной суммы при неограниченном увеличении числа элементарных площадок и стремлении к нулю их размеров (диаметров элементарных площадок):


Независимо от изического смысла поля 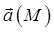 , полученный интеграл называют потоком векторного поля. Потоком вектора
, полученный интеграл называют потоком векторного поля. Потоком вектора  через поверхность S называют интеграл по поверхности от скалярного произведения вектора поля на единичный вектор нормали к поверхности, т.е.
через поверхность S называют интеграл по поверхности от скалярного произведения вектора поля на единичный вектор нормали к поверхности, т.е.
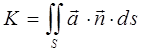
Учитывая в общем случае соотношение вида:

рассмотрим различные формы записи потока вектора. Имеем соответственно:

где  – проекция вектора
– проекция вектора  на направление нормали
на направление нормали 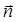 и
и 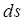 – элемент площади поверхности S. Иногда выражение:
– элемент площади поверхности S. Иногда выражение:
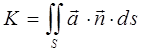
записывают в виде:
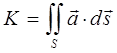
где вектор 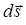 направлен по нормали к поверхности, причём:
направлен по нормали к поверхности, причём:

Поскольку:
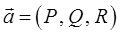
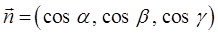
где
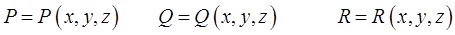
проекции вектора  на соответствующие координатные оси, то поток вектора
на соответствующие координатные оси, то поток вектора  :
:

с учётом приведенных выше соображений, может быть записан в виде:

Как известно из курса анализа, поверхностные интегралы 1-го и 2-го рода связаны между собой соотношением вида:
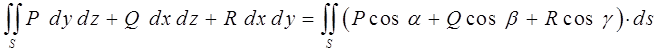
Используя данную взаимосвязь интегрелов, поток вектора можно записать как:

Необходимо также отметить, что поток 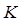 вектора
вектора  есть скалярная величина. Величина
есть скалярная величина. Величина 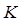 равна объёму жидкости, которая протекает через поверхность S за единицу времени. В этом состоит физический смысл потока вектора, независимо от физического смысла поля. Особый интерес представляет случай, когда поверхность замкнута и ограничивает некоторый объём V. Поток вектора,
равна объёму жидкости, которая протекает через поверхность S за единицу времени. В этом состоит физический смысл потока вектора, независимо от физического смысла поля. Особый интерес представляет случай, когда поверхность замкнута и ограничивает некоторый объём V. Поток вектора,  очевидно, может быть записан в виде:
очевидно, может быть записан в виде:

В ряде случаев поток вектора сквозь замкнутую, ограничивающую некоторый объём поверхность может быть представлен также выражением вида:

В этом случае за направление вектора 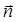 обычно берут направление внешней нормали и говорят о потоке изнутри поверхности S. Если векторное поле
обычно берут направление внешней нормали и говорят о потоке изнутри поверхности S. Если векторное поле 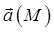 есть поле скоростей текущей жидкости, то величина потока
есть поле скоростей текущей жидкости, то величина потока 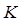 через замкнутую поверхность даёт разность между количеством жидкости, вытекающей из объёма или области V, и втекающем в неё за единицу времени. В точках поверхности S, где векторные линии выходят из объёма V, внешняя нормаль образует с вектором
через замкнутую поверхность даёт разность между количеством жидкости, вытекающей из объёма или области V, и втекающем в неё за единицу времени. В точках поверхности S, где векторные линии выходят из объёма V, внешняя нормаль образует с вектором  острый угол и произведение вектора
острый угол и произведение вектора  и нормали
и нормали 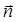 оказываются больше нуля:
оказываются больше нуля:

В точках же, где векторные линии входят в объём, произведение вектора  и нормали
и нормали 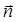 – оказывается меньше нуля:
– оказывается меньше нуля:

При этом если  , то из области V вытекает больше жидкости, чем в неё втекает. Это в свою очередь означает, что внутри области имеются дополнительные источники. И напротив, если
, то из области V вытекает больше жидкости, чем в неё втекает. Это в свою очередь означает, что внутри области имеются дополнительные источники. И напротив, если 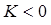 , то внутри области V имеются стоки, поглощающие избыток жидкости. Данные выводы могут быть применены не только к механике, но и электромагнетизму. В таком случае необходимо говорить о собственно источниках и стоках поля. Можно сказать, что источники – точки, откуда векторные линии начинаются, а стоки – точки, где векторные линии кончаются. Так, в электростатическом поле источником являются положительные заряды, в то время как стоками поля являются отрицательные заряды. Если же
, то внутри области V имеются стоки, поглощающие избыток жидкости. Данные выводы могут быть применены не только к механике, но и электромагнетизму. В таком случае необходимо говорить о собственно источниках и стоках поля. Можно сказать, что источники – точки, откуда векторные линии начинаются, а стоки – точки, где векторные линии кончаются. Так, в электростатическом поле источником являются положительные заряды, в то время как стоками поля являются отрицательные заряды. Если же 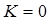 , то из области V вытекает столько же жидкости, сколько в неё втекает в единицу времени; внутри области либо нет ни источников, ни стоков, либо они таковы, что их действие взаимно компенсируется. Важной характеристикой векторного поля является дивергенция, характеризующая распределения и интенсивность источников и стоков поля. Дивергенцией (или расходимостью) векторного поля в точке M:
, то из области V вытекает столько же жидкости, сколько в неё втекает в единицу времени; внутри области либо нет ни источников, ни стоков, либо они таковы, что их действие взаимно компенсируется. Важной характеристикой векторного поля является дивергенция, характеризующая распределения и интенсивность источников и стоков поля. Дивергенцией (или расходимостью) векторного поля в точке M:

называется скаляр вида:

и обозначается символом div  , т.е.
, т.е.

Отметим некоторые основные свойства дивергенции:

эти свойства легко проверить, используя формулу:

Используя понятия потока и дивергенции векторного поля, можно теперь будет записать хорошо известную из анализа формулу Остроградского – Гаусса в так называемой векторной форме. Итак, будем иметь соответственно:

Действительно, рассматривая область V, ограниченную замкнутой поверхностью S, в векторном поле:

можно утверждать, что левая часть выражения:

есть поток вектора  через поверхность S. В справедливости такого рода утверждений можно легко убедиться, если вспомнить что:
через поверхность S. В справедливости такого рода утверждений можно легко убедиться, если вспомнить что:


а также:
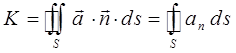
тогда соответственно:
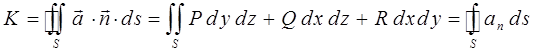
или
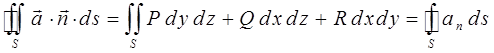
Для нашего случая:

Анализ левой части формулы Остроградского – Гаусса:

показывает, что:
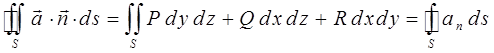
и таким образом:
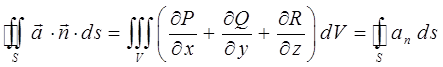
Анализ правой части данного выражения:
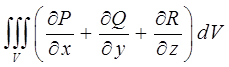
с учётом приведенных выше соображений:

приводит соответственно к выражению:

Таким образом, в ходе приведенных выкладок, формула Остроградского – Гаусса
распадается на два тождественных выражения, в совокупности сводящих векторную форму записи данного уравнения к её аналогу – дифференциальной форме записи данного уравнения. Итак, имеем соответственно:

Данное уравнение, записанное в так называемой векторной форме, в ходе проделанных выкладок распадается на два уравнения:
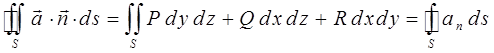
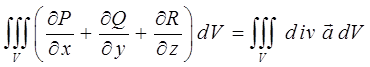
Поскольку левые части данных уравнений равны между собой, то, следовательно, будут равны и их правые части:

или что тоже самое:

Данные уравнения в терминах строгого формализма могут быть также переписаны и в несколько иной форме:

или учитывая, что  , можно записать:
, можно записать:

Полученное выражение, также является уравнением Остроградского – Гаусса, но записанное теперь уже в дифференциальной форме. Формула Остроградского – Гаусса в общем случае означает, что поток векторного поля через замкнутую поверхность S (в направлении внешней нормали, то есть изнутри) равен тройному интегралу от дивергенции этого поля по объёму V, ограниченному данной поверхностью. На основании формулы вида:

Можно дать также и другое определение дивергенции векторного поля  в точке M и не связанное с выбором координатных осей. Так, на основании теоремы о среднем для тройного интеграла имеем:
в точке M и не связанное с выбором координатных осей. Так, на основании теоремы о среднем для тройного интеграла имеем:

где 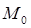 – некоторая (средняя) точка области V. Тогда полученные нами выражения:
– некоторая (средняя) точка области V. Тогда полученные нами выражения:
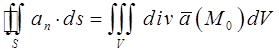
или

можно будет представить далее к виду:

или
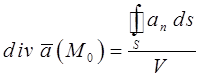
Пусть поверхность S стягивается в точку, тогда  ,
,  и мы получаем выражение для div
и мы получаем выражение для div  в точке M:
в точке M:
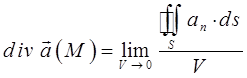
или

Дивергенцией векторного поля в точке M называется предел отношения потока поля через замкнутую поверхность S, окружающую точку M, к объёму тела, ограниченного этой поверхностью, при условии, что вся поверхность стягивается в точку M, при условии, что  . Указанное выше определение дивергенции эквивалентно данному в начале определению. Как видно из определения, дивергенция векторного поля в точке является скалярной величиной. Она образует скалярное поле в данном векторном поле. Исходя из физического смысла потока вектора, можно сказать, что: при
. Указанное выше определение дивергенции эквивалентно данному в начале определению. Как видно из определения, дивергенция векторного поля в точке является скалярной величиной. Она образует скалярное поле в данном векторном поле. Исходя из физического смысла потока вектора, можно сказать, что: при  точка M представляет собой источник, откуда жидкость вытекает; при
точка M представляет собой источник, откуда жидкость вытекает; при 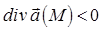 точка M представляет собой сток, поглощающий жидкость. Как правило, условно считается, что
точка M представляет собой сток, поглощающий жидкость. Как правило, условно считается, что 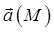 есть поле скоростей фиктивного стационарного потока несжимаемой жидкости. Как это следует из выражения для дивергенции векторного поля, выражающего эквивалентную формулировку данного понятия, величина div
есть поле скоростей фиктивного стационарного потока несжимаемой жидкости. Как это следует из выражения для дивергенции векторного поля, выражающего эквивалентную формулировку данного понятия, величина div  характеризует мощность (плотность, интенсивность) источника или стока в точке M. В этом состоит физический смысл дивергенции. Понятно, что если в объёме V, ограниченном замкнутой поверхностью S, нет ни источников, ни стоков, тогда:
характеризует мощность (плотность, интенсивность) источника или стока в точке M. В этом состоит физический смысл дивергенции. Понятно, что если в объёме V, ограниченном замкнутой поверхностью S, нет ни источников, ни стоков, тогда:

Векторное поле, в каждой точке которого дивергенция поля div  равна нулю, называется соленоидальным или трубчатым. Введём теперь представления о циркуляции векторного поля. Итак, пусть векторное поле образовано вектором:
равна нулю, называется соленоидальным или трубчатым. Введём теперь представления о циркуляции векторного поля. Итак, пусть векторное поле образовано вектором:

Возьмём в этом поле некоторую замкнутую кривую L и выберем на ней некоторое направлении. Пусть  – радиус-вектор точки M на контуре L. Задавая векторы трёхмерного пространства не только тройкой компонент, но и явным разложением по ортам координатных осей, будем иметь соответственно:
– радиус-вектор точки M на контуре L. Задавая векторы трёхмерного пространства не только тройкой компонент, но и явным разложением по ортам координатных осей, будем иметь соответственно:

Известно, что вектор  направлен по касательной к кривой в направлении её обхода и
направлен по касательной к кривой в направлении её обхода и  , где
, где 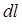 – дифференциал дуги рассматриваемой кривой L, тогда:
– дифференциал дуги рассматриваемой кривой L, тогда:
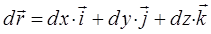
и соответственно:
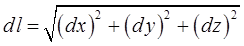
Криволинейный интеграл по замкнутому контуру L от скалярного произведения вектора 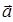 на вектор
на вектор  , касательный к контуру L, называется циркуляцией вектора вдоль контура L, т.е.
, касательный к контуру L, называется циркуляцией вектора вдоль контура L, т.е.
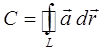
Рассмотрим различные формы записи для циркуляции. Так, учитывая, что:

тогда выражение:
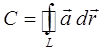
может быть переписано в виде:

или
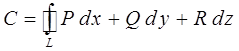
здесь  – проекция вектора
– проекция вектора  на касательную τ, проведенную в направлении обхода кривой L. Циркуляция С, записанная в таком виде имеет простой физический смысл – это работа силы
на касательную τ, проведенную в направлении обхода кривой L. Циркуляция С, записанная в таком виде имеет простой физический смысл – это работа силы 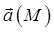 векторного поля при перемещении материальной точки M, вдоль некоторой кривой L. Необходимо отметить, что вдоль замкнутых векторных линий циркуляция вектора
векторного поля при перемещении материальной точки M, вдоль некоторой кривой L. Необходимо отметить, что вдоль замкнутых векторных линий циркуляция вектора 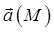 отлична от нуля, поскольку в каждой точке векторной линии скалярное произведение
отлична от нуля, поскольку в каждой точке векторной линии скалярное произведение 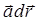 сохраняет свой знак: положительный, если направление вектора
сохраняет свой знак: положительный, если направление вектора  совпадает с направлением обхода векторной линии и отрицательный, если направление обхода векторной линии не совпадает с направлением вектора
совпадает с направлением обхода векторной линии и отрицательный, если направление обхода векторной линии не совпадает с направлением вектора  . Следующим важным понятием теории поля, является понятие ротора (или вихря) векторного поля, определяемого некоторым вектором
. Следующим важным понятием теории поля, является понятие ротора (или вихря) векторного поля, определяемого некоторым вектором  . В общем случае, ротором (или вихрем):
. В общем случае, ротором (или вихрем):

называется вектор, обозначаемый 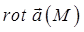 и определяемый формулой:
и определяемый формулой:
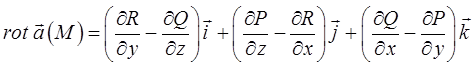
полученное выражение можно записать также с помощью определителя:
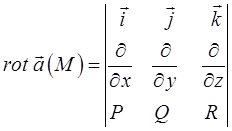
Отметим некоторые свойства ротора:

Эти свойства легко проверить, используя формулу:
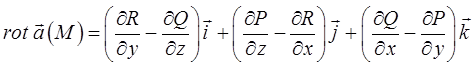
Используя понятие ротора и циркуляции вектора  векторного поля, запишем известную в анализе формулу Стокса:
векторного поля, запишем известную в анализе формулу Стокса:
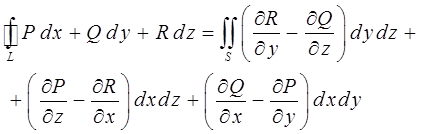
При внимательном рассмотрении данного выражения легко заметить, что левая часть формулы представляет собой циркуляцию вектора  по контуру L:
по контуру L:
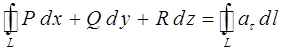
Интеграл же в правой части данного выражения представляет собой поток вектора  через поверхность S, ограниченную контуром L, т.е.
через поверхность S, ограниченную контуром L, т.е.
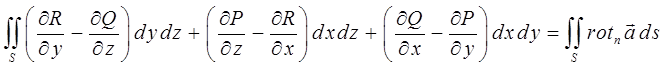
следовательно, формулу Стокса можно записать в виде:

Такое представление формулы Стокса называют также её векторной формой. Здесь положительное направление на контуре L и выбор стороны у поверхности S согласованы между собой также, как в теореме Стокса. Полученное нами выше выражение показывает, что циркуляция вектора  вдоль замкнутого контура L равна потоку ротора этого вектора
вдоль замкнутого контура L равна потоку ротора этого вектора  через поверхность S, лежащую в поле вектора
через поверхность S, лежащую в поле вектора  и ограниченную контуром L (натянутую на контур):
и ограниченную контуром L (натянутую на контур):

используя полученную нами уже ранее формулу:
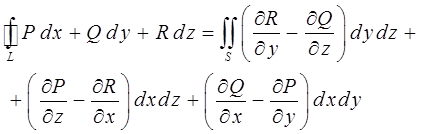
можно дать другое определение ротора поля, эквивалентное первому и не зависящее от выбора системы координат. Для этого применим формулу Стокса для достаточно малой плоской площадки S с контуром L, содержащей точку M. Имеем соответственно:

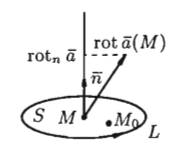
На основании теоремы о среднем для поверхностного интеграла, имеем:
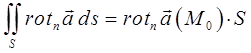
где 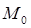 – некоторая средняя точка площадки S. Тогда формулу:
– некоторая средняя точка площадки S. Тогда формулу:

с учётом выражения:
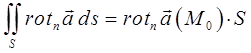
можно переписать в виде:

или

отсюда:

Пусть контур L стягивается в точку M, тогда соответственно  , а
, а 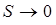 или, переходя к пределу, получаем выражение для
или, переходя к пределу, получаем выражение для  в точке M:
в точке M:

откуда будем иметь соответственно выражение:

Таким образом, ротором вектора  в точке M называется вектор, проекция которого на каждое пространственное направление равна пределу отношения циркуляции вектора
в точке M называется вектор, проекция которого на каждое пространственное направление равна пределу отношения циркуляции вектора  по контуру L плоской площадки S, перпендикулярной этому направлению, к площади этой площадки. Ротор вектора
по контуру L плоской площадки S, перпендикулярной этому направлению, к площади этой площадки. Ротор вектора  есть векторная величина, образующая собственное векторное поле. Из определения для ротора
есть векторная величина, образующая собственное векторное поле. Из определения для ротора  , вытекает в свою очередь, что направление ротора – это направление, вокруг которого циркуляция имеет наибольшее значение (плотность) по сравнению с циркуляцией вокруг любого другого направления, не совпадающего с нормалью к площадке S. По этой причине связь между ротором и циркуляцией аналогична связи градиента с производной по направлению. Познакомимся теперь с так называемыми дифференциальными операциями 1-го и 2-го порядка. К такого рода операциям над скалярными U и векторными
, вытекает в свою очередь, что направление ротора – это направление, вокруг которого циркуляция имеет наибольшее значение (плотность) по сравнению с циркуляцией вокруг любого другого направления, не совпадающего с нормалью к площадке S. По этой причине связь между ротором и циркуляцией аналогична связи градиента с производной по направлению. Познакомимся теперь с так называемыми дифференциальными операциями 1-го и 2-го порядка. К такого рода операциям над скалярными U и векторными  полями являются взятие
полями являются взятие  ,
, 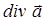 и
и  . Такого рода операции называются векторными операциями первого порядка, поскольку в них участвуют только первые производные. Эти операции удобно записывать, используя выражение:
. Такого рода операции называются векторными операциями первого порядка, поскольку в них участвуют только первые производные. Эти операции удобно записывать, используя выражение:

называемое также оператором Гамильтона. Символическое «умножение» вектора ∇ на скаляр или вектор  производится по обычным правилам линейной алгебры, а умножение производных на соответствующие величины U, P, Q, R понимают как взятие соответствующих производных от этих величин. При этом сам оператор действует только на конкретный множитель, расположенный непосредственно за оператором. Таким образом, имеем соответственно:
производится по обычным правилам линейной алгебры, а умножение производных на соответствующие величины U, P, Q, R понимают как взятие соответствующих производных от этих величин. При этом сам оператор действует только на конкретный множитель, расположенный непосредственно за оператором. Таким образом, имеем соответственно:
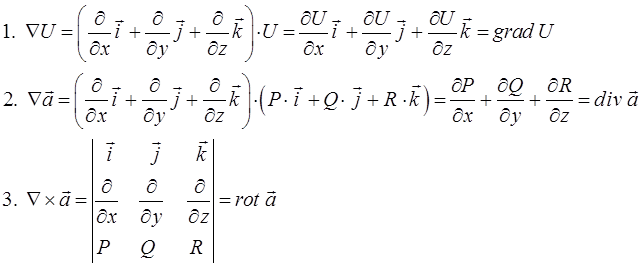
Применение оператора Гамильтона к скалярному или векторному полю порождает новое поле, к которому можно снова применить этот оператор. В результате можно получить так называемые дифференциальные операции второго порядка. Как и в предыдущем случае символическое «умножение» вектора ∇ на скаляр или вектор  производится по обычным правилам линейной алгебры, а умножение производных на соответствующие величины U, P, Q, R понимают как взятие соответствующих производных от этих величин. При этом сам оператор действует только на конкретный множитель, расположенный непосредственно за оператором. Таким образом, имеем соответственно:
производится по обычным правилам линейной алгебры, а умножение производных на соответствующие величины U, P, Q, R понимают как взятие соответствующих производных от этих величин. При этом сам оператор действует только на конкретный множитель, расположенный непосредственно за оператором. Таким образом, имеем соответственно:

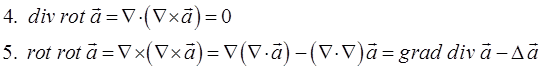
Перейдём теперь к рассмотрению особого класса полей, называемых также ещё потенциальными. Ранее, при рассмотрении градиента скалярной функции мы уже затрагивали вопросы касающиеся такого рода полей. Вернёмся теперь к их рассмотрению, только уже с позиций введных выше представлений. В общем случае, векторное поле  называется потенциальным (безвихревым или градиентным), если во всех точках поля, ротор поля равен нулю, то есть при условии, что:
называется потенциальным (безвихревым или градиентным), если во всех точках поля, ротор поля равен нулю, то есть при условии, что:

Потенциальное векторное поле можно представить как градиент некоторой скалярной функции координат (потенциала). Необходимым условием потенциальности векторного поля является равенство нулю ротора поля. Однако это условие не является достаточным. В физике, имеющей дело с силовыми полями, математическое условие потенциальности силового поля можно представить как требование равенства нулю работы по перемещению частицы, на которую действует поле, по замкнутому контуру. Этот контур не обязательно должен быть траекторией движения частицы, движущейся под действием этих сил. В качестве потенциала поля в этом случае можно выбрать работу по перемещению частицы из некоторой произвольно выбранной исходной точки в заданную точку и эта работа по определению не зависит от пути перемещения. Например, потенциальными являются статическое электрическое поле, а также гравитационное поле. На языке дифференциальных форм потенциальное поле – это точная 1-форма, то есть форма, которая является внешним дифференциалом 0-формы (функции). Градиенту соответствует взятие внешнего дифференциала от 0-формы (потенциала), ротору же соответствует взятие внешнего дифференциала от 1-формы (поля). Необходимое условие следует из того, что второй внешний дифференциал всегда равен нулю. Интегральные формулы, в общем случае, следуют из обобщённой теоремы Стокса. Примером потенциального поля является электрическое поле напряжённости точечного заряда. Потенциальное поле, в общем случае, обладает следующими основными свойствами:
Свойство 1: Циркуляция потенциального поля  по любому замкнутому контуру в этом поле равна нулю:
по любому замкнутому контуру в этом поле равна нулю:

в частности, для силового потенциального поля это означает, что работа силы по любому замкнутому контуру равна нулю. В поле скоростей текущей жидкости равенство  означает, что в потоке нет замкнутых струек, т.е. нет водоворотов.
означает, что в потоке нет замкнутых струек, т.е. нет водоворотов.
Свойство 2: В потенциальном поле  криволинейный интеграл вида:
криволинейный интеграл вида:

вдоль любой кривой L с началом в точке  и концом в точке
и концом в точке  зависит только от положения точек
зависит только от положения точек  и
и  , и не зависит от формы кривой. Это свойство вытекает из предыдущего, первого свойства. Действительно, взяв в поле две точки
, и не зависит от формы кривой. Это свойство вытекает из предыдущего, первого свойства. Действительно, взяв в поле две точки  и
и  , соединим их двумя кривыми
, соединим их двумя кривыми  и
и  так, чтобы полученный контур
так, чтобы полученный контур  лежал внутри поля. В силу предыдущего свойства, а также учитывая свойства самого криволинейного интеграла, имеем соответственно:
лежал внутри поля. В силу предыдущего свойства, а также учитывая свойства самого криволинейного интеграла, имеем соответственно:
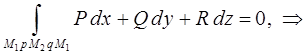

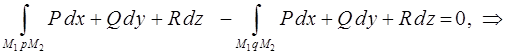

Свойство 3: Потенциальное поле является полем градиента некоторой скалярной функции 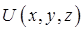 , т.е. если
, т.е. если 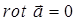 , то существует функция
, то существует функция 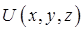 такая, что
такая, что 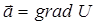 . Из равенства
. Из равенства  вытекает, что:
вытекает, что:
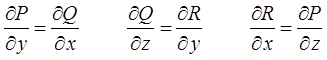
то есть выражение:

является полным дифференциалом некоторой функции 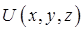 . Эту функцию называют потенциалом векторного поля
. Эту функцию называют потенциалом векторного поля  :
:
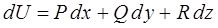
откуда:
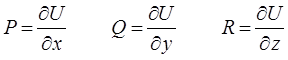
следовательно:

то есть вектор поля  является градиентом скалярного поля. Из равенства вида:
является градиентом скалярного поля. Из равенства вида:
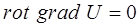
следует также обратное утверждение – поле градиента некоторой скалярной функции 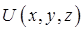 является потенциальным. Из равенства
является потенциальным. Из равенства 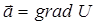 следует, в свою очередь, что потенциальное поле определяется заданием одной скалярной функции
следует, в свою очередь, что потенциальное поле определяется заданием одной скалярной функции 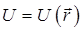 – его потенциала. Определение потенциального поля может быть дано иначе – векторное поле
– его потенциала. Определение потенциального поля может быть дано иначе – векторное поле  называется потенциальным, если оно является градиентом некоторого скалярного поля, то есть если
называется потенциальным, если оно является градиентом некоторого скалярного поля, то есть если 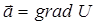 .
.
Учитывая, что векторные линии в общем случае направлены в сторону убывания потенциала U, данное выражение можно переписать, представив к виду:
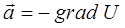
Так, поток жидкости направлен туда, где давление этой жидкости меньше; теплота перемещается от более нагретого места к менее нагретому месту. Построим новую функцию координат так, чтобы соответствующие ей силовые линии совпадали с механическими траекториями. Такая функция называется действием и обозначается через 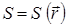 . Градиент
. Градиент  с точностью до множителя должен совпадать с касательным вектором траектории, т.е. с вектором скорости
с точностью до множителя должен совпадать с касательным вектором траектории, т.е. с вектором скорости  . Но поскольку импульс
. Но поскольку импульс  имеет более фундаментальное значение, то величина действия S вводится требованием:
имеет более фундаментальное значение, то величина действия S вводится требованием:
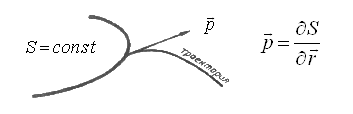
Из выше изложенного становится очевидным, что траектории будут ортогонально входить в поверхность постоянного действия. Чтобы уяснить смысл S, рассмотрим одномерный случай (одна степень свободы), при которой  , а также что:
, а также что:

откуда имеем соответственно:

Интегрирование последнего выражения даёт:
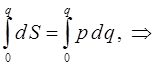
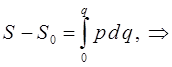
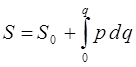
видно, что величина действия S имеет размерность [энергия]×[время]:
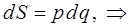

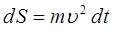
Полная энергия в одномерном случае:

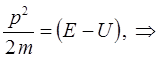

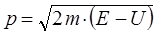
принимая в выражении:
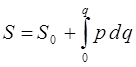
несущественную константу интегрирования  , находим после подстановки:
, находим после подстановки:

В общем случае 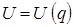 . Для свободного движения, когда потенциальное поле отсутствует
. Для свободного движения, когда потенциальное поле отсутствует 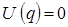 , имеем:
, имеем:
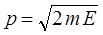
и соответственно величина действия для свободной частицы:

В общем случае для n степеней свободы полагаем:

тогда соответственно:

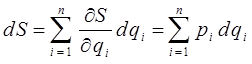
и действие вычисляется в виде криволинейного интеграла:

в трёхмерном случае:

в декартовых переменных это равнозначно: