Анализ однородных открытых СеМО. Теорема Джексона

 

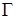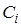Определим сеть массового обслуживания , состоящую из систем массового обслуживания типа 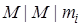, , обслуживающих требования одного класса, поступающие из внешнего источника 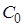. Переходы требований между системами обслуживания сети определяются неприводимой маршрутной матрицей 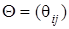, . Входящий в сеть обслуживания поток требований пуассоновский с интенсивностью 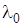. Система 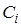, , содержит 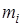параллельно работающих одинаковых приборов, длительность обслуживания требований прибором имеет экспоненциальное распределение с параметром 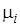. Выбор в системе 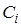очередного требования на обслуживание производится из общей очереди неограниченной длины согласно дисциплине .

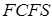Введем обозначения:

– вектор состояния сети 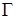, где – число требований, пребывающих в системе , , ;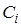

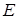– множество всех состояний сети;

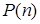– стационарная вероятность пребывания сети 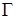в состоянии ;

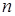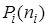– стационарная вероятность пребывания системы 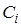в состоянии ;

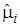– суммарная интенсивность обслуживания требований системой 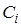, т. е. среднее число требований, обслуживаемых в единицу времени, когда приборы системы непрерывно заняты, ;

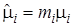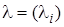– вектор интенсивностей потоков требований, ,

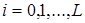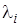– интенсивность входящего (и выходящего) потока требований в систему ;

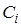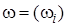– вектор относительных интенсивностей потоков требований, ,

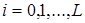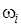– относительная интенсивность потока требований в систему ;

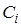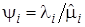– коэффициент использования системы .

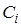Теорема Джексона. Если для однородной открытой сети массового обслуживания 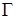выполнены условия:

1) все входящие в сеть потоки пуассоновские;

2) все переходы требований между системами в сети определяются маршрутной матрицей;

3) все длительности обслуживания требований имеют экспоненциальное распределение, причем интенсивность обслуживания может зависеть от числа требований в системе;

4) дисциплина выбора требований из очереди в каждой системе не зависит от длительности обслуживания и маршрутов требований, то каждая система 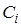, , функционирует как независимая в вероятностном смысле система массового обслуживания, и стационарные вероятности состояний сети имеют вид

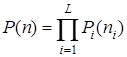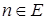, , (1)

где

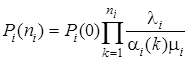(2)

суть стационарные вероятности состояний систем 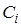типа 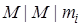, рассматриваемых как взаимно независимые с пуассоновскими входящими потоками с интенсивностями 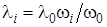, а .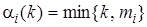

Доказательство. Если в момент 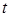сеть находится в состоянии 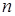, то за интервал времени 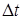могут произойти следующие события:

1) не произойдет никаких изменений;

2) в систему 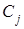поступит требование из источника;

3) после завершения обслуживания в системе 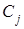требование покинет сеть обслуживания (перейдет в источник);

4) после завершения обслуживания в системе 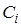требование поступит в систему .

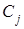Вероятность других событий равна .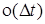

Для учета только доступных переходов введем вспомогательную функцию

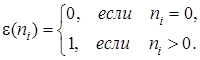
Для упрощения записи уравнений равновесия обозначим

.

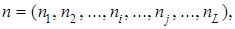
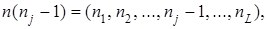
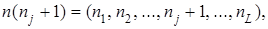
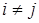Тогда уравнения равновесия можно записать в виде

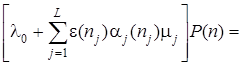
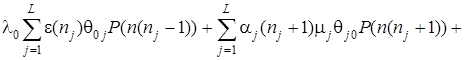
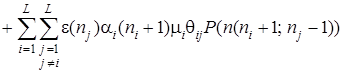. (3)

Левая часть уравнения (3) представляет собой стационарную вероятность состояния 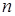, умноженную на суммарную интенсивность выхода из этого состояния.

Правая часть содержит по одному слагаемому для каждого состояния, из которого можно попасть в состояние 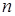за один переход. Каждое из этих слагаемых представляет собой произведение соответствующей вероятности состояния на интенсивность перехода из него в .

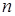Покажем, что подстановка выражений (1) и (2) в уравнение (3) обращает (3) в тождество. Действительно, каждое слагаемое в обеих частях равенства будет содержать множитель 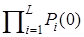, на который можно сократить. Чтобы установить равенство слагаемых в левой и правой частях уравнения (3), выделим в каждом слагаемом в правой части коэффициент 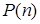. Из соотношений (2) и (3) следует

,

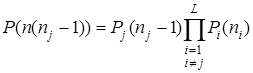где

.

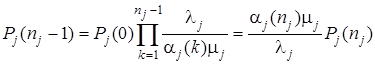Следовательно

.

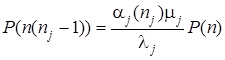Аналогично

,

.

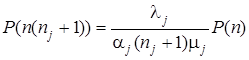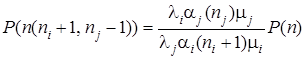Подставляя эти выражения в (3) и сократив на 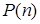, получим

.

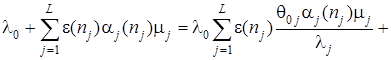
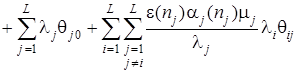Это равенство обращается в тождество, учитывая, что

, .

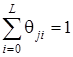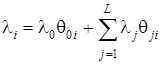Таким образом, теорема доказана.

Теорема Джексона обеспечивает возможность построения метода анализа открытой сети обслуживания, основанного на композиции известных расчетных формул для систем обслуживания 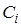типа :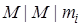

,

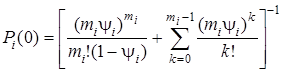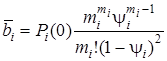– математическое ожидание (м.о.) числа требований в очереди системы ,

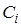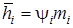– м.о. числа занятых приборов системы ,

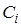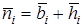– м.о. числа требований в системе ,

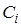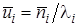– м.о. длительности пребывания требований в системе .

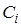Алгоритм, реализующий метод анализа однородных открытых экспоненциальных СеМО:

1) решение системы уравнений с условием нормировки ;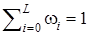

2) вычисление , ;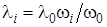

3) проверка условия существования стационарного режима , ;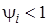

4) вычисление стационарных характеристик 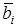, , , .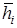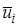