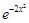ЗАДАЧА № 2
Выразить событие С через события Аi или Аi и Bj из условия задачи, используя операции сложения, умножения и отрицания. При этом слагаемые в выражении должны быть попарно несовместны.
1. Игральная кость брошена четыре раза. Аi - при i-м бросании выпала цифра 6. С - цифра 6 при всех бросаниях выпала не менее трех раз.
2.
| |
 |
Аi - i-й элемент исправен. С - цепь не пропускает ток.
3. Два стрелка стреляют по очереди, но не более трех раз каждый. Победителем считается стрелок, который попадает в мишень первым.
Аi - первый стрелок попал при i-м выстреле.
Bj - второй стрелок попал при j-м выстреле.
С- победил первый стрелок.
4. У мальчика имеются деньги на шесть выстрелов в тире. Он купил три патрона и решил, что купит затем еще два, если ни разу не промахнется. Последний выстрел он решил себе позволить, если перед этим не промахнулся ни разу.
Аi - мальчик попал при i-м выстреле.
С - мальчик потратил не все свои деньги.
5. Электрическая цепь содержит 4 элемента и составлена по схеме
 |
Аi- i-й элемент вышел из строя. С - цепь пропускает ток.
6. Для контроля качества из партии изделий отбирается три экземпляра. Они проходят внешний осмотр, и вся партия принимается, если дефектов нет. Если все три изделия имеют дефект, то партия признается негодной. В других случаях проводится дополнительная проверка изделий на работоспособность, а партия признается годной, если все изделия эту проверку выдержали.
Аi - i-я деталь не имеет внешних дефектов.
Вj- j-я деталь выдержала дополнительную проверку.
С - партия признана годной.
7. Стрелок выстрелил по мишени четыре раза. Аi- стрелок попал при i-м выстреле. С – общее число попаданий четно.
8. Стрелок дважды стреляет по мишени. Если он попадает хоть один раз, то ему затем выдают патроны до первого промаха.
Аi - стрелок попал при i-м выстреле.
С - израсходовано не менее пяти патронов.
9. У каждого из двух игроков имеются белые и черные шары. Они дважды берут по одному из своих шаров и обмениваются ими.
Аi- первый игрок при i-м обмене отдал белый шар.
BJ - второй игрок при j-м обмене отдал белый шар.
С- количество белых шаров у первого игрока после обменов увеличилось.
10. Из пяти деталей выбирают одну годную, проверяя их последовательно.
Аi - i-я выбранная деталь годная.
С -годная деталь нашлась раньше, чем были проверены все детали.
11. Прибор содержит две детали первого типа и три второго типа. Прибор работает, если среди деталей каждого типа не более одной негодной.
Аi - i-я деталь первого типа исправна.
BJ - j-я деталь второго типа исправна.
С- прибор работает.
12. Цепь содержит пять элементов и составлена по схеме
 |
Аi- i-й элемент исправен. С - Цепь пропускает ток.
13. Проверено три детали первого типа и две детали второго типа.
Аi - i-я деталь первого типа исправна.
BJ - j-я деталь второго типа исправна.
С - исправных деталей первого типа на две больше, чем годных деталей второго типа.
14. Из колоды последовательно извлечено пять карт.
Аi - i-я карта является тузом.
С - всего извлечено не белее одного туза.
15. Для сдачи экзамена студент должен выполнить два обязательных задания. После этого ему дается еще два дополнительных задания, из которых необходимо выполнить хотя бы одно.
Аi– i-е обязательное задание выполнено.
BJ - j-е дополнительное задание выполнено.
С- экзамен не сдан.
16.
| |
 |
Аi- i-й элемент исправен. С - цепь пропускает ток.
17. Два стрелка по очереди стреляют по мишени по два раза.
Аi- первый стрелок попал при i-м выстреле.
BJ - второй стрелок попал при j-м выстреле.
С- стрелки попали в мишень равное число раз.
18. Два шахматиста играют матч из трех партий.
Аi – i-ю партию выиграл первый шахматист.
BJ - j-я партия закончилась вничью.
С - матч выиграл первый шахматист.
19. Электрическая цепь содержит четыре элемента и соединена по схеме
 |
Аi-– i-й элемент исправен. С- цепь пропускает ток.
20. У мальчика имеются деньги для оплаты шести выстрелов в тире. Он решил покупать по два патрона, причем каждую следующую пару покупать, если перед этим не промахнулся.
Аi - мальчик попал при i-м выстреле.
С - мальчик не истратил все свои деньги.
21. У ребят имеется семь монет, которые они решили истратить на газированную воду. Автомат барахлит, и как только он глотает монету, не наливая воды, они прекращают свое занятие.
Аi - автомат налил воды при бросании i-й монеты.
С- у ребят после питья осталось еще нечетное число монет.
22. Цепь содержит четыре элемента и соединена по схеме
 |
Аi – i-й элемент исправен. С- цепь не пропускает ток.
23. Два стрелка стреляют по мишени по два раза каждый.
Аi - первый стрелок попал при i-м выстреле.
BJ - второй стрелок попал при j -м выстреле.
С - второй стрелок попал в мишень на один раз больше первого.
24. Игральная кость бросается четыре раза. Аi -при i-м бросании выпало четное число. С- сумма выпавших чисел нечетна.
25. Два игрока бьют мячом по воротам по три раза каждый.
Аi- первый игрок забил мяч при i-м ударе.
BJ - второй игрок забил мяч при j-м ударе.
С- второй игрок забил, по крайней мере, на два мяча больше, чем первый.
26. Из урны с черными и белыми шарами последовательно извлекается четыре шара. Аi - i -й шар черный. С - всего белых шаров извлечено больше, чем черных.
27. Экзаменующемуся выдается билет с тремя вопросами. Если он не знает ни один вопрос, то ему ставится неудовлетворительная оценка. Если он знает все вопросы, ставится "отлично". В других случаях задается два дополнительных вопроса и оценка "хорошо" ставится, если экзаменующийся знает их оба.
Аi - студент знает i-й вопрос из билета.
BJ - студент знает j -й дополнительный вопрос.
С - экзаменующийся сдал экзамен на "хорошо" или "отлично".
28. Для изготовления нужной детали ученику выдано 6 заготовок, которые он обрабатывает одну за другой. Аi - i-я заготовка испорчена.
С- ученик использовал не более половины заготовок для изготовления детали.
29. Электрическая цепь содержит 5 элементов и соединена по схеме

Аi - i -й элемент исправен. С - цепь пропускает ток.
30. Из урны с белыми, черными и красными шарами игрок достает два шара. Если они оба белые, то игра прекращается. В противном случае ему разрешают взять следующий пар, а если он красный, то игрок берет еще один шар.
Аi - i-й извлеченный шар белый.
BJ - j-й извлеченный шар красный.
С - в результате игры игрок извлек два белый шара.
ЗАДАЧА № 3
1. На пяти карточках написаны числе 1,2,3,4,5. Наудачу берут две карточки. Найти вероятность того, что большее из извлеченных чисел равно 4.
2. В лифт шестиэтажного дома на первом этаже вошло 4 человека. Каждый из них с одинаковой вероятностью выходит на любом из этажей, начиная со второго. Какова вероятность, что трое выйдут на одном этаже?
3. В коробке 10 красный, 6 зеленых и 8 синих карандашей. Три из них вынимаются наугад. Найти вероятность того, что все карандаши разных цветов.
4. Наудачу выбирается шестизначное число. Какова вероятность того, что число одинаково читается как слева направо, так и справа налево (например, 123321)?
5. Бросаются одновременно три игральные кости. Найти вероятность того, что сумма выпавших очков кратна 5.
6. Из полного комплекта домино извлекается наудачу одна кость. Чему равна вероятность того, что сумма очков на обеих половинках этой кости окажется равной 7?
7. Ребенок, играя с карточками, на которых написаны буквы латинского алфавита (26 карточек), случайным образом выбирает 6 карточек. Найти вероятность того, что из букв, написанных на них, можно составить слово "BEGIN ".
8. Найти вероятность того, что 7 случайно выбранных человек родились в разные дни недели.
9. Выполняя заказ на изготовление 50 золотых медалей, ювелир заменил 2 медали на фальшивые. Для контроля заказчик случайным образом выбирает три медали. Какова вероятность разоблачения ювелира?
10. Наудачу выбирается семизначное число. Найти вероятность того, что число одинаково читается как слева направо, так и справа налево (например, 4321234).
11. Рассеянная студентка написала письма 5 подругам, запечатала в конверты и обнаружила, что забыла написать адреса получателей. Какова вероятность того, что "свои" письма получат в точности три подруги, если адреса на конвертах будут написаны на удачу?
12. На столе экзаменатора 25 занумерованных экзаменационных билетов. Два студента по очереди берут по одному билету. Найти вероятность того, что меньший номер у выбранных билетов равен 7.
13. Ребёнок, играя с карточками, на которых написаны буквы латинского алфавита (26 карточек), случайным образом выбирает 4 карточки. Какова вероятность того, что из букв, написанных на них, можно составить слово “READ”?
14. Каждый из 5 шаров случайным образом кладут в один из 6 ящиков. Какова вероятность, что все шары попадут в разные ящики?
15. У радиомонтажника имеется 20 микросхем, 15 из них выпущены в мае, а 5 - в июне. Радиомонтажник наугад выбирает 10 микросхем и устанавливает в прибор. Найти вероятность того, что в приборе окажутся 6 микросхем, выпущенных в мае, и 4- в июне.
16. 10 человек входят в комнату, где имеется всего 8 стульев, и рассаживаются случайным образом, но так, что все стулья оказываются занятыми. Какова вероятность того, что два определенных человека останутся без места?
17. Среди кандидатов в сборную команду института 3 первокурсника, 4- второкурсника и 7 третьекурсников. Для участия в соревнованиях формируется сборная из 5 человек. Какова вероятность того, что в сборной не окажется второкурсников, если отбор в сборную производится случайным образом?
18. В лифт 7-этажного дома на первом этаже вошли 6 пассажиров. Какова вероятность того, что четверо выйдут на одном этаже, если каждый из пассажиров с одинаковой вероятностью выходит на любом из этажей, начиная со второго?
19. В лотерее разыгрывается 6 ценных подарков. Найти вероятность того, что среди 4 наудачу взятых билетов окажется 2 «счастливых», если всего было выпущено 50 билетов.
20. 8 вариантов контрольной работы, написанных каждый на отдельной карточке, перемешиваются и распределяются случайным образом среди 6 студентов, сидящих за круглым столом, причем каждый получает по одному варианту. Найти вероятность, что варианты 1 и 2 достанутся рядом сидящим.
21. 7 шаров случайным образом кладут в 7 ящиков. Какова вероятность, что в каждом ящике окажется по одному шару?
22. Ребенок, играя с карточками, на которых напечатаны буквы русского алфавита (33 карточки), выбирает 5 карточек. Какова вероятность того, что из букв, написанных на них, можно составить слово "ИГРА" ?
23. Для выборочного анкетирования случайным образом отбирают 5 человек из группы, в которой 8 девушек и 16 юношей. Найти вероятность того, что среди отобранных 3 юношей и 2 девушки,
24. 7 студентов выполняют контрольную работу в терминальном классе. Специальная программа случайным образом выдает каждому из них один из 10 разных вариантов. Какова вероятность, что все студенты получат разные варианты?
25. В коробке 5 красных, 7 зеленых и 8 желтых шаров. Наудачу вынимают 6 шаров. Найти вероятность того, что среди вынутых окажется по 2 шара каждого цвета.
26. Для регистрации в ОС RSX-IIМ требуется указать пароль. Пользователь "изобретает" пароль, набирая случайным образом последовательность из 6 символов латинского алфавита. Какова вероятность того, что пароль одинаково читается как слева направо, так и справа налево (например, "РАККАР")?
27. В пачке 2 книги из 20 имеют дефект переплета. Покупатель наудачу выбирает 5 книг. Найти вероятность того, что переплет одной из них имеет дефект.
28. На 6 вакантных мест в состав стройотряда имеется 20 кандидатов: 4 первокурсника, 6 второкурсников и 10 третьекурсников. Найти вероятность того, что при случайном выборе все первокурсники попадут в состав стройотряда.
29. 6 друзей купили по одному подарку. В новогоднюю ночь они сложили покупки в мешок и наудачу извлекли по очереди по одному подарку. Какова вероятность того, что в точности три человека извлекут свои подарки?
30. 5 студентов сдают экзамен. Каждому студенту экзаменатор случайным образом предлагает один из шести вопросов. Какова вероятность, что всем студентам достанутся разные вопросы?
ЗАДАЧА № 4
1. p и q - числа, случайно выбранные на отрезках [2,6] и [0, 4] соответственно. Найти вероятность, что корни уравнения х 2+ рx + q = 0 действительные.
2. Передатчик случайно включался в течение часа на 10 минут. Найти вероятность, что приемник, случайно прослушивавший эфир в течение 20 минут, заметил его работу.
3. Молодой человек договорился встретиться с девушкой между 9 и 10 часами и обещал ей ждать 30 минут. Девушка обещала ждать его 10 минут. Найти вероятность, что они встретятся.
4. На соседних сторонах прямоугольника с длинами сторон 10 и 20 м случайно выбраны точки. Найти вероятность, что расстояние между ними превосходит 4 м.
5. На противоположных сторонах квадрата со стороной I случайным образом выбраны точки, и квадрат разрезан по соединяющему эти точки отрезку. Найти вероятность, что площади получившихся трапеций отличаются не более чем в два раза.
6. На отрезке [0, 6] случайно берется число p , а затем на отрезке [0, р ]случайно выбирается число q. Найти вероятность, того что уравнение x 2 +р х+ q = 0 имеет действительные корни.
7. На сторонах АВ и АС равностороннего треугольника случайным образом выбраны точки М и N. Какова вероятность, что D AMN тупоугольный?
8. На отрезке [I,3] случайно выбраны два числа. Какова вероятность, что их сумма превосходит их произведение?
9. На сторонах АВ и АD квадрата АВСD выбраны точки М и N соответственно. Какова вероятность, что площадь треугольника АМN больше суммы площадей треугольников МВС и CDN?
10. На противоположных сторонах линейки шириной 3 см и длиной 20 см случайно сделаны насечки. Какова вероятность, что расстояние между ними меньше 5 см?
11. На первой ленте длиной 25 м покрасили случайно выбранный участок длиной 5 м. На второй ленте длиной 40 м закрасили случайно выбранный участок длиной 8 м. Ленты наложили друг на друга, совместив начала. Какова вероятность, что не менее 2 м крашенных частей будут перекрываться?
12. Число p случайно взято на отрезке [0, 2], а число q случайно взято на отрезке [p,2]. Какова вероятность, что их произведение pq не превосходит 1 ?
13. На стороне АВ и АС равностороннего треугольника АВС случайно взяты точки М и N. Какова вероятность, что площадь треугольника АМN больше площади треугольника NВС ?
14. Молодой человек договорился о встрече с девушкой между 11 и 12 часами. Девушка обещала ожидать молодого человека 10 минут после прихода, а молодой человек сказал, что он раньше 12 часов не уйдет. Какова вероятность, что они встретятся?
15. Числа р и q, случайно выбраны на отрезке [0, 2]. Какова вероятность, что уравнение x2 + p q x + 1 = 0 не имеет действительных корней?.
16. АВСD - прямоугольник со сторонами АВ = 2 и АD = I. На АВ и АD случайно выбраны точки М и N соответственно. Какова вероятность, что площадь треугольника АМN меньше площади треугольника МВС?
17. На сторонах АВ и АС квадрата АВСD случайно выбраны точки М и N . Какова вероятность, что треугольник АМN не имеет угла меньше 30° ?
18. Длины сторон прямоугольника равны 2 и 5. На каждой из длинных сторон случайно выбрано по точке. Какова вероятность, что тангенс угла между отрезком, соединяющим эти точки, и длинной стороной прямоугольника больше I и меньше 2 ?
19. На отрезке [0, I] случайно выбрано число p , а число q, случайно выбрано на отрезке [p , 4]. Какова вероятность, что модуль их разности больше их произведения?
20. На соседних сторонах квадрата случайно выбраны точки и отрезан треугольник с вершинами в этих точках. Какова вероятность, что площадь получившегося треугольника не превосходит четвертой части площади квадрата?
21. На отрезках [– 4, 4] и [-2, 2] случайно выбраны числа р и q, соответственно. Какова вероятность, что уравнение px2 + qx + p = 0 имеет действительные решения?
22. Длина магнитной ленты 100 м. На одной ее стороне сделана непрерывная запись длиной 30 м, на другой непрерывная запись длиной 20 м. Начала записей случайны. Из ленты вырезали участок длиной 10 м, начиная с ее середины. Найти вероятность того, что при этом повредили только одну из записей.
23. Случайно выбраны два неотрицательных числа p и q , в сумме не превосходящих 3. Какова вероятность, что уравнение x2- px + q = 0 не имеет действительных корней?
24. На одной стороне ленты длиной 15 м закрасили участок длиной 5 м, а на другой ее стороне закрасили участок длиной 4 м. Начала этих участков расположены случайно. Участок с 9-го по 10-й метр из ленты вырезали. Какова вероятность, что не задели оба покрашенных участка?
25. На отрезках [0, 2 ]и [0, 3] случайно выбрали числа р и q соответственно. Какова вероятность, что уравнение х2+(р+q)x+1 = 0 имеет действительные корни?
26. На катетах АВ и АС равнобедренного прямоугольного треугольника АВС случайно выбираются точки М и N и из них опускаются перпендикуляры MK и NL на гипотенузу ВС. Какова вероятность, что площадь пятиугольника КLNAМ больше половины площади треугольника АВС?
27. В треугольнике АВС С = 90°, А = 60°. На АВ и АС случайно взяты точки М и N соответственно. Какова вероятность, что треугольник AMN тупоугольный?
28. АВСD - прямоугольник со сторонами АВ = I и АD = 2. На АВ и АD случайно взяты точки М и N соответственно. Через М и N проведены прямые, параллельные, диагонали АС, которые отсекают от АВСD два треугольника. Какова вероятность, что сумма площадей этих треугольников больше половины площади всего прямоугольника?
29. В квадрате со стороной 8 нарисован отрезок длиной 2, проходящий параллельно стороне квадрата. Центры отрезка и квадрата совпадают. На квадрате случайным образом нарисована окружность единичного радиуса. Какова вероятность, что она пересечется с отрезком?
30. На прямоугольнике со сторонами 2 и  случайно выбирается точка. Какова вероятность, что обе длинные стороны прямоугольника видны из этой точки под острым углом?
случайно выбирается точка. Какова вероятность, что обе длинные стороны прямоугольника видны из этой точки под острым углом?
ЗАДАЧА № 5
1. Три стрелка выстрелили по мишени. При одном выстреле вероятность попадания для них 0,5; 0,7 и 0,9 соответственно. Найти вероятность, что мишень поражена не менее двух раз.
2. Для контроля за работой линии установлены три независимо работающих устройства, которые срабатывают при аварии с вероятностью 0,8; 0,9 и 0,95 соответственно. Найти вероятность, что при аварии сработает два устройства.
3. Из трех орудий производят залп по цели. Вероятность попадания при одном выстреле для первого орудия равна 0,9, а для второго и третьего соответственно 0,8 и 0,6. Найти вероятность того, что только одно орудие попадает в цель.
4. В урне 2 белых, 3 черных и 5 красных шаров. Наугад извлекают три шара. Найти вероятность, что они одного цвета.
5. Электрическая цепь составлена по схеме
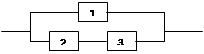 |
Элементы цепи выходят из строя независимо друг от друга с вероятностью 0,2; 0,1; 0,3 соответственно. Найти вероятность, что цепь будет пропускать ток.
6. Электрическая цепь составлена по схеме.
 |
Элементы цепи выходят из строя с вероятностью 0,1; 0,4; 0,5; 0,2 соответственно. Найти вероятность, что цепь будет пропускать ток.
7. Из 5 ключей к замку подходит один. Ими пытаются открыть дверь, откладывая не подошедшие ключи в сторону. Найти вероятность, что для открытия двери потребуется не более трех попыток.
8. Два стрелка стреляют по очереди, но не более трех раз каждый. Победителем считается тот, кто первым попадет в мишень. При одном выстреле они попадают в мишень с вероятностью 0,9 и 0,8. Найти вероятность, что победит более меткий стрелок, если он начал стрелять первым.
9. В урне 6 белых и 8 черных шаров. Взято подряд без возвращения два шара. Найти вероятность, что они одного цвета.
10. Рабочий обслуживает три станка, работающих независимо. Вероятность того, что в течение часа не потребует внимания рабочего: первый станок - 0,9; второй - 0,8; третий - 0,85. Найти вероятность того, что в течение часа два станка потребуют внимания рабочего.
11. В урне 2 белых и 3 черных шара. Два игрока вынимают из урны поочередно шары, не возвращая их обратно. Выигрывает тот, кто раньше извлечет белый шар. Найти вероятность того, что выиграет начинающий.
12. Рабочий обслуживает 4 независимо работающих станка, которые в течение часа требуют его внимания с вероятностью 0,1;0,1; 0,2 и 0,3 соответственно. Какова вероятность, что в течение часа не более одного станка потребуют его внимания?
13. Три стрелка выстрелили по мишени по одному разу. Вероятность попадания для них 0,9; 0,8 и 0,7 соответственно. Найти вероятность, что мишень поражена не более одного раза.
14. Стрелок имеет 6 патронов. При одном выстреле он попадает в мишень с вероятностью 0,7. Найти вероятность, что для поражения мишени ему потребуется не более половины патронов.
15. Прибор состоит из трех элементов. Отказы элементов за некоторое время Т независимы, а их вероятности равны соответственно 0,1; 0,2 и 0,25. Найти вероятность, что за время Т откажут два элемента.
16. В урне 5 белых и 4 черных шара. Из урны наугад один за другим без возвращения извлекаются шары. Найти вероятность того, что второй по порядку шар будет белым.
17. Электрическая цепь составлена по схеме.

Элементы цепи выходят из строя с вероятностью 0,1; 0,3; 0,1; 0,2 соответственно. Найти вероятность того, что цепь работает.
18. Из пяти деталей выбирают одну годную, проверяя их последовательно. Каждая из деталей имеет дефект с вероятностью 0,2. Найти вероятность того, что годная деталь нашлась раньше, чем проверили все детали.
19. Три стрелка производят по одному выстрелу по мишени. Вероятность попадания для первого стрелка 0,5; для второго - 0,8; для третьего - 0,3. Найти вероятность, что в мишени будет две пробоины.
20. Из колоды в 36 карт последовательно извлекают одну за другой три карты без возвращения. Найти вероятность того, что извлечено не более одного туза.
21. У мальчика имеется 4 монеты, на которые он хочет выпить лимонада. С вероятностью 0,1 автомат глотает монету, не наливая воды. Какова вероятность, что мальчик попьет, не истратив все монеты?
22. Ученику выдано три заготовки, из которых он должен изготовить деталь. Вероятность того, что он испортит заготовку при обработке, 0,7. Найти вероятность, что ему хватит заготовок для изготовления детали.
23. Студент подготовил к экзамену 30 из 40 вопросов. На экзамене ему выдается два обязательных вопроса. Если он их знает, ему выдается два дополнительных вопроса, из которых для сдачи экзамена необходимо ответить хоть на один. Найти вероятность, что студент сдаст экзамен.
24. Электрическая цепь составлена по схеме
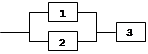 |
Элементы цепи выходят из строя за время Т с вероятностями 0,8; 0,6 и 0,9 соответственно. Найти вероятность разрыва всей цепи.
25. Прибор состоит из трех элементов, которые за время Т отказывают с вероятностью 0,1; 0,2 и 0,25 соответственно. Найти вероятность отказа двух элементов за время Т.
26. Вероятность попадания в мишень при одном выстреле равна 0,6. По мишени стреляют одиночными выстрелами до первого попадания. Найти вероятность того, что будет сделано не более трех выстрелов.
27. В урне 3 белых и I черный шар. Наугад один за другим без возвращения извлекают шары до тех пор, пока не появится черный. Найти вероятность того, что было проделано не более трех таких операций.
28. Среди 10 лампочек 3 имеют дефект. Их испытывают одну за другой, причем дефектная лампочка сразу при этом перегорает. Найти вероятность, что для выбора качественной пришлось испытать не более трех лампочек.
29. Прибор состоит из трех независимо работающих элементов, которые за время Т отказывают с вероятностью 0,1; 0,2 и 0,3 соответственно. Найти вероятность отказа двух элементов за время Т.
30. Из колоды в 52 карты последовательно извлекают одну за другой три карты без возвращения в колоду. Найти вероятность того, что извлечена только одна десятка.
ЗАДАЧА № 6
1. В семи урнах содержится по 2 белых и 2 черных шара, а в трех урнах по 7 белых и 3 черных шара. Какова вероятность, что из урны, взятой наудачу, будет извлечен белый шар? Найти вероятность, что шар извлечен из урны с 7 белыми и 3 черными шарами, если он оказался белым,
2. Станок 30 % времени обрабатывает деталь А и 70 % - деталь В. При обработке детали А он простаивает 10 % времени, а детали В - 15 %. Какова вероятность застать станок простаивающим? Найти вероятность, что станок, который застали простаивающим, находится в режиме обработки детали В.
3. Сборщик получает 45 % деталей завода № I, 30 % - завода № 2, остальные - с завода № 3. Вероятность того, что деталь первого завода отличного качества 0,7; для деталей второго и третьего заводов эти вероятности равны соответственно 0,8 и 0,9. Найти вероятность, что наудачу взятая сборщиком деталь окажется отличного качества. Какова вероятность, что взятая наудачу деталь, оказавшаяся отличного качества, изготовлена заводом № I?
4. Деталь проходит одну из трех операций обработки с вероятностью 0,25; 0,35; 0,40 соответственно. Вероятность получения брака на первой операции равна 0,02, на второй - 0,04, а на третьей - 0,05. Найти вероятность получения брака после обработки. Какова вероятность, что деталь прошла третью операцию обработки, если подучен брак?
5. По цели производится три выстрела с вероятностью попадания 0,2 при каждом. Вероятность уничтожения цели при одном попадании равна 0,3; при двух попаданиях - 0,6; при трех - 0,9. Найти вероятность уничтожения цели. Какова вероятность, что было одно попадание, если цель уничтожена?
6. В первой урне 4 белых и 6 черных шаров, во второй 5 белых и 4 черных. Из первой урны во вторую перекладывают, не глядя, один шар, после чего из второй урны извлекается один шар. Найти вероятность, что этот шар белый. Какова вероятность, что из первой во вторую урну был переложен черный шар, если извлеченный из второй урны шар оказался белым?
7. В цехе имеются три станка. Вероятность изготовления стандартной детали на первом станке составляет 0,78; на втором-0,92; на третьем - 0,86. Ввиду различного местоположения рабочий выбирает первый станок с вероятностью 0,5; второй - 0,2; третий-0,3. Найти вероятность, что изготовленная им на выбранном станке деталь окажется нестандартной. Какова вероятность того, что деталь изготавливалась на третьем станке, если она оказалась нестандартной?
8. По команде "огонь" одно из трех орудий стреляет по мишени. Вероятность попадания для орудий равна соответственно 0,8; 0,8; 0,6. Команда "огонь" подается в 2 раза чаще первому орудию, чем второму и третьему по отдельности. Найти вероятность, что мишень окажется пораженной. Какова вероятность того, что мишень была поражена выстрелом из 3-го орудия?
9. В первой урне 3 белых и 2 черных шара; во второй 3 белых и 5 черных. Из первой во вторую перекладывают, не глядя, два шара, после чего из второй урны извлекается шар. Найти вероятность того, что этот шар окажется белым. Какова вероятность того, что из первой во вторую урну были переложены белый и черный шары, если из второй урны извлечен белый шар?
10. На сборку поступили транзисторы с двух заводов-изготовителей, причем первый завод поставил 30 %, остальные - второй. Вероятность отказа для транзистора первого завода 0,1 , а второго - 0,15. В блок поставлено два наудачу взятых транзистора. Найти вероятность, что блок неисправен. Какова вероятность, что оба транзистора изготовлены вторым заводом, если блок неисправен? Блок не работает, если дефект имеет хоть один транзистор.
11. Пятнадцать экзаменационных билетов содержат по два вопроса, которые не повторяются. Экзаменующийся может ответить только на 25 вопросов. Определить вероятность того, что экзамен будет сдан, если для этого достаточно ответить на два вопроса из одного билета или на один вопрос из первого билета и на указанный дополнительный вопрос из другого билета. Какова вероятность того, что студент сдал экзамен, ответив на вопросы из одного билета?
12. На общий конвейер поступают узлы, изготовленные двумя рабочими. Производительность второго рабочего вдвое больше, чем первого. Вероятность допустить брак для первого рабочего 0,075 , а для второго 0,09. Найти вероятность, что поступивший на общий конвейер узел будет иметь брак. Какова вероятность, что узел, оказавшийся бракованным, изготовлен вторым рабочим?
13. Покупатель приобрел электролампочку. Известно, что в момент покупки партия лампочек содержала 60% продукции местного предприятия и 40% -иногороднего. 500 часов работают безотказно каждые 90 из 100 лампочек местного завода и 80 из 100 иногороднего. Найти вероятность, что купленная лампочка проработает 500 часов. Какова вероятность того, что лампочка, проработавшая 500 часов безотказно, местного производства?
14. Узлы поступают на общий конвейер с двух участков. Вероятность брака узла с первого участка 0,05, со второго - 0,10. Второй участок имеет производительность в 1,5 раза больше, чем первый. Найти вероятность того, что взятый с конвейера узел окажется годным. Какова вероятность того, что годный узел изготовлен на первом участке?
15. Из урны, содержащей 3 белых и 2 черных шара, переложено два шара в урну, содержащую 4 белых и 4 черных шара. Вычислить вероятность вынуть белый шар из второй урны. Какова вероятность, что из первой во вторую урну было переложено 2 черных шара, если из второй урны извлеченный наудачу шар оказался белым?
16. Первое орудие четырехорудийной батареи пристреляно так, что вероятность попадания равна 0,4. Остальные три орудия попадают с вероятностью 0,2. Для поражения цели достаточно одного попадания. Два орудия произвели по выстрелу. Найти вероятность поражения цели. Какова вероятность того, что первое орудие стреляло, если цель оказалась пораженной?
17. Для сигнализации о неполадке в работе автоматической линии используется один индикатор, принадлежащий с вероятностями 0,2; 0,3 и 0,5 к одному из трех типов, для которых вероятности срабатывания при нарушении нормальной работы линии равны соответственно 1; 0,75 и 0,40. Найти вероятность, что индикатор срабатывает при неполадке в работе линии. Какова вероятность, что дня контроля используется индикатор 1-го типа, если он подал сигнал о произошедшей в работе линии неполадке?
18. Транзистор принадлежит к одной из трех партий с вероятностями 0,25; 0,5 и 0,25. Вероятность того, что транзистор проработает заданное число часов, для этих партий равна соответственно 0,8; 0,8 и 0,6. Определить вероятность, что транзистор проработает заданное число часов. Какова вероятность того, что проработавший заданное число часов транзистор принадлежит второй партии?
19. На сборку поступают детали с двух автоматов. Первый автомат дает 80 %, остальные - второй. Первый автомат дает 1% брака, второй - 4%. Найти вероятность, что две проверенные детали окажутся бракованными. Определить вероятность того, что обе проверенные детали, оказавшиеся бракованными, изготовлены первым автоматом.
20. Из 20 стрелков 5 попадают в мишень с вероятностью 0,8; 8 - с вероятностью 0,7 ; 4 - с вероятностью 0,6 и 3 - с вероятностью 0,5. Наудачу выбранный стрелок произвел выстрел. Какова вероятность того, что он промахнется? Найти вероятность того, что выбран стрелок из группы пяти метких, если он промахнулся.
21. Из 10 студентов, пришедших на экзамен, 3 подготовлены отлично, 4 - хорошо, 2 - посредственно и I плохо. На экзамен вынесено 20 вопросов. Отлично подготовленный студент знает все вопросы, хорошо подготовленный знает 16, посредственно - 10, плохо - 5. Найти вероятность, что вызванный наугад студент ответит на три произвольно заданных различных вопроса. Какова вероятность того, что студент, ответивший на три вопроса, подготовлен плохо?
22. Три монтажника ведут сборку однотипных приборов, причем производительности их труда относятся как 2:3:5. Вероятности сборки прибора отличного качества у них равны соответственно 0,8; 0,6 и 0,6. Найти вероятность, что взятый наудачу изготовленный ими прибор окажется отличного качества. Какова вероятность того, что прибор изготовлен первым рабочим, если он оказался отличного качества?
23. В первой урне 3 белых и 5 черных шаров, во второй 5 белых и 4 черных, а в третьей урне 2 белых и 3 черных шара. Из наугад выбранной урны извлекают один шар. Найти вероятность, что этот шар белый. Какова вероятность, что шар извлекался из первой урны, если он оказался белым?
24. На сборку поступают детали с трех автоматов. Первый автомат делает 20% деталей, второй - 30 %, остальные - третий. Первый автомат дает 0,2% брака, второй - 0,3%, третий. - 0,1%. Найти вероятность поступления на сборку бракованной детали. Определить вероятность того, что бракованная деталь поступила на сборку с первого автомата,
25. В первой урне 3 белых и 4 черных шара, во второй - 5 белых и 2 черных шара. Из выбранной наугад урны достали 2 шара. Найти вероятность, что они оба белые. Какова вероятность, что шары извлекли из второй урны, если они оба белые?
26. Вероятность выхода. Из строя первого, второго и третьего элементов прибора равна соответственно 0,1; 0,2 и 0,3. Вероятность отказа прибора при выходе из строя одного элемента равна 0,2; двух элементов - 0,5; трех - 1. Определить вероятность отказа прибора. Найти вероятность того, что вышел из строя только один элемент, если прибор отказал.
27. Некоторое изделие выпускается двумя заводами. При этом объем продукции второго завода в 1,5 раза превосходит объем продукции первого. Доля брака у первого завода 18%, а у второго -8 %. Изделия, выпущенные заводами за одинаковый промежуток времени, перемешали и пустили в продажу. Найти вероятность покупки бракованного изделия. Какова вероятность, что купленное бракованное изделие изготовлено на первом заводе?
28. На рубеж случайно вызывается один из трех стрелков. Вероятность вызова первого стрелка равна 0,3; второго - 0,5; третьего - 0,2. Вероятности попадания для них 0,8; 0,9 и 0,6 соответственно. Найти вероятность, что цель будет поражена. Какова вероятность того, что стрелял второй стрелок, если цель поражена?
29. На сборку поступают детали с двух заводов-изготовителей, причем они поставляют их в равном количестве. У первого завода брак составляет 4%, у второго - 3%. Наугад взяли две детали. Найти вероятность, что они обе доброкачественные. Какова вероятность, что эти детали изготовлены первым заводом, если они обе доброкачественные?
30. Станок обрабатывает три вида деталей, причем затраты времени распределяются между ними в отношении 1:5:4. При обработке первой детали станок работает с максимальной нагрузкой в течение 70 % времени, при обработке второй детали в течение 50%, а третьей - 20 % времени. Найти вероятность того, что в случайно выбранный момент времени станок будет работать с максимальной нагрузкой. Какова вероятность того, что работающий с максимальной нагрузкой станок обрабатывает деталь третьего вида?
ЗАДАЧА № 7
Найти закон распределения, математическое ожидание и дисперсию случайной величины Х. Построить график функции распределения и найти вероятность события Х £ К.
1. Ведется стрельба до первого попадания, но не свыше 5 выстрелов. Вероятность попадания при каждом выстреле равна 0,7. X - число произведенных выстрелов. К = 3.
2. Партия из 20 деталей содержит 4 бракованных. Произвольным образом выбрали 5 деталей. Х - число доброкачественных деталей среди отобранных. К = 2.
3. У стрелка, вероятность попадания которого в мишень равна 0,65 при каждом выстреле, имеется 5 патронов. Стрельба прекращается при первом же попадании. Х - число оставшихся патронов. К = 3.
4. Прибор содержит три элемента, вероятности отказов которых за определенное время независимы и равны соответственно 0,15; 0,2 и 0,25. X - число отказавших элементов. К = 2.
5. В урне 4 белых и 3 черных шара. Наудачу один за другим извлекаем шары из урны до появления белого шара. Х - число извлеченных черных шаров. К = 3.
6. На пути автомашины 4 независимых друг от друга светофора, каждый из которых с вероятностью 0,4 запрещает движение. X - число пройденных до первой остановки светофоров. К = 2.
7. По мишени одновременно стреляют 3 стрелка, вероятности попаданий которых равны соответственно 0,65; 0,7 и 0,8. X - число попаданий. К = I.
8. В темной комнате 7 красных кубиков и 8 синих, не отличных друг от друга на ощупь. Мальчик вынес 3 кубика. Х - число красных кубиков среди вынесенных. К=2.
9. Производится набрасывание колец на колышек до первого успеха, при этом число всех колец, имеющихся в распоряжении, равно 5. X - число использованных колец, вероятность набрасывания равна 0,25. К = 2.
10. Производится выстрел из трех орудий одновременно по цели с вероятностями попадания 0,5; 0,6 и 0,7 для каждого орудия. X - число попаданий. К = I.
11. В урне 4 белых и 5 черных шаров. Наудачу один за другим из урны извлекаются шары до появления первого черного. X - число оставшихся в урне белых шаров. К = 2.
12. Некто забыл последнюю цифру шифра кодового замка. Зная, что это одна из цифр 5,6,7,8,9, он случайным образом их перебирает. X- число попыток, К = 2.
13. Вероятность попадания в цель из орудия при первом выстреле равна 0,3; при втором - 0,4; при третьем - 0,5; при четвертом - 0,9. Стрельба ведется до первого попадания, но не свыше 4 выстрелов. X- число произведенных выстрелов. К=3.
14. В партии из 10 деталей содержится 7 деталей первого сорта. Случайным образом одну за другой без возвращений извлекаем детали до появления детали первого сорта. X - число попыток. К = 2.
15. По мишени ведется стрельба до первого попадания, но не более 4 раз. Вероятность попадания при каждом выстреле 0,9. X - число выстрелов. К = 2.
16. Вероятность попадания в цель из орудия при первом выстреле равна 0,1; при втором 0,3; при третьем 0,5; при четвертом 0,8. Производится 4 выстрела. X - число попаданий в цель. К = I.
17. Одновременно бросаются 4 монеты. Х - число выпавших "орлов". К = 3.
18. В партии из 15 деталей 10 деталей первого сорта, остальные второго. Отобраны случайным образом 4 детали. X - число деталей второго сорта среди отобранных. К = 3.
19. Трасса движения слаломиста состоит из четырех участков, каждый из которых он проходит с вероятностью 0,8. В случае непрохождения одного из них спортсмен снимается с трассы. X - число пройденных участков. К = 2.
20. Бросаются 5 монет одновременно. X - число выпавших "орлов". К = 3.
21. Баскетболист бросает мяч в корзину до первого попадания, но делает не более 5 раз. Вероятность попадания при каждом броске 0,4. X - число сделанных бросков. К = 4.
22. В группе из 6 изделий одно бракованное. Изделия выбирают одно за другим наугад до появления бракованного. X - число извлеченных доброкачественных изделий. К = 2.
23. В урне 5 черных, 3 белых и 2 красных шара. Наугад вынимаем 3 шара. Х - число различных цветов среди вынутых шаров. К= 2.
24. Производятся последовательные независимые испытания пяти приборов на надежность. Следующий проверяется только в том случае, если предыдущий прибор оказался ненадежным. Каждый прибор надежен с вероятностью 0,7. X - число проверенных приборов. К = 2.
25. Среди 10 деталей имеется 4 бракованных. Извлекаем случайным образом без возвращений детали до тех пор, пока не вынем доброкачественную. Х - число вынутых деталей. К = 3.
26. В приборе имеется три элемента, вероятности отказа которых за определенное время равны соответственно 0,2; 0,3; 0,4. Отказы элементов независимы. Х - число отказавших элементов. К = 2.
27. Из партии в 10 деталей, среди которых 4 бракованных, произвольным образом выбраны 3 детали. X - число бракованных деталей среди отобранных. К = I.
28. По мишени одновременно стреляют 4 стрелка с вероятностью попадания 0,6 для каждого. X - число попаданий. К = 2.
29. В ящике 4 пары одинаковых ботинок. Вынимаем ботинки, не глядя, один за другим до тех пор, пока не составится пара. Х - число вынутых ботинок. К = 3.
30. Известно, что при бросании двух игральных костей сумма выпавших очков нечетна. Х - сумма очков. К= 5.
ЗАДАЧА №8
В случаях а, б и в рассматривается серия из n независимых испытаний с двумя исходами в каждом - "успех" или "неуспех". Вероятность "успеха" равна p, "неуспеха" q= 1-p в каждом испытании. X - число "успехов" в n испытаниях. Требуется:
1) для случая a (малого n ) построить ряд распределения, функцию распределения X, найти МХ, DХ и Р(Х£2) ;
2) для случая б (большого N и малого p ) найти Р(Х £2) приближенно с помощью распределения Пуассона. Оценить точность приближения;
3) для случая в (большого N) найти вероятность P( k1£ X £k2 ) приближенно с помощью теоремы Муавра-Лапласа.
| Вариант | Случай а n p | Случай б N p | Случай в N p k1 k2 | |||||
| 0,2 | 0,002 | 0,2 | ||||||
| 0,4 | 0,004 | 0,4 | ||||||
| 0,9 | 0,002 | 0,25 | ||||||
| 0,5 | 0,01 | 0,1 | ||||||
| 0,15 | 0,015 | 0,2 | ||||||
| 1/3 | 0,02 | 0,4 | ||||||
| 0,1 | 0,0025 | 0,25 | ||||||
| 0,4 | 0,004 | 0,9 | ||||||
| 1/3 | 0,0025 | 0,8 | ||||||
| 0,7 | 0,007 | 0,6 | ||||||
| 0,8 | 0,002 | 0,75 | ||||||
| 0,1 | 0,001 | 0,1 | ||||||
| 0,3 | 0,003 | 0,8 | ||||||
| 0,08 | 0,004 | 0,6 | ||||||
| 0,3 | 0,01 | 0,75 | ||||||
| 0,1 | 0,02 | 0,1 | ||||||
| 0,6 | 0,01 | 0,9 | ||||||
| 0,5 | 0,0085 | 0,2 | ||||||
| 0,25 | 0,005 | 0,4 | ||||||
| 0,75 | 0,015 | 0,1 | ||||||
| 2/3 | 0,02 | 0,8 | ||||||
| 0,7 | 0,01 | 0,6 | ||||||
| 0,3 | 0,001 | 0,2 | ||||||
| 0,5 | 0,01 | 0,4 | ||||||
| 0,4 | 0,003 | 0,25 | ||||||
| 0,15 | 0,02 | 0,1 | ||||||
| 0,2 | 0,01 | 0,8 | ||||||
| 0,8 | 0,008 | 0,6 | ||||||
| 0,6 | 0,004 | 0,75 | ||||||
| 0,25 | 0,008 | 0,9 |
ЗАДАЧА № 9 .
Плотность распределения f(х) случайной величины X на (а, в ) задана в условии, а при xÏ (а, в ) ; f (x)= 0. Требуется:
1) найти параметр А ;
2) построить графики плотности и функции распределения;
3) найти математическое ожидание МХ, дисперсию DХ и среднее квадратическое отклонение d ;
4) вычислить вероятность Р того, что отклонение случайной величины от математического ожидания не более заданного e
| Вариант | f (x) | (а,в) | e |
| I | Ах + 1/3 | (0,1) | 1/2 |
| 2х + А | (0,1) | 1/3 | |
| Ах2 | (0,1) | 1/2 | |
| А(2х + 1) | (0,2) | 1/3 | |
| А(х + 2) | (0,2) | ||
| A (1-x2) | (0,1) | 1/8 | |
| 2-Ax | (0,1) | 1/3 | |
| A (2x2+1) | (0,1) | 1/10 | |
| A (4+3x) | (0,1) | ||
| A(x2+1) | (0,2) | ||
| A(4x2+1) | (0,1) | 1/7 | |
| A(2+3x) | (0,1) | 1/2 | |
| Ax2+3/4 | (0,1) | 1/2 | |
| A(1+6x) | (0,1) | 1/8 | |
| A(1+3x2) | (0,1) | 1/4 | |
| Ax2+ 1/4 | (0,2) | 1/2 | |
| Ax2+ 1/3 | (0,1) | 1/3 | |
| A(3x2+2) | (0,1) | 1/4 | |
| (3/8)x2+A | (0,2) | ||
| 3x2+A | (0,1) | 1/2 | |
| A(6x2+1) | (0,1) | 1/3 | |
| Ax2+1/2 | (0,1) | 1/8 | |
| Ax+3/7 | (0,1) | 1/14 | |
| Ax2+ 3/5 | (0,1) | 1/5 | |
| Ax2+ 3/2 | (0,1) | 1/8 | |
| 3/2+Ax | (0,3) | 1/2 | |
| (1/2)x+A | (0,2) | 1/3 | |
| Ae -|x-1| | (-¥;¥) | ||
| 4e-4x+A | (0, ¥) | 1/2 | |
| 1-Ax | (0,1) | 1/4 |
ЗАДАЧА № 10
Случайное отклонение размера детали от номинала распределено по нормальному закону с математическим ожиданием а и средним квадратическим отклонением d. Годными считаются детали, для которых отклонение от номинала лежит в интервале [a-e ;a+e ]
Требуется:
1) записать формулу плотности распределения и построить график плотности;
2) вычислить таблицу функции распределения отклонения для значений x = a + kb , k = 0, ± 1, ± 2, ± 3 и построить график;
3) найти вероятность того, что при выборе наудачу n деталей отклонение каждой из них попадает в интервал [a;b];
4) определить, какое наименьшее число деталей необходимо изготовить, чтобы среди них с вероятностью не меньшей, чем Р , хотя бы одна деталь была годной.
Замечание. В пп. 3, 4 пользоваться линейной интерполяцией при отсутствии нужного значения в таблице.
| Вариант | a | d | a | b | n | P | e |
| I | -1,29 | 2,25 | 0,95 | 2,564 | |||
| I | 1,718 | 3,524 | 0,99 | 1,645 | |||
| -I | -6,185 | -0,375 | 0,99 | 5,185 | |||
| -2,526 | 0,771 | 0,992 | 3,846 | ||||
| -2 | 0,2 | -2,135 | -1,923 | 0,95 | 0,2074 | ||
| I | 0,5 | 0,738 | 1,421 | 0,95 | 0,641 | ||
| -I | -1,77 | 0,35 | 0,999 | 3,29 | |||
| I | -0,257 | 1,282 | 0,91 | 1,037 | |||
| I | 0,625 | 4,111 | 0,99 | 4,935 | |||
| -2 | I | -2 | -0,718 | 0,97 | 1,645 | ||
| -2 | -3,684 | 2,514 | 0,992 | 2,564 | |||
| -I | -1,375 | 2,111 | 0,99 | 4,935 | |||
| -6,58 | 0,5 | 0,95 | 5,128 | ||||
| -I | 0,4 | -1,154 | 1,7 | 0,999 | 0,658 | ||
| 0,926 | 3,25 | 0,99 | 2,074 | ||||
| I | -0,028 | 6,028 | 0,91 | 4,148 | |||
| -3,1 | 9,62 | 0,95 | 12,444 | ||||
| -I | I | -2,282 | -0,476 | 0,99 | 1,645 | ||
| I | I | 3,564 | 0,97 | 3,29 | |||
| 1,5 | -0,786 | 1,263 | 0,95 | 1,923 | |||
| -I | I | -1,842 | -0,743 | 0,992 | 1,282 | ||
| I | -3,945 | 1,375 | 0,95 | 3,846 | |||
| -3 | I | -4,037 | -2,875 | 0,99 | 1,037 | ||
| 0,05 | 1,9738 | 2,0241 | 0,95 | 0,0641 | |||
| -10 | -10 | -4,872 | 0,97 | 6,58 | |||
| -4,05 | 2,31 | 0,95 | 6,222 | ||||
| I | -5,41 | 3,62 | 0,99 | 8,225 | |||
| I | 9,296 | 0,99 | 13,16 | ||||
| -I | -6,14 | 24,64 | 0,91 | 20,74 | |||
| -1,85 | 8,75 | 0,999 | 16,45 |
ЗАДАЧА № 11
Случайная величина X имеет плотность распределения f(x), случайная величина Y= j(X). Найти закон распределения случайной величины Y , ее математическое ожидание и дисперсию.
В вариантах 1...15 случайная величина X равномерно распределена на промежутке [а, b] .
В вариантах 16...25 случайная величина X распределена по закону:

В вариантах 26..30 случайная величина Х распределена по нормальному закону с параметрами а и d.
1.a= -p/ 2, b = p/2, j (x)= sin x
2. a= -p/ 2, b = p/2, j (x)= cos x
3. a=0, b=p, j (x)= sin x
4. a=0, b=p, j (x)= cos x
5. a= -p/ 2, b = p/2, j(x)= |sin x|
6. a= 0, b = p, j (x)= |cos x|
7. a=0, b=e, j (x)= ln x
8. a=1, b=3, j (x)= ex
9. a =0, b=e, j (x)= |ln x|
10. a =-2, b=2, j (x)= х2
11. a =-1, b=1, j (x)= e-x
12. a =-3, b=3, j (x)= x4
13. a =0, b=1, j (x)= arctg x
14. a =2, b=4, j (x)= 1/x3
15. a =-1, b=1, j (x)= |x|
16. aa=0, b = p/2, j (x)= sin x
17. aa=0, b=p, j (x)= cos x
18. a =0, b = p/2, j (x)= cos x
19. a =0, b=p, j (x)= sin x
20. a =0, b=2, j (x)= x3
21. a = a 0, b = p, j (x)= |cos x|
22. a =1, b=e, j (x)= ln x
23. a =e-1, b=e, j (x)= |ln x|
24. a=1, b=2, j (x)= x4
25. a=1, b=3, j (x)= x2
26. a =0, d =1, j (x)= 
27. a =0, d =3, j (x)=