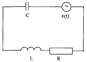
Введение

Колебательная система, выведенная из состояния равновесия, начинает колебаться с собственной частотой. Из-за неизбежных потерь энергии колебания являются затухающими, и со временем система возвращается в состояние равновесия.

Чтобы колебания не затухали, колебательную систему нужно пополнять энергией. Тогда под действием внешней, периодически изменяющейся силы, под действием которой система совершает вынужденные колебания.

В случае электрических колебаний это можно осуществить, если включить последовательно с элементами контура переменную ЭДС или, разорвав контур, подать на образовавшиеся контакты переменное напряжение (рис. 1).

 

Используя закон Ома для замкнутой цепи, получим для данного контура выражение:

, (1)

где 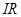– падение напряжения на активном сопротивлении ; – падение напряжения на емкости; – ЭДС самоиндукции; ( ) – внешний источник ЭДС.

Учитывая, что ЭДС изменяется по гармоническому закону, получим:

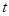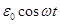( )= , а .

Преобразуем уравнение (1) к виду:

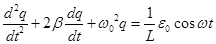, (2)

где 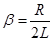– коэффициент затухания свободных колебаний в контуре, – частота собственных колебаний контура.

Спустя некоторое время после подключения источника ЭДС, в контуре устанавливаются вынужденные колебания с постоянной амплитудой. Установившиеся вынужденные колебания заряда и силы тока в контуре описываются уравнениями:

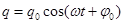, (3)

. (4)

Амплитуда силы тока и начальная фаза находятся по формулам:

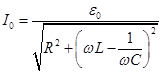, (5)

. (6)

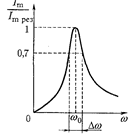
Графики зависимости при различных значениях сопротивления , называемые резонансными кривыми колебательного

контура, представлены на рисунке 2.

 

 

Из формулы (5) следует, что амплитуда силы тока в контуре 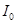зависит от частоты питающего напряжения и она будет максимальна при частоте, отвечающей условию , называемой резонансной частотой . Выражая отсюда , получаем:

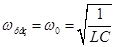. (7)

Таким образом, частота внешней вынуждающей ЭДС станет равной частоте собственных колебаний контура.

Резонансная циклическая частота не зависит от сопротивления . Амплитуда силы тока при резонансе равна . Амплитуда падения напряжения на конденсаторе равна амплитуде падения напряжения на индуктивности (ЭДС самоиндукции):

,

.

При резонансный пик (амплитуда силы тока ) уходит в бесконечность, при этом энергия постоянно вводится в систему и не рассеивается. В реальных системах сопротивление никогда не равно нулю, поэтому резонансный пик имеет конечную высоту.

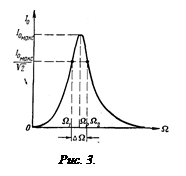«Остроту» резонансной кривой можно охарактеризовать с помощью относительной ширины этой кривой. Она определяется как 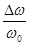, где - разность значений и 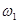циклических частот, соответствующих (рис. 3).

 

Полагая в формуле (5) , получаем:

или

.

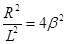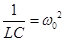Заменив и , получим следующее уравнение, которому удовлетворяют искомые значения 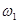и циклической частоты:

.

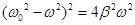Это биквадратное уравнение эквивалентно следующим двум квадратным уравнениям: 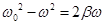и .

Решая их совместно и отбрасывая отрицательные корни, так как они не соответствуют физическому смыслу , находим, что:

,

,

.

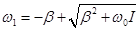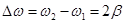Относительная ширина резонансной кривой колебательного контура равна отношению активного сопротивления контура к его волновому сопротивлению:

. (8)

Колебательную систему принято характеризовать добротностью – безразмерной величиной, равной произведению 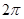на отношение энергии колебаний системы в произвольный момент времени к убыли этой энергии за промежуток времени от 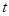до 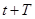, т.е. за один условный период затухающих колебаний:

.

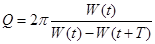Можно показать, что при малых значениях коэффициента затухания ( <<1) добротность колебательной системы равна:

. (9)

Из (9) видно, что относительная ширина резонансной кривой колебательного контура есть величина, обратная добротности контура :

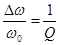. (10)

В радиотехнике качество резонансного контура считается тем выше, чем больше его добротность (рис. 4).

Колебательный контур широко применяется в радиотехнике для приема сигналов радиостанций, работающих на фиксированных частотах, в измерительной технике для создания селективных вольтметров, реагирующих на выбранную частоту и нечувствительных к сигналам (помехам) других частот.