A3 (базовый уровень, время – 3 мин)

Тема: Умение анализировать формальные описания реальных объектов и процессов.

Что нужно знать:

· если объекты некоторой системы отобразить вершинами, а связи между ними – линиями (ребрами), то получим граф;

· взвешенный граф – это граф, с каждым ребром которого связано некоторое число (вес), оно может обозначать, например, расстояние между городами или стоимость перевозки;

· с помощью взвешенного графа можно, например, изобразить дороги между населенными пунктами, где вес ребер – протяженность дорог в километрах (см. рисунок);

· по взвешенному графу может быть построена таблица (весовая матрица).

	A	B	C	D	Е
A
B
C
D
Е

 

 

Задача 1:

Между населёнными пунктами A, B, C, D, E, F построены дороги,
протяжённость которых (в километрах) приведена в таблице.

	A	B	C	D	Е	F
A
B
C
D
Е
F

 

 

Определите длину кратчайшего пути между пунктами A и F. Передвигаться
можно только по дорогам, указанным в таблице.

1) 9 2) 11 3) 13 4) 15

Решение:

1) Для удобства отобразим табличные данные в виде графа. Для этого на листе расставляем точки — населенные пункты. В соответствии с таблицей соединяем их и подписываем расстояния.

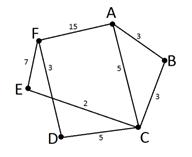
2) Переберем все возможные пути из A в F:

A-B-C-E-F = 3+3+2+7 = 15

A-B-C-D-F = 3+3+5+3 = 14

A-C-E-F = 5+2+7 = 14

A-C-D-F = 5+5+3 = 13

A-F = 15

Как видно, кратчайший вариант A-C-D-F = 13 км.

ВНИМАНИЕ:Чтобы не запутаться, рекомендуется перебирать пункты в алфавитном порядке.