Постоянный ток

Примеры решения задач

27. Пространство между пластинами плоского конденсатора заполнено многослойным диэлектриком, обладающим слабой электропроводностью. Диэлектрическая проницаемость диэлектрика монотонно уменьшается от пластины 1 от значения до значения у пластины 2. Удельная электропроводность монотонно уменьшается от пластины 1 от значения Ом.^-1 м^-1 до значения Ом.^-1 м^-1 у пластины 2. Конденсатор включен в цепь с постоянной ЭДС, и в нем устанавливается постоянный электрический ток силой А, текущий через диэлектрик от стороны 1 конденсатора к стороне 2. Найти величину свободного заряда , возникшего в диэлектрике при протекании тока.

Дано: Ом.-1м-1 Ом.-1м-1 А	Решение Среда между пластинами конденсатора обладает как электропроводящими, так и диэлектрическими свойствами. Поэтому в решении используется закон Ома в дифференциальной форме: , (1) где – плотность тока; - напряженность электрического поля, и теорема Гаусса для диэлектрика. Направление линий тока вектора и направления векторов
– ?

электрического смещения и у пластины 1 и пластины 2 соответственно показаны на рисунке.

Ток через среду постоянный, линии тока перпендикулярны к пластинам конденсатора, следовательно, для величин силы тока у пластины 1 и пластины 2 можно записать

где - площадь пластины конденсатора. Это же соотношение с учетом закона Ома (1) принимает форму

(2)

Для использования теоремы Гаусса проведем гауссову поверхность в виде прямоугольного параллелепипеда (пунктирная линия на рисунке), так, чтобы внутри находился диэлектрик. По теореме Гаусса для диэлектрика, учитывая направление векторов , имеем:

(3)

Связь между вектором электрического смещения 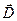и напряженностью электрического поля, как известно имеет вид:

(4)

Из соотношений (2) – (4) для величины заряда следует

Кл.

Ответ: нКл.

 

28. В схеме, изображенной на рисунке В, В, В, Ом, Ом, Ом. Внутреннее сопротивление источников тока пренебрежимо мало. Определить силы токов , , , текущих через сопротивления.

 

Дано: В В В Ом Ом Ом	Решение
– ? – ? – ?

Представленная в задаче схема постоянного тока, может быть рассчитана на основе законов Кирхгофа. Для применения законов Кирхгофа выделим два замкнутых контура АBCDА и AFЕBА. Зададим направление обхода этих замкнутых контуров по часовой стрелке, как показано на рисунке. Также будем рассматривать узел схемы А, в котором сходятся (или вытекают) токи , , .

По первому закону Кирхгофа для токов узла А следует уравнение:

(1)

В данном выражении учитывалось правило знаков: ток втекает в узел – положителен, ток вытекает из узла – отрицателен.

По второму закону Кирхгофа для контуров ABCDА и AFЕBА имеем соответственно:

(2)

. (3)

В выражениях (2) и (3) учитывалось правило знаков, определяемое выбранным направлением обхода контура. ЭДС положительна, если направление обхода контура совпадает с направлением ЭДС.

Подставляя известные численные значения сопротивлений участков цепи и ЭДС источников тока в уравнения (1) – (3), получим

(4)

Таким образом, получается система трех линейных уравнений с тремя искомыми неизвестными , , . Решение такой системы дается формулами Крамера:

, , , (5)

где – определитель системы (4); – определитель при первом неизвестном ; – определитель при втором неизвестном ; – определитель при третьем неизвестном .

По значениям коэффициентов системы уравнений (4) следует:

(6), (7)

(8), (9)

Из выражений (5) – (9) для величин сил токов получается

А, А, А.

Ответ: А; А; А.

29. Сила тока в проводнике убывает со временем по закону ( А, с^-1). Определить заряд, прошедший через поперечное сечение проводника за время с.

Дано: А с-1 с	Решение Величина силы тока связана с зарядом q, проходящим через поперечное сечение проводника, соотношением . (1) Следовательно, за бесконечно малый промежуток времени через поперечное сечение проводника пройдет заряд
– ?

(2)

Величина заряда q, прошедшего через поперечное сечение проводника за промежуток времени , может быть найдена интегрированием выражения (2):

Кл.

Ответ: Кл.

 

30. В медном проводнике объемом см³ при прохождении по нему постоянного тока за время ,0 мин выделилось количество теплоты Дж. Найти напряжённость электрического поля в проводнике, плотность тока , скорость упорядоченного движения электронов . Считать, что на каждый атом меди приходится один свободный электрон.

Проводимость, плотность и молярная масса меди соответственно ,

Дано: 6,0 см3 = ,0×10-6 м3 мин = 60 с Дж Ом-1×м-1 Кг/м3 г/моль = 63,5×10-3 кг/моль	Решение а) для решения используем закон Ома в дифференциальной форме , (1) закон Джоуля – Ленца в дифференциальной форме (2) где 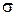– удельная электропроводность меди, – удельная тепловая мощность тока. Из формул (1) и (2) для напряженности электрического поля в проводнике следует:
а) – ? б) – ? в) - ?

В/м.

б) из выражения (1) для плотности тока имеем

А·м^-2.

в) скорость упорядоченного движения электронов и плотность тока связана соотношением

, (3)

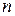где – заряд электрона; – концентрация свободных электронов. Учитывая, что на каждый атом меди приходится один свободный электрон, для концентрации свободных электронов получается

, (4)

где – число Авогадро.

Из формул (3) и (4) для скорости упорядоченного движения электронов следует

м/c

Ответ: а) В/м , б) А· , в) м/c.

ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ

3.16. Зазор между обкладками плоского конденсатора заполнен веществом с проницаемостью e = 7 и удельным сопротивлением r = 100 ГОм×м. Емкость конденсатора С = 3000 пФ. Найти силу тока утечки через конденсатор при подаче на него напряжения U = 2000 В.

(I = 9,7×10^-7A)

 

3.17. В схеме, изображенной на рисунке, e₁ = 10 В, e₂ = 20 В, e₃ = 30 В, R₁ = 1,0 Ом, R₂ = 2,0 Ом, R₃ = 3,0 Ом, R₄ = 4,0 Ом, R₅ = 5,0 Ом, R₆ = 6,0 Ом, R₇ = 7,0 Ом. Внутреннее сопротивление источников тока пренебрежимо мало. Найти силы токов I₁, I₂, I₃.

(I₁ = -1,02 A, I₂ = 0,90 A, I₃ = -0,12 A)

 

3.18. Определить заряд Q, прошедший по проводу с сопротивлением R = 3,0 Ом при равномерном нарастании напряжения на концах провода от U₀ = 2,0 B до U = 4,0 B в течение 20 с.

(Q = 20 Кл)

 

3.19. Сила тока в проводнике сопротивлением 20 Ом нарастает в течение времени Dt = 2,0 с по линейному закону от I₀ = 0 до I_max = 6,0 A. Определить количество теплоты Q, выделившееся в этом проводнике за первую секунду.

(Q = 60 Дж)

 

3.20. Концентрация электронов проводимости в меди n = 1,0·10²⁹ м^-3. Считая условия нормальными, определить среднее время между двумя столкновениями электрона с решеткой (среднее время свободного пробега). Определить среднюю длину свободного пробега электрона. Удельное сопротивление меди r = 1,7×10^-8 Ом×м.

(l = 4,7×10^{-9 м})

 

3.21. По медному проводнику сечением 0,20 мм² течет ток. Определить, какая сила действует на отдельный электрон проводимости со стороны электрического поля, если объемная плотность энергии, выделяемая в проводнике, равна 9,0×10³ Дж/м³. Определить плотность и силу тока в проводнике.

F = 20×10^-22 H; j = 7,3×10⁵ A/м²; I = 0,15 A)

 

3.22. Два источника тока, соединенные одинаковыми полюсами, с ЭДС и и внутренними сопративлениями и включены параллельно сопративлению R = 2,0 Ом. Определите силу тока через это сопративление.

(I = 0,78 A)